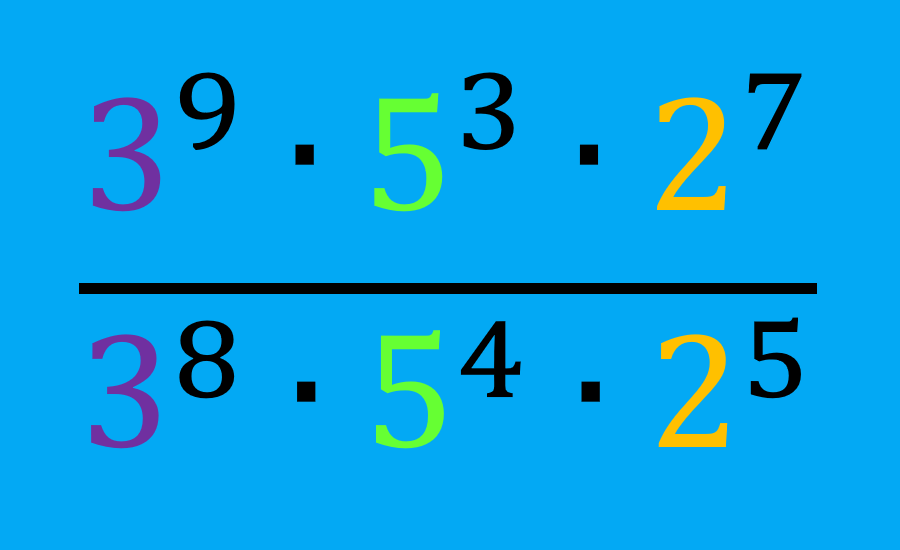The laws of exponents are some of the most important laws in algebra because they can be part of most algebraic problems. Mastering the laws of basic exponents will make your study of algebra easier and more productive.
In this article, we will learn about all the laws of exponents. We will use various examples to facilitate the mastery of these laws.
Parts of exponential expressions
Let’s start by exploring the parts of an exponential expression.
An exponential expression is made up of two parts. The first part is the base, which “carries” the exponent, which is the second part and is located in the upper right as can be seen in the illustration:
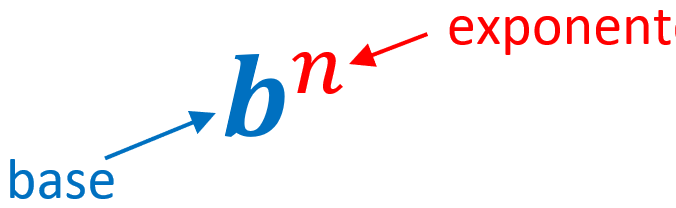
- The exponent is the number that indicates how many times the base will be multiplied by itself.
- The base is the number or variable that is being multiplied repeatedly.
For example, let’s try writing $latex 3\times 3\times 3\times 3$ in exponent notation.
The number 3 is the number that is being multiplied repeatedly, so we immediately know that 3 is the base. We note that it is written 4 times. This number indicates the number of times that the base is being multiplied, so we know that it is the exponent.
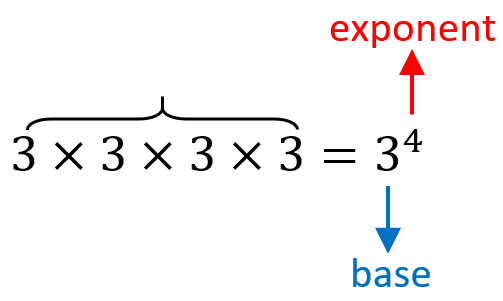
The base of an algebraic expression can also be a letter or variable. For example, if we have the variable x repeatedly multiplied by itself, we can write it in exponent notation:
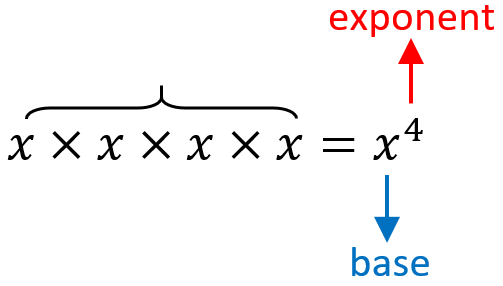
Summary of the laws of exponents
In the following laws, a and b are nonzero real numbers, and m and n are integers:
1) Law of exponent zero:
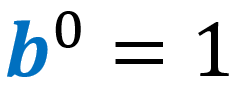
2) Law of negative exponents:
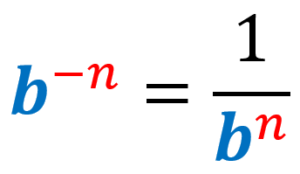
3) Law of the product of exponents:
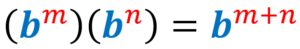
4) Law of the quotient of exponents:
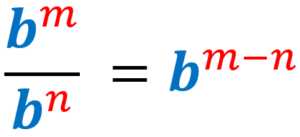
5) Law of power of a power:
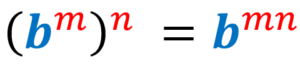
6) Law of power of a product:
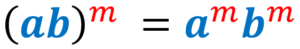
7) Law of power of a quotient:
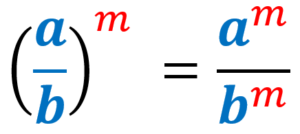
Description of the laws of exponents with examples
1) Law of exponent zero
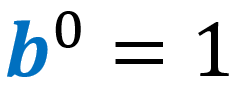
Any number raised to the power of zero is equal to 1.
EXAMPLES
- Simplify the exponential expression $latex {{4}^0}$.
Here, the base is 4 and the exponent is 0. We can apply the law of zero directly. Then, we have $latex {{4}^0}=1$.
- Simplify the exponential expression $latex {{(3x {{y}^2})}^0}$.
The base is the entire expression that is inside the parentheses. This is easier than it looks. As long as the variables x and y are different from zero, the law of zero applies and we have $latex {{(3x {{y}^2})}^0}= 1$.
2) Law of negative exponents
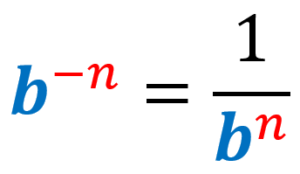
Any number that is raised to a negative exponent is not in its standard form. Therefore, we have to rewrite it. To achieve this, we move the base with the negative exponent to the opposite side of the fraction and then make the exponent positive.
EXAMPLES
- Simplify the exponential expression $latex {{2}^{-3}}$.
Here, the base is 2 and it has a negative exponent of -3. Using the law of negative exponents, we can move it to the denominator of the fraction and change the exponent from negative to positive:
$latex {{2}^{- 3}} = \frac{1}{{{2}^3}}$
$latex =\frac{1}{8}$
- Simplify the exponential expression $latex \frac{1}{{{x}^{-5}}}$.
The base with a negative exponent is in the denominator. We can move it to the numerator and change the exponent from negative to positive:
$latex \frac{1}{{{x}^{-5}}} = {{x}^{5}}$
3) Law of product of exponents
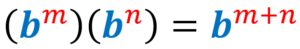
When we multiply two exponential expressions, which have the same base, we copy the base and add its exponents. Here, we assume that the base b is nonzero and the exponents m and n are integers.
EXAMPLES
- Simplify the product of the exponential expressions $latex ({{x}^3})({{x}^5})$.
Using the law of product of exponents, we simply copy the base and add the exponents:
$latex ({{x}^{{3}}})({{x}^{{5}}})={{x}^{{5+3}}}$
$latex ={{x}^{{8}}}$
- Simplify the product of the exponential expressions $latex (2{{x}^2}{{y}^3})(3{{x}^3}{{y}^4})$.
In this case, each parenthesis contains a number, the variable x, and the variable y. To solve this, we have to make sure to multiply only the terms of the same type, that is, we multiply the numbers and the variables separately:
$latex (2{{x}^{{2}}}{{y}^{{3}}})(3{{x}^{{3}}}{{y}^{{4}}})$
$latex =(2\times 3)({{x}^{{2}}}\times {{x}^{{3}}})({{y}^{{3}}}\times {{y}^{{4}}})$
$latex =6({{x}^{{2+3}}})({{y}^{{3+4}}})$
$latex =6({{x}^{{5}}})({{y}^{{7}}})$
4) Law of quotient of exponents
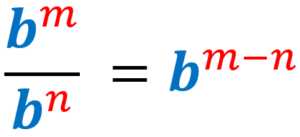
When we have a division of exponential expressions with the same base, we copy the base and subtract the exponent of the expression in the denominator from the exponent of the expression in the numerator.
Here, we assume that the base b is nonzero and that the exponents m and n are integers.
EXAMPLES
- Simplify the division of exponential expression $latex \frac{{{x}^4}}{{{x}^2}}$.
Applying the quotient rule, we copy the base and subtract the exponent below from the exponent above:
$latex \frac{{{{x}^{4}}}}{{{{x}^{2}}}}={{{x}^{4-2}}}$
$latex ={{{x}^{2}}}$
- Simplify the division of exponential expressions $latex \frac{{{x}^3}{{y}^4}}{{{x}^4}{{y}^3}}$.
We see that we have the variables x and y, therefore, we apply thelaw of quotient of exponents to each variable separately:
$latex \frac{x^3y^4}{x^4y^3}=(x^{3-4})(y^{4-3})$
$latex ={{{x}^{-1}}}{{{y}^{1}}}$
$latex =\frac{y}{x}$
5) Law of power of a power
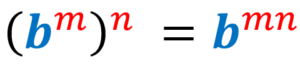
When an exponential expression is raised to a power, we copy the base and multiply the exponents. Again, we assume that the base is nonzero and the exponents are whole numbers.
EXAMPLES
- Simplify the exponential expression $latex {{\left( {{{x}^{2}}} \right)}^{3}}$.
This expression has an inner and an outer exponent. The law of power of a power tells us to copy the base and multiply the exponents:
$latex {{\left( {{{x}^{2}}} \right)}^{3}}= {{{x}^{(2)(3)}}}$
$latex ={{{x}^{6}}}$
- Simplify the exponential expression $latex {{\left( {{{x}^{3}}}{{{y}^{5}}} \right)}^{4}}$.
We apply the law of power of a power separately:
$latex {{\left( {{{x}^{3}}}{{{y}^{5}}} \right)}^{4}}={{{x}^{(3)(4)}}}{{{y}^{(4)(5)}}}$
$latex ={{{x}^{12}}}{{{y}^{20}}}$
6) Law of power of a product
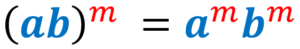
When we have the product of two or more factors raised to a power, we copy each factor and then multiply the outer exponent by its exponent. We have to do this for each factor within the parentheses. Here we assume that the bases are different from zero and the exponents are integers.
EXAMPLES
- Simplify the exponential expression $latex {{\left( {{{3}^{2}}{{x}^{3}}{{y}^{4}}} \right)}^{3}}$.
Here we have three factors each with exponents. We simply have to copy each factor and multiply its exponent by the outer exponent:
$latex {{\left( {{{3}^{2}}{{x}^{3}}{{y}^{4}}} \right)}^{3}}=({{{3}^{(2)(3)}}{{x}^{(3)(3)}}{{y}^{(4)(3)}}})$
$latex ={{{3}^{6}}{{x}^{9}}{{y}^{12}}}$
7) Law of power of a quotient
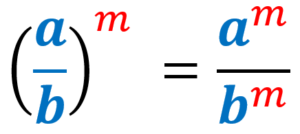
When a quotient is raised to a power, we copy the factor into the numerator and multiply its exponent by the outer exponent. Then, we do the same with the factor in the denominator. We assume that the bases are different from zero and that the exponents are integers.
EXAMPLES
- Simplify the exponential expression $latex {{\left( {\frac{{{{x}^{3}}}}{{{{y}^{5}}}}} \right)}^{4}}$.
Using the law of power of a quotient of exponents, we copy the bases in the numerator and the denominator and multiply their exponents by the outer exponent:
$latex {{\left( {\frac{{{{x}^{3}}}}{{{{y}^{5}}}}} \right)}^{4}}={\frac{{{{x}^{(3)(4)}}}}{{{{y}^{(5)(4)}}}}}$
$latex ={\frac{{{{x}^{12}}}}{{{{y}^{20}}}}}$
See also
Interested in learning more about exponents? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
