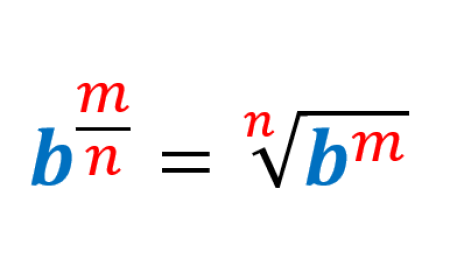Fractional exponent exercises can be solved using the fractional exponent rule. This rule indicates the relationship between powers and radicals. The denominator of a fractional exponent is written as a radical of the expression and the numerator is written as the exponent.
Here, we will see a brief summary of fractional exponents in algebraic expressions. We will also look at various fractional exponent problems to learn how to solve these types of problems.
Summary of fractional exponents
A fractional exponent is a technique for expressing powers and roots together. The general form of a fractional exponent is:
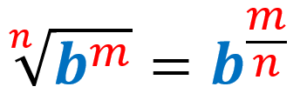
We can define the following terms:
- Radicand: The radicand is the expression under the sign √. In the expression above, the radicand is $latex {{b}^m}$.
- Index: The index or also known as the order of the radical, is the number that indicates which root is being applied. In the expression above, the index is n.
- Base: The base is the number to which the root or power applies. In this case, the base is b.
- Power: Power indicates repeated multiplication of the base by itself. In the expression above, the power is m.
Radical form to fractional exponent
To transform from radical form to fractional exponent, we have to use the fractional exponent rule inversely.
We can form a fractional exponent where the numerator is the exponent to which the base is raised and the denominator is the index of the radical. That is, we use the following relationship:
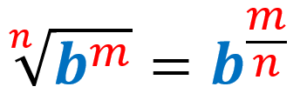
Fractional exponents – Examples with answers
EXAMPLE 1
Simplify the expression $latex {{3}^{\frac{3}{2}}}$.
Solution
The fractional exponent rule tells us that $latex {{b}^{\frac{m}{n}}}=\sqrt[n]{{{b}^m}}$. Therefore, we write 3 to the power of 3 and then we take the square root of this:
$latex 3^{\frac{3}{2}}=\sqrt[2]{3^3}$
Now, we simplify the expression by applying the exponent of 3:
$latex \sqrt[2]{3^3}=\sqrt[2]{27}$
We can simplify as follows:
$latex \sqrt[2]{27}=\sqrt[2]{9 \times 3}$
$latex =3\sqrt{3}$
EXAMPLE 2
Simplify the expression $latex {{4}^{\frac{2}{3}}}$.
Solution
Now, we have to write 4 raised to the power of 2 and we have to take the cube root of that expression:
$latex 4^{\frac{2}{3}}=\sqrt[3]{4^2}$
We simplify by applying the exponent:
$latex \sqrt[3]{4^2}=\sqrt[3]{16}$
We can simplify by rewriting 16 as 8 × 2:
$latex \sqrt[3]{16}=\sqrt[3]{8\times 2}$
The cube root of 8 is 2, so we have:
$latex \sqrt[3]{8\times 2}=2\sqrt[3]{2}$
EXAMPLE 3
Simplify the expression $latex {{-2}^{\frac{4}{3}}}{{x}^{\frac{2}{3}}}$.
Solution
Here we have a number and a variable. Raise -2 to the fourth power and take its cube root and square x and take its cube root:
$latex -2^{\frac{4}{3}}x^{\frac{2}{3}}=\sqrt[3]{(-2)^4}\sqrt[3]{x^2}$
We can apply the exponent to -2 to simplify:
$latex \sqrt[3]{(-2)^4}\sqrt[3]{x^2}=\sqrt[3]{16}\sqrt[3]{x^2}$
Similar to the previous problem, we can simplify by rewriting 16 as 8 × 2:
$latex \sqrt[3]{16}=\sqrt[3]{8\times 2}$
$latex =2\sqrt[3]{2}$
Therefore, we have:
$latex \sqrt[3]{16}\sqrt[3]{x^2}=2\sqrt[3]{2}\sqrt[3]{x^2}$
Now, we can combine the cube roots to simplify:
$latex 2\sqrt[3]{2}\sqrt[3]{x^2}=2\sqrt[3]{2x^2}$
EXAMPLE 4
Simplify the expression $latex {{6}^{\frac{3}{2}}}{{x}^{\frac{5}{2}}}$.
Solution
We write 6 cubed and take its square root. We write to the x raised to the fifth and take its square root:
$latex 6^{\frac{3}{2}}x^{\frac{5}{2}}=\sqrt{6^3}\sqrt{x^5}$
We simplify 6 cubed:
$latex \sqrt{6^3}\sqrt{x^5}=\sqrt{216}\sqrt{x^5}$
It is possible to simplify by writing to 216 as 36 × 6:
$latex \sqrt{216}=\sqrt{36\times 6}$
$latex =6\sqrt{6}$
Therefore, we have:
$latex \sqrt{216}\sqrt{x^5}=6\sqrt{6}\sqrt{x^5}$
Combining the square roots, we have:
$latex 6\sqrt{6}\sqrt{x^5}=6\sqrt{6x^5}$
EXAMPLE 5
Simplify the expression $latex {{4}^{-\frac{3}{2}}}{{x}^{\frac{1}{2}}}$.
Solution
In this case, we have a negative exponent. Remember that a negative exponent can be transformed to positive by taking the reciprocal of the base. Therefore, we have:
$latex {{4}^{-\frac{3}{2}}}{{x}^{\frac{1}{2}}}=\frac{{{x}^{\frac{1}{2}}}}{{{4}^{\frac{3}{2}}}}$
Now, we cube 4 and take its square root and take the square root of the x:
$latex \frac{{{x}^{\frac{1}{2}}}}{{{4}^{\frac{3}{2}}}}=\frac{\sqrt{x}}{\sqrt{{{4}^3}}}$
We can apply the exponent to 4 to simplify:
$latex \frac{\sqrt{x}}{\sqrt{{{4}^3}}}=\frac{\sqrt{x}}{\sqrt{64}}$
Now, we can take the square root of 64:
$latex \frac{\sqrt{x}}{\sqrt{64}}=\frac{\sqrt{x}}{8}$
EXAMPLE 6
Simplify the expression $latex {{12}^{-\frac{2}{3}}}{{x}^{\frac{3}{5}}}$.
Solution
We start transforming the exponent to positive by taking the reciprocal of the base. Therefore, we have:
$latex {{12}^{-\frac{2}{3}}}{{x}^{\frac{3}{5}}}=\frac{{{x}^{\frac{3}{5}}}}{{{12}^{\frac{2}{3}}}}$
Now, we square 12 and take its cube root. We cube x and take its fifth root:
$latex \frac{{{x}^{\frac{3}{5}}}}{{{12}^{\frac{2}{3}}}}=\frac{\sqrt[5]{{{x}^3}}}{\sqrt[3]{{{12}^2}}}$
We apply the exponent to 12:
$latex \frac{\sqrt[5]{{{x}^3}}}{\sqrt[3]{{{12}^2}}}=\frac{\sqrt[5]{{{x}^3}}}{\sqrt[3]{144}}$
We can write 144 as 8×18 and take the cube root of 8:
$latex \frac{\sqrt[5]{{{x}^3}}}{\sqrt[3]{144}}=\frac{\sqrt[5]{{{x}^3}}}{\sqrt[3]{8\times 18}}$
$latex =\frac{\sqrt[5]{{{x}^3}}}{2\sqrt[3]{18}}$
EXAMPLE 7
Simplify the expression $latex {{x}^{{\frac{1}{2}}}}{{y}^{{\frac{2}{3}}}}$.
Solution
We simply apply the rule of fractional exponents to form radicals:
$latex {{x}^{{\frac{1}{2}}}}{{y}^{{\frac{2}{3}}}}=\sqrt{x}~\sqrt[3]{{{{y}^{2}}}}$
EXAMPLE 8
Simplify the expression $latex {{81}^{{\frac{1}{4}}}}{{x}^{{\frac{1}{2}}}}$
Solution
Again, we just have to apply the rule of fractional exponents to form radicals and then we simplify:
$latex {{81}^{{\frac{1}{4}}}}{{x}^{{\frac{3}{2}}}}=\sqrt[4]{{81}}~\sqrt{{{{x}^{3}}}}$
$latex =3~\sqrt{{{{x}^{3}}}}$
EXAMPLE 9
Simplify the expression $latex {{4}^{{-\frac{1}{2}}}}{{x}^{{-\frac{1}{2}}}}$.
Solution
Here, we have negative exponents, so we start by transforming negative exponents to positive using the negative exponents rule:
$latex {{4}^{{-\frac{1}{2}}}}{{x}^{{-\frac{1}{2}}}}=\frac{1}{{{{4}^{{\frac{1}{2}}}}{{x}^{{\frac{1}{2}}}}}}$
Now, we use the fractional exponent rule and simplify:
$latex =\frac{1}{{\sqrt{4}~\sqrt{x}}}$
$latex =\frac{1}{{2~\sqrt{x}}}$
EXAMPLE 10
Simplify the expression $$\frac{{{{{16}}^{{-\frac{1}{2}}}}~{{y}^{{-\frac{1}{3}}}}}}{{{{x}^{{-\frac{1}{2}}}}~}}$$
Solution
We have negative exponents, so we start with the negative exponents rule:
$$\frac{{{{{16}}^{{-\frac{1}{2}}}}~{{y}^{{-\frac{1}{3}}}}}}{{{{x}^{{-\frac{1}{2}}}}~}}=\frac{{{{x}^{{\frac{1}{2}}}}~}}{{{{{16}}^{{\frac{1}{2}}}}~{{y}^{{\frac{1}{3}}}}~}}$$
Now, we use the fractional exponent rule and simplify:
$latex =\frac{{\sqrt{x}}}{{\sqrt{{16}}~\sqrt[3]{y}}}$
$latex =\frac{{\sqrt{x}}}{{4~\sqrt[3]{y}}}$
Fractional exponents – Practice problems
See also
Interested in learning more about exponents? Take a look at these pages: