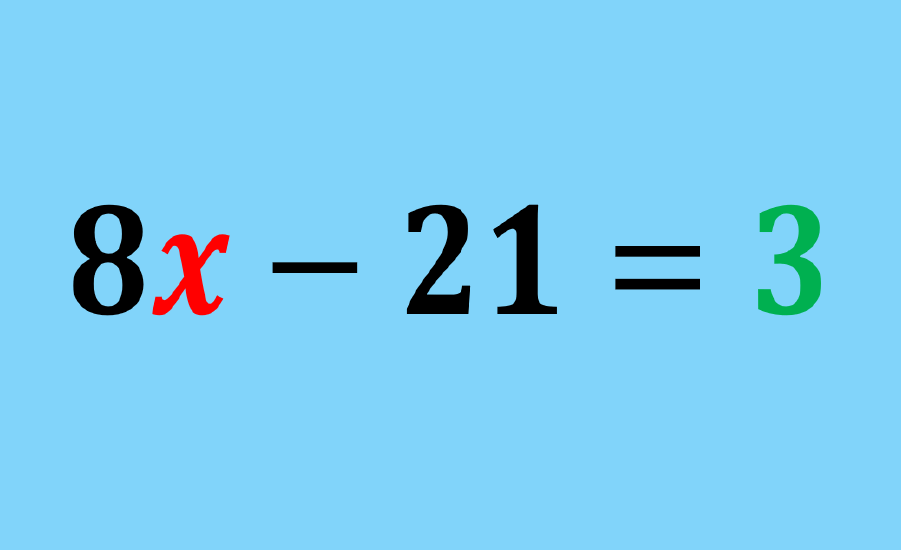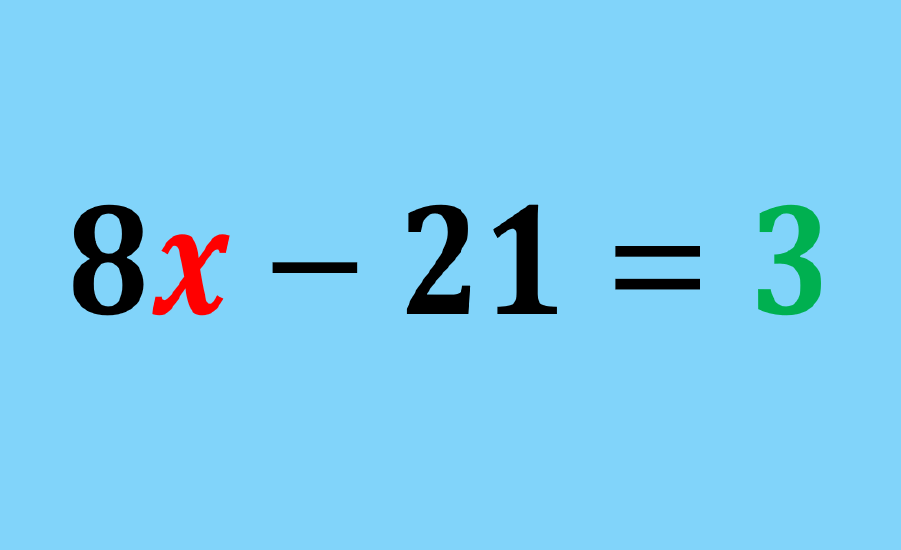First-degree equations can be solved by applying different operations to both sides of the equal sign so that we simplify the equation and solve for the variable.
In this article, we will look at a summary of solving first-degree equations. In addition, we will look at several examples with answers and practice problems.
Summary of first-degree equations
Recall that first-degree equations are equations in which all variables have a maximum exponent of 1. For example, the equations $latex 3x+2=6$ and $latex 4x+3=2x-1$ are first degree equations.
To solve first-degree equations, we remember that we can apply any operation to the equation as long as we perform that operation on both sides of the equal sign. We can follow the following steps to solve first-degree equations:
Step 1: Remove grouping signs and combine like terms.
Step 2: Isolate the terms with variables on one side of the equation.
Step 3: Use multiplication and division to solve for the variable entirely and to find its value.
First-degree equations – Examples with answers
EXAMPLE 1
Solve the equation $latex 4x+2=10$.
Solution
Step 1: Simplify: We do not have grouping signs or like terms.
Step 2: Solve for the variable: We use subtraction to solve for the variable:
$latex 4x+2=10$
$latex 4x+2-2=10-2$
$latex 4x=8$
Step 3: Solve: We use division to solve:
$latex 4x=8$
$$\frac{4}{4}x=\frac{8}{4}$$
$latex x=2$
EXAMPLE 2
Find the value of x in the equation $latex 5x-6=15-2x$.
Solution
Step 1: Simplify: We do not have grouping signs or like terms.
Step 2: Isolate the variable: We use sums to solve for the variable:
$latex 5x-6=15-2x$
$latex 5x-6+6=15-2x+6$
$latex 5x=21-2x$
$latex 5x+2x=21-2x+2x$
$latex 7x=21$
Step 3: Solve: We divide by 7 to solve:
$latex 7x=21$
$$\frac{7}{7}x=\frac{21}{7}$$
$latex x=3$
EXAMPLE 3
Find the value of x in the equation $latex 4(2x+4)=-8$.
Solution
Step 1: Simplify: We expand the parentheses:
$latex 4(2x+4)=-8$
$latex 8x+16=-8$
Step 2: Isolate the variable: We use subtraction to solve for the variable:
$latex 8x+16=-8$
$latex 8x+16-16=-8-16$
$latex 8x=-24$
Step 3: Solve: We divide by 8 to solve:
$latex 8x=-24$
$$\frac{8}{8}x=\frac{-24}{8}$$
$latex x=-3$
EXAMPLE 4
Solve the equation $latex 2(4x-11)=3(2x-4)$.
Solution
Step 1: Simplify: We expand the parentheses on both sides:
$latex 2(4x-11)=3(2x-4)$
$latex 8x-22=6x-12$
Step 2: Isolate the variable: We use addition and subtraction to solve for the variable:
$latex 8x-22+22=6x-12+22$
$latex 8x=6x+10$
$latex 8x-6x=6x+10-6x$
$latex 2x=10$
Step 3: Solve: We divide by 2 to solve:
$latex 2x=10$
$$\frac{2}{2}x=\frac{10}{2}$$
$latex x=5$
EXAMPLE 5
Solve the equation $latex 5(x-2)-3=4(2x+3)-4x$.
Solution
Step 1: Simplify: We expand the parentheses on both sides and combine like terms:
$latex 5(x-2)-3=4(2x+3)-4x$
$latex 5x-10-3=8x+12-4x$
$latex 5x-13=4x+12$
Step 2: Isolate the variable: We solve using addition and subtraction:
$latex 5x-13+13=4x+12+13$
$latex 5x=4x+25$
$latex 5x-4x=4x+25-4x$
$latex x=25$
Step 3: Solve: In this case, we no longer have to divide:
$latex x=25$
EXAMPLE 6
Solve the equation $latex \frac{5-2x}{3}=\frac{-x+7}{6}$.
Solution
Step 1: Simplify: We multiply the entire equation by 6 to eliminate the fractions:
$$\frac{5-2x}{3}=\frac{-x+7}{6}$$
$latex 2(5-2x)=-x+7$
$latex 10-4x=-x+7$
Step 2: Isolate the variable: We solve using addition and subtraction:
$latex 10-4x-10=-x+7-10$
$latex -4x=-x-3$
$latex -4x+x=-x-3+x$
$latex -3x=-3$
Step 3: Solve: We divide by -3 to solve:
$$\frac{-3}{-3}x={-3}{-3}$$
$latex x=1$
EXAMPLE 7
Solve the equation $latex 4(2x-5)=\frac{x-1}{2}+3$.
Solution
Step 1: Simplify: We multiply the entire equation by 2 to eliminate the fractions. Then we remove the parentheses and combine like terms:
$$4(2x-5)=\frac{x-1}{2}+3$$
$latex 8(2x-5)=x-1+6$
$latex 16x-40=x+5$
Step 2: Isolate the variable: We solve using addition and subtraction:
$latex 16x-40+40=x+5+40$
$latex 16x=x+45$
$latex 16x-x=x+45-x$
$latex 15x=45$
Step 3: Solve: We divide by 15 to solve:
$$\frac{15}{15}x=\frac{45}{15}$$
$latex x=3$
EXAMPLE 8
Find the value of x in the equation: $latex \frac{4x-9}{3}+2=3(x-2)$.
Solution
Step 1: Simplify: We can multiply both sides of the equation by 3. Also, we expand the parentheses and combine like terms:
$$\frac{4x-9}{3}+2=3(x-2)$$
$latex 4x-9+6=9(x-2)$
$latex 4x-3=9x-18$
Step 2: Isolate the variable: We add 3 and subtract 9x from both sides:
$latex 4x-3+3=9x-18+3$
$latex 4x=9x-15$
$latex 4x-9x=9x-15-9x$
$latex -5x=-15$
Step 3: Solve: We divide both sides by -5:
$$\frac{-5x}{-5}=\frac{-15}{-5}$$
$latex x=3$
EXAMPLE 9
Solve the equation $latex 10(2w-5)=2w+2(w+1)$ and find the value of w.
Solution
Step 1: Simplify: We just need to expand the parentheses and combine like terms:
$latex 10(2w-5)=2w+2(w+1)$
$latex 20w-50=2w+2w+2$
$latex 20w-50=4w+2$
Step 2: Isolate the variable: We add 50 and subtract 4w from both sides:
$latex 20w-50=4w+2$
$latex 20w-50+50=4w+2+50$
$latex 20w=4w+52$
$latex 20w-4w=4w+52-4w$
$latex 16w=52$
Step 3: Solve: We divide both sides by 16 and simplify the fraction:
$$\frac{16w}{16}=\frac{52}{16}$$
$latex x=\frac{13}{4}$
EXAMPLE 10
Solve the equation $latex 2\left( \frac{x+2}{4}\right)+2=\frac{3x}{4}+2$ and find the value of x.
Solution
Step 1: Simplify: We multiply the 2 in the fraction on the left-hand side to simplify it, then we multiply the entire equation by 4 to remove the fractions and combine like terms:
$$2\left( \frac{x+2}{4}\right)+2=\frac{3x}{4}+2$$
$$\frac{x+2}{2}+2=\frac{3x}{4}+2$$
$latex 2(x+2)+8=3x+8$
$latex 2x+4+8=3x+8$
$latex 2x+12=3x+8$
Step 2: Isolate the variable: We subtract 12 and 3x from both sides:
$latex 2x+12-12=3x+8-12$
$latex 2x=3x-4$
$latex 2x-3x=3x-4-3x$
$latex -x=-4$
Step 3: Solve: We divide both sides by -1:
$$\frac{-x}{-1}=\frac{-4}{-1}$$
$latex x=4$
First-degree equations – Practice problems
Find the value of t en la equation $latex \frac{x+3}{2}=\frac{x+6}{4}+\frac{1}{2}$.
Write the answer in the input box.
See also
Interested in learning more about solving equations? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
