To solve linear equations with fractions, we have to multiply the entire equation by the least common multiple to eliminate the fractions and then use the conventional method of solving first-degree equations.
In this article, we will look at several examples with answers to master this topic and we will also look at some practice problems and practice what we have learned.
ALGEBRA
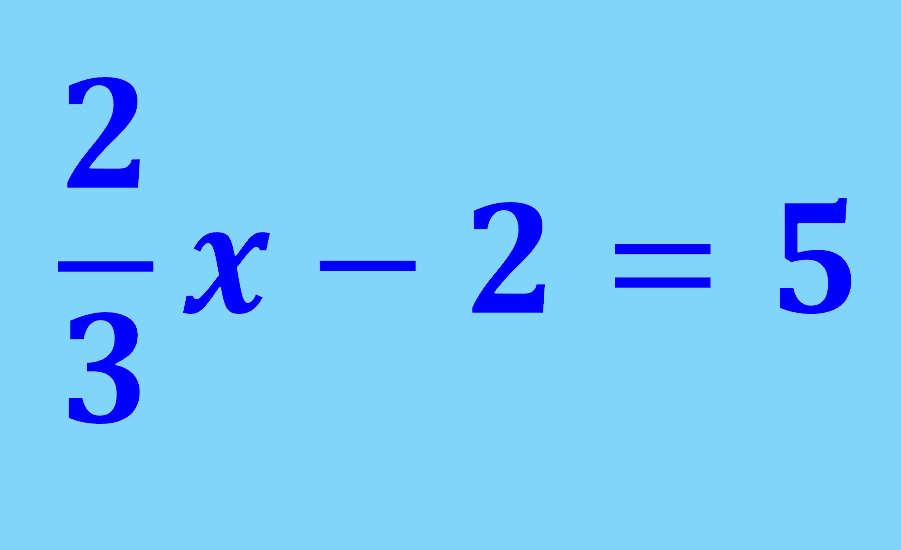
Relevant for…
Exploring linear equations with fractions examples and practice problems.
ALGEBRA
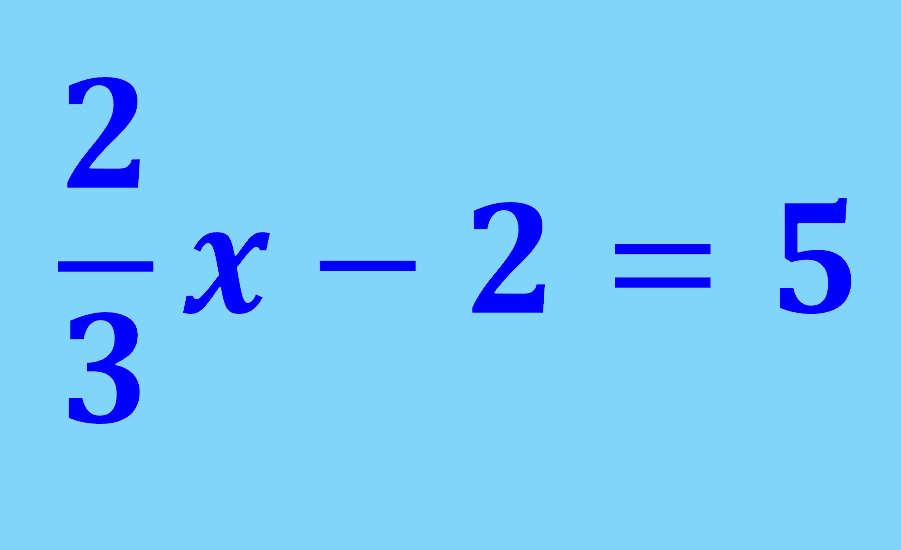
Relevant for…
Exploring linear equations with fractions examples and practice problems.
Summary of linear equations with fractions
Recall that, for an equation to be of the first degree, all the variables in the equation must have a maximum power of 1. For example, the equations $latex \frac{1}{3}x+2=6$ and $latex \frac{3}{2}x=\frac{1}{2}x+10$ are linear equations with fractions. We can solve linear equations with fractions with the following steps:
Step 1: Remove the fractions: We multiply the entire equation by the least common multiple to remove the fractions.
Step 2: Simplify: We remove the parentheses and other grouping signs and combine like terms.
Step 3: Solve for the variable: We use addition and subtraction to move the variable to only one side of the equation.
Step 4: Solve: We use multiplication and division to solve for the variable completely.
Solved examples of linear equations with fractions
EXAMPLE 1
Solve the equation
$$\frac{x}{3}+4=6$$
Solution
Step 1: Remove the fractions: We multiply the entire equation by 3:
$$\frac{x}{3}+4=6$$
$latex x+4(3)=6(3)$
$latex x+12=18$
Step 2: Simplify: We have nothing to simplify.
Step 3: Solve for the variable: We subtract 12 from both sides of the equation:
$latex x+12-12=18-12$
$latex x=6$
Step 4: Solve: We have already got the answer:
$latex x=6$
EXAMPLE 2
Find the value of $latex x$ in the equation
$$\frac{1}{2}x+4(x+2)=14-2x+20$$
Solution
1. Simplify:
- Remove the parentheses: $latex \frac{1}{2}x+4x+8=14-2x+20$.
- Simplify the fractions by multiplying by 2: $latex x+8x+16=28-4x+40$.
- Combine like terms: $latex 9x+16=68-4x$.
2. Isolate the variable: move the 16 to the right and the -4x to the left:
$latex 9x+16-16=68-4x-16$
$latex 9x=52-4x$
$latex 9x+4x=52-4x+4x$
$latex 13x=52$
3. Apply different operations to isolate the $latex x$: divide both sides by 13:
$$\frac{13}{13}x=\frac{{52}}{13}$$
$$x=\frac{{52}}{13}=4$$
4. Verify your solution: substitute the value in the original equation:
$$\frac{1}{2}(4)+4(4+2)=14-2(4)+20$$
$latex 2+16+8=14-8+20$
$latex 26=26$
This is true
Answer: $latex x=4$
EXAMPLE 3
Find the value of x in the equation
$$\frac{x+1}{2}+2=4$$
Solution
Step 1: Remove the fractions: We multiply the entire equation by 2:
$$\frac{x+1}{2}+2=4$$
$latex x+1+2(2)=4(2)$
$latex x+1+4=8$
Step 2: Simplify: We combine like terms:
$latex x+1+4=8$
$latex x+5=8$
Step 3: Solve for the variable: We subtract 5 from both sides:
$latex x+5-5=8-5$
$latex x=3$
Step 4: Solve: We have already got the answer:
$latex x=3$
EXAMPLE 4
Find the value of x in the equation
$$\frac{2x+5}{3}+2x=7$$
Solution
Step 1: Remove the fractions: We multiply the entire equation by 3:
$$\frac{2x+5}{3}+2x=7$$
$latex 2x+5+2x(3)=7(3)$
$latex 2x+5+6x=21$
Step 2: Simplify: We combine like terms:
$latex 2x+5+6x=21$
$latex 8x+5=21$
Step 3: Solve for the variable: We subtract 5 from both sides:
$latex 8x+5-5=21-5$
$latex 8x=16$
Step 4: Solve: We divide both sides by 8:
$$\frac{8x}{8}=\frac{16}{8}$$
$latex x=2$
EXAMPLE 5
Find the value of $latex x$ in the equation
$$\frac{1}{3}x+4+\frac{1}{2}x=9$$
Solution
1. Simplify:
- There are no parentheses.
- Simplify the fractions: multiply by 6: $latex 2x+24+3x=54$.
- Combine like terms: $latex 5x+24=54$.
2. Isolate the variable: move the 24 to the right:
$latex 5x+24-24=54-24$
$latex 5x=30$
3. Apply different operations to isolate the $latex x$: divide both sides by 5:
$$\frac{5}{5}x=\frac{{30}}{5}$$
$$x=\frac{{30}}{5}=6$$
4. Verify your solution: substitute the value in the original equation:
$$\frac{1}{3}(6)+4+\frac{1}{2}(6)=9$$
$latex 2+4+3=9$
$latex 9=9$
This is true
Answer: $latex x=6$.
EXAMPLE 6
Find the value of x in the equation
$$\frac{3x-4}{4}+6=2x+10$$
Solution
Step 1: Remove the fractions: We multiply the entire equation by 4:
$$\frac{3x-4}{4}+6=2x+10$$
$$3x-4+6(4)=2x(4)+10(4)$$
$latex 3x-4+24=8x+40$
Step 2: Simplify: We combine like terms:
$latex 3x-4+24=8x+40$
$latex 3x+20=8x+40$
Step 3: Solve for the variable: We subtract 20 and 8x from both sides of the equation:
$latex 3x+20-20=8x+40-20$
$latex 3x=8x+20$
$latex 3x-8x=8x+20-8x$
$latex -5x=20$
Step 4: Solve: We divide both sides by -5:
$$\frac{-5x}{-5}=\frac{20}{-5}$$
$latex x=-4$
EXAMPLE 7
Find the value of $latex x$ in the equation
$$\frac{1}{2}x+2(x+1)=\frac{1}{5}x+4+x+11$$
Solution
1. Simplify:
- Remove the parentheses: $latex \frac{1}{2}x+2x+2=\frac{1}{5}x+4+x+11$.
- Remove the fractions: multiply by 10: $$5x+20x+20=2x+40+10x+110$$
- Combine like terms: $latex 25x+20=12x+150$.
2. Isolate the variable: move the 20 to the right and the 12x to the left:
$latex 25x+20-20=12x+150-20$
$latex 25x=12x+130$
$latex 25x-12x=12x-12x+130$
$latex 13x=130$
3. Apply operations to isolate the $latex x$: divide both sides by 13:
$$\frac{13}{13}x=\frac{{130}}{13}$$
$$x=\frac{{130}}{13}=10$$
4. Verify your solution: substitute the value in the original equation:
$$\frac{1}{2}(10)+2(10+1)=\frac{1}{5}(10)+4+10+11$$
$latex 5+2(11)=2+4+10+11$
$latex 27=27$
This is true
Answer: $latex x=10$.
EXAMPLE 8
Solve the equation $latex \frac{t+5}{2}+5=\frac{t-6}{3}+10$ for t.
Solution
Step 1: Remove the fractions: We multiply the entire equation by 6:
$$\frac{t+5}{2}+5=\frac{t-6}{3}+10$$
$$3(t+5)+5(6)=2(t-6)+10(6)$$
$latex 3(t+5)+30=2(t-6)+60$
Step 2: Simplify: We expand the parentheses and combine like terms:
$latex 3(t+5)+30=2(t-6)+60$
$latex 3t+15+30=2t-12+60$
$latex 3t+45=2t+48$
Step 3: Solve for the variable: We subtract 45 and 2 t from both sides:
$latex 3t+45-45=2t+48-45$
$latex 3t=2t+3$
$latex 3t-2t=2t+3-2t$
$latex t=3$
Step 4: Solve: We already got the answer:
$latex t=3$
EXAMPLE 9
Solve the following equation
$$\frac{5x-10}{2}+5=2(2x-2)+1$$
Solution
Step 1: Remove the fractions: We multiply the entire equation by 2:
$$\frac{5x-10}{2}+5=2(2x-2)+1$$
$$5x-10+5(2)=2(2)(2x-2)+1(2)$$
$latex 5x-10+10=4(2x-2)+2$
Step 2: Simplify: We remove the parentheses and combine like terms:
$latex 5x-10+10=4(2x-2)+2$
$latex 5x-10+10=8x-8+2$
$latex 5x=8x-6$
Step 3: Solve for the variable: We subtract 8x from both sides of the equation:
$latex 5x-8x=8x-6-8x$
$latex -3x=-6$
Step 4: Solve: We divide both sides by -3:
$$\frac{-3x}{-3}=\frac{-6}{-3}$$
$latex x=2$
EXAMPLE 10
Find the value of z from the equation
$$\frac{2z+1}{3}+\frac{z-1}{2}=\frac{-3z-5}{2}-11$$
Solution
Step 1: Remove the fractions: We multiply the entire equation by 6 to eliminate all fractions:
$$\frac{2z+1}{3}+\frac{z-1}{2}=\frac{-3z-5}{2}-11$$
$$2(2z+1)+3(z-1)=3(-3z-5)-6(11)$$
$$2(2z+1)+3(z-1)=3(-3z-5)-66$$
Step 2: Simplify: We remove the parentheses and combine like terms:
$$2(2z+1)+3(z-1)=3(-3z-5)-66$$
$latex 4z+2+3z-3=-9z-15-66$
$latex 7z-1=-9z-81$
Step 3: Solve for the variable: Add 1 and 9 z from both sides of the equation:
$latex 7z-1+1=-9z-81+1$
$latex 7z=-9z-80$
$latex 7z+9z=-9z-80+9z$
$latex 16z=-80$
Step 4: Solve: We divide both sides by 16:
$$\frac{16z}{16}=\frac{-80}{16}$$
$latex x=-5$
Linear equations with fractions – Practice problems
Find the value of x in $latex \frac{2x-2}{3}+\frac{3x}{2}=-5$.
Write the answer in the input box.
See also
Interested in learning more about solving equations? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
