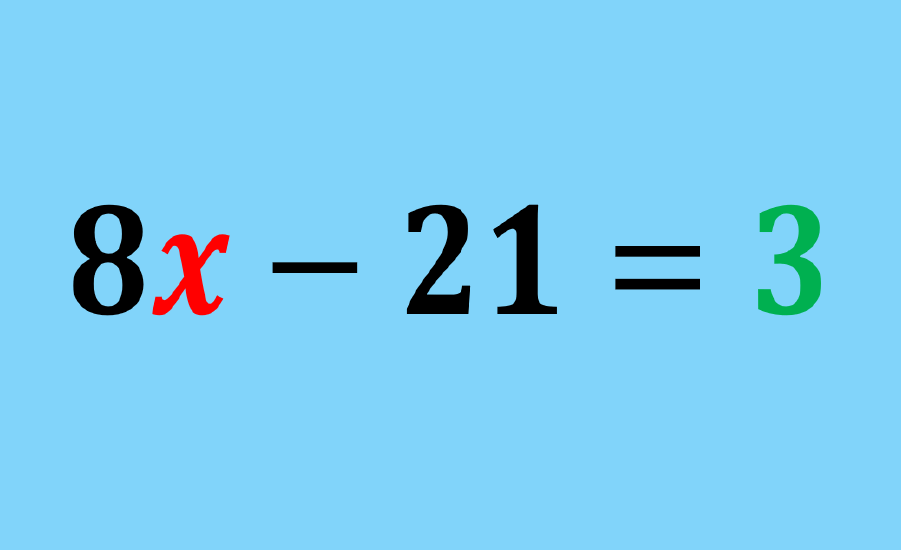Exercises of Linear Equations

Step 1: Simplify: We do not have parentheses, fractions, or like terms.

Step 2: Isolate the variable: Add 10 to both sides of the equation:

$latex 5x-10=10$

$latex 5x-10+10=10+10$

$latex 5x=20$

Step 3: Solve: We divide both sides by 5:

$$\frac{5x}{5}=\frac{20}{5}$$

$latex x=4$

Step 1: Simplify: We can combine like terms on the left-hand side of the equation:

$latex 2x-4+2x=12$

$latex 4x-4=12$

Step 2: Isolate the variable: We add 4 to both sides:

$latex 4x-4=12$

$latex 4x-4+4=12+4$

$latex 4x=16$

Step 3: Solve: We divide both sides by 4:

$$\frac{4x}{4}=\frac{16}{4}$$

$latex x=4$

Step 1: Simplify: We cannot combine like terms initially.

Step 2: Solve for the variable: Add 6 and 4t on both sides of the equation:

$latex 4t-6=10-4t$

$latex 4t-6+6=10-4t+6$

$latex 4t=16-4t$

$latex 4t+4t=16-4t+4t$

$latex 8t=16$

Step 3: Solve: Both sides of the equation are divided by 8.:

$$\frac{8t}{8}=\frac{16}{8}$$

$latex x=3$

Step 1: Simplify: We do not have parentheses, fractions, or like terms.

Step 2: Isolate the variable: We add 5 and subtract 3y from both sides:

$latex 4y-5=3y+1$

$latex 4y-5+5=3y+1+5$

$latex 4y=3y+6$

$latex 4y-3y=3y+6-3y$

$latex y=6$

Step 3: Solve: We have already got the answer:

$latex y=6$

Step 1: Simplify: We expand the parentheses:

$latex 2(2x-3)=2x-10$

$latex 4x-6=2x-10$

Step 2: Isolate the variable: We add 6 and subtract 2x from both sides:

$latex 4x-6+6=2x-10+6$

$latex 4x=2x-4$

$latex 4x-2x=2x-4-2x$

$latex 2x=-4$

Step 3: Solve: We divide both sides by 2:

$$ \frac{2x}{2}=\frac{-4}{2}$$

$latex x=-2$

Step 1: Simplify: We expand the parentheses and combine like terms:

$latex 3x-4=3(2x-2)-7$

$latex 3x-4=6x-6-7$

$latex 3x-4=6x-13$

Step 2: Isolate the variable: We add 4 and subtract 6x from both sides:

$latex 3x-4+4=6x-13+4$

$latex 3x=6x-9$

$latex 3x-6x=6x-9-6x$

$latex -3x=-9$

Step 3: Solve: We divide both sides by -3:

$$\frac{-3x}{-3}=\frac{-9}{-3}$$

$latex x=3$

Step 1: Simplify: Use the distributive property for the parenthesis and combine like terms.:

$$2t-6+3t=2(-2t+2)+8$$

$$5t-6=2(-2t+2)+8$$

$$5t-6=-4t+4+8$$

$$5t-6=-4t+12$$

Step 2: Solve for the variable: Add 6 and 4t on both sides of the equation:

$$5t-6+6=-4t+12+6$$

$latex 5t=-4t+18$

$latex 5t+4t=-4t+18+4t$

$latex 9t=18$

Step 3: Solve: Divide both sides by 9:

$$\frac{9t}{9}=\frac{18}{9}$$

$latex x=2$

Step 1: Simplify: We expand the parentheses on both sides and combine like terms:

$latex 2(t+2)-5=5(t-4)+13$

$latex 2t+4-5=5t-20+13$

$latex 2t-1=5t-7$

Step 2: Isolate the variable: We add 1 and subtract 5t from both sides:

$latex 2t-1+1=5t-7+1$

$latex 2t=5t-6$

$latex 2t-5t=5t-6-5t$

$latex -3t=-6$

Step 3: Solve: We divide both sides by -3:

$$\frac{-3t}{-3}=\frac{-6}{-3}$$

$latex x=2$

Step 1: Simplify: We multiply the entire equation by 2 to eliminate the fraction:

$$\frac{3x}{2}+4=2x+5$$

$latex 3x+4(2)=2x(2)+5(2)$

$latex 3x+8=4x+10$

Step 2: Isolate the variable: We subtract 8 and 4x from both sides:

$latex 3x+8-8=4x+10-8$

$latex 3x=4x+2$

$latex 3x-4x=4x+2-4x$

$latex -x=2$

Step 3: Solve: We divide both sides by -1:

$$\frac{-x}{-1}=\frac{2}{-1}$$

$latex x=-2$

Step 1: Simplify: We multiply the entire equation by 6 to eliminate the fractions and combine like terms:

$$\frac{x+6}{3}+4=\frac{3x-5}{2}+2x-1$$

$$2(x+6)+4(6)=3(3x-5)+2x(6)-1(6)$$

$$2x+12+24=9x-15+12x-6$$

$latex 2x+36=21x-21$

Step 2: Isolate the variable: We subtract 36 and 21x from both sides:

$latex 2x+36-36=21x-21-36$

$latex 2x=21x-57$

$latex 2x-21x=21x-57-21x$

$latex -19x=-57$

Step 3: Solve: We divide both sides by -19:

$$\frac{-19x}{-19}=\frac{-57}{-19}$$

$latex x=3$