Domain and Range of Trigonometric Functions

Domain and range of trigonometric functions (sin, cos, tan)

Sine

We can start by considering the simplest trigonometric identity:

$latex {{\sin}^2}(x)+{{\cos}^2}(x)=1$

From this identity, we can derive the following interpretations:

$latex {{\cos}^2}(x)=1-{{\sin}^2}(x)$

$latex \cos(x)=\sqrt{1-{{\sin}^2}(x)}$

We know that the cosine function is defined for real values, so the value inside the square root cannot be negative. Therefore, we can form the inequality :

$latex 1-{{\sin}^2}(x)\geq 0$

$latex {{\sin}^2}(x)\leq 1$

$latex \sin(x)\in [-1, 1]$

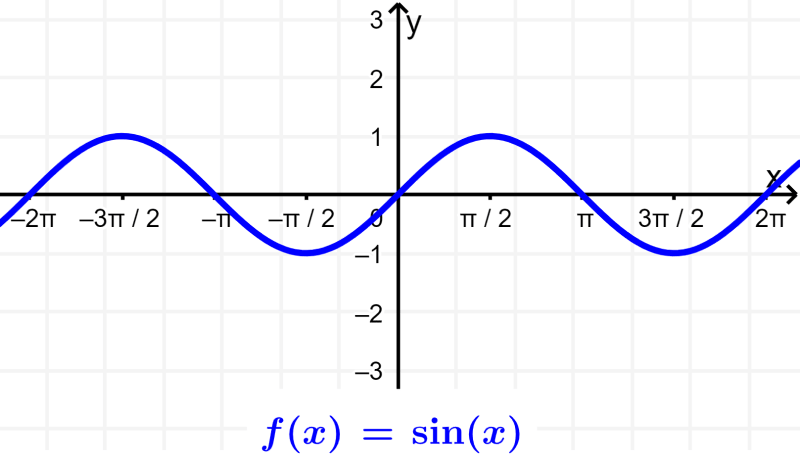
Therefore, we have already obtained the domain and range for the sine function. The domain is all the real numbers of x since we do not have any restrictions on the values of x. The range is from -1 to 1, including these values. We can check this by looking at its graph:

Cosine

Similarly, using the same methodology, we have:

$latex 1-{{\cos}^2}(x)\geq 0$

$latex {{\cos}^2}(x)\leq 1$

$latex \cos(x)\in [-1, 1]$

Therefore, the domain of the cosine function is also all the real numbers of x. The range of the cosine function is from -1 to 1, including these values. We can verify this by looking at its graph:

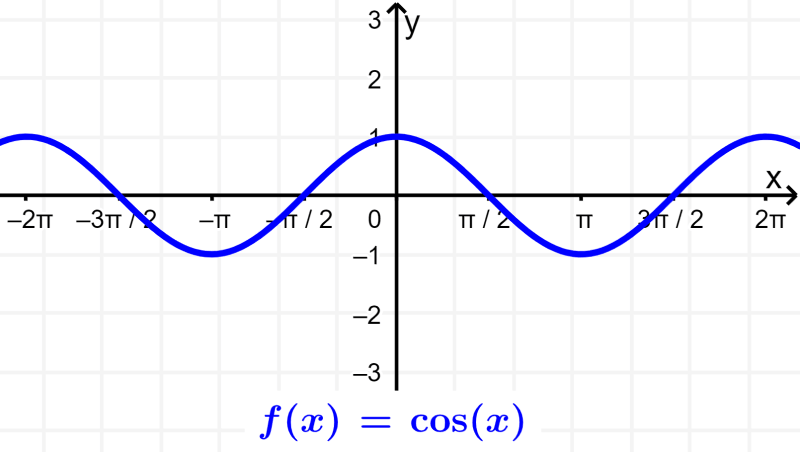
Something important to keep in mind is that the range of sine and cosine depends on the amplitude of the functions. For example, if we have $latex f(x)=5 \cos(x)$, the range is from -5 to 5.

Tangent

Now, let’s look at the function $latex f(x)= \tan(x)$. We know that $latex \tan(x)= \frac{\sin(x)}{\cos(x)}$. This means that the tangent function is defined for all values except those that make $latex \cos(x)$ equal to zero, since a fraction with denominator equal to zero is undefined.

Now, we know that $latex \cos (x)$ is zero for the angles $latex \frac{\pi}{2}, ~ \frac{3 \pi}{2}, ~ \frac{5 \pi}{ 2}$, etc.

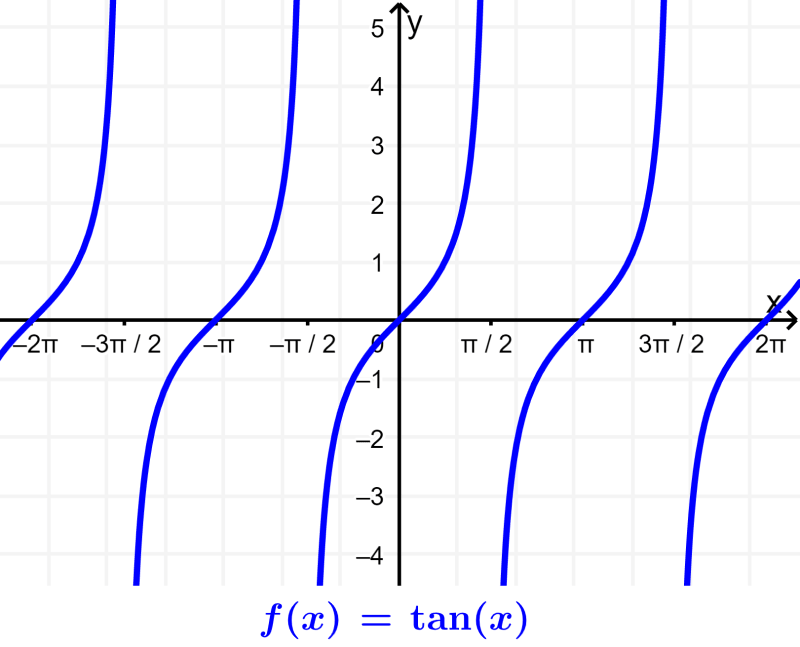
Therefore, the domain of the tangent function is $latex R- \frac{(2n+1) \pi}{2}$ and the range is all real numbers. We can see this in the graph:

---

Domain and range of functions cosec, sec and cot

Secant

We know that the secant is the reciprocal function of the cosine. Therefore, we have:

$latex \sec(x)=\frac{1}{\cos(x)}$

That means that the secant will not be defined for the points where $latex \cos(x)=0$. Therefore, the domain of $latex f(x)=\sec(x)$ will be $latex R-\frac{(2n+1)\pi}{2}$.

The range of the secant will be $latex R-(-1, 1)$. Given that $latex \cos(x)$ is located between -1 to 1, the secant can never be in this region. We can look at the graph:

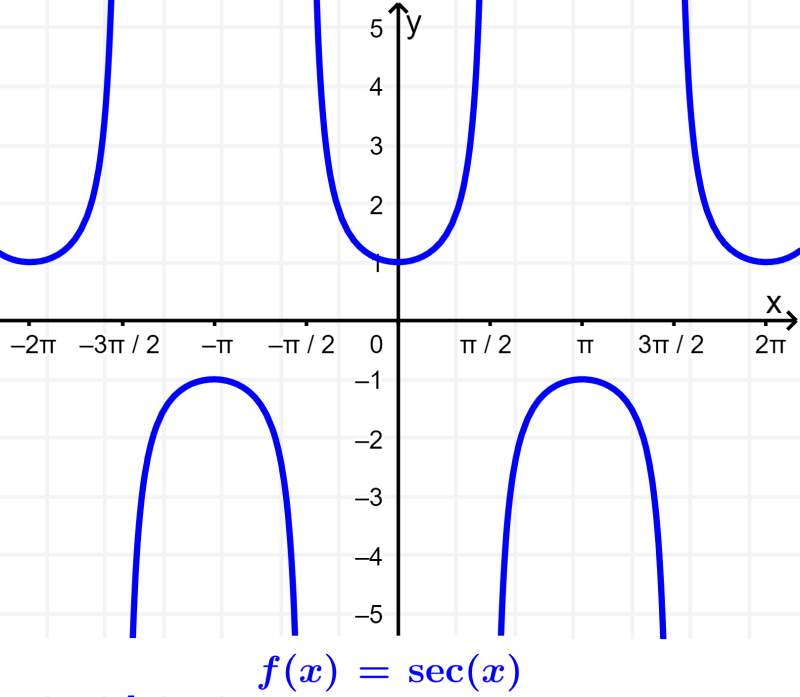
Cosecant

The cosecant is the reciprocal function of the sine. Therefore, we have:

$latex \csc(x)=\frac{1}{\sin(x)}$

We know that the cosecant will not be defined for the points where $latex \sin(x)=0$. Therefore, the domain of $latex f(x)=\csc(x)$ will be $latex R-n\pi$.

The range of the cosecant will be $latex R-(-1, 1)$. This is because $latex \sin(x)$ is between -1 to 1, so the cosecant can never be in this region. We can check it with its graph:

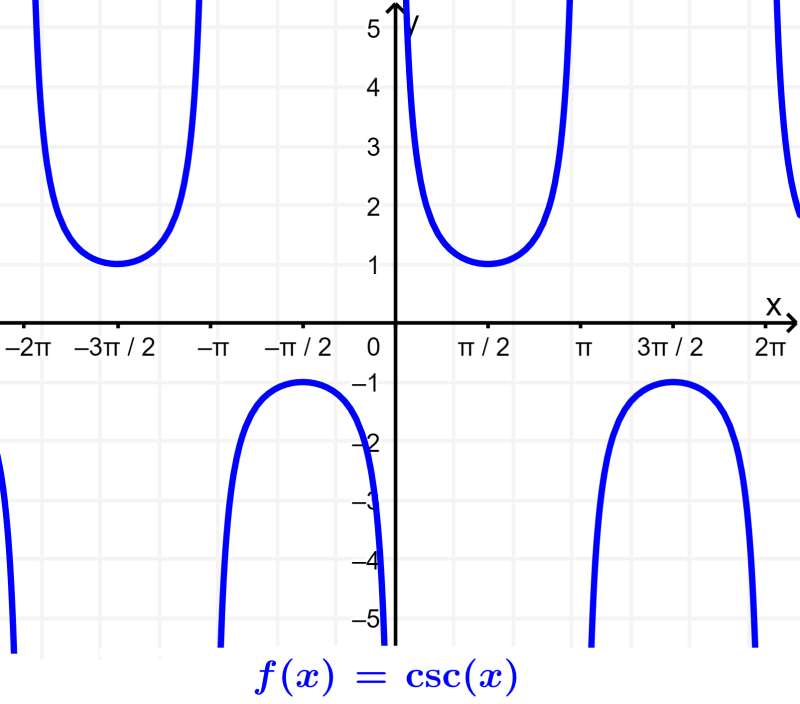
Cotangent

The cotangent is the reciprocal of the tangent. Therefore, we have:

$latex \cot(x)=\frac{1}{\tan(x)}$

The cotangent function will not be defined for the points where $latex \tan(x)=0$. Therefore, the domain of $latex f(x)=\cot(x)$ will be $latex R-n\pi$.

The range of the cotangent will be $latex R – (- 1, 1)$ the set of all real numbers because we have no restrictions. We can look at the graph:

---

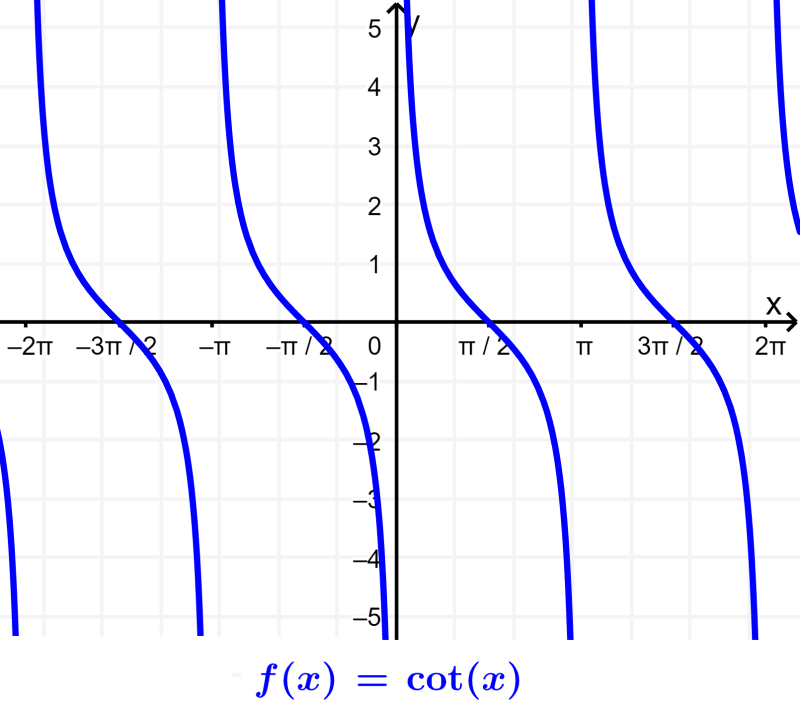
See also

Interested in learning more about the domain and range of functions? Take a look at these pages:

• Domain and Range of a Graph
• Domain and Range of Linear Functions
• Domain and Range of Quadratic Functions
• Domain and Range of Rational Functions
• Domain and Range of Exponential Functions
• Domain and Range of Logarithmic Functions