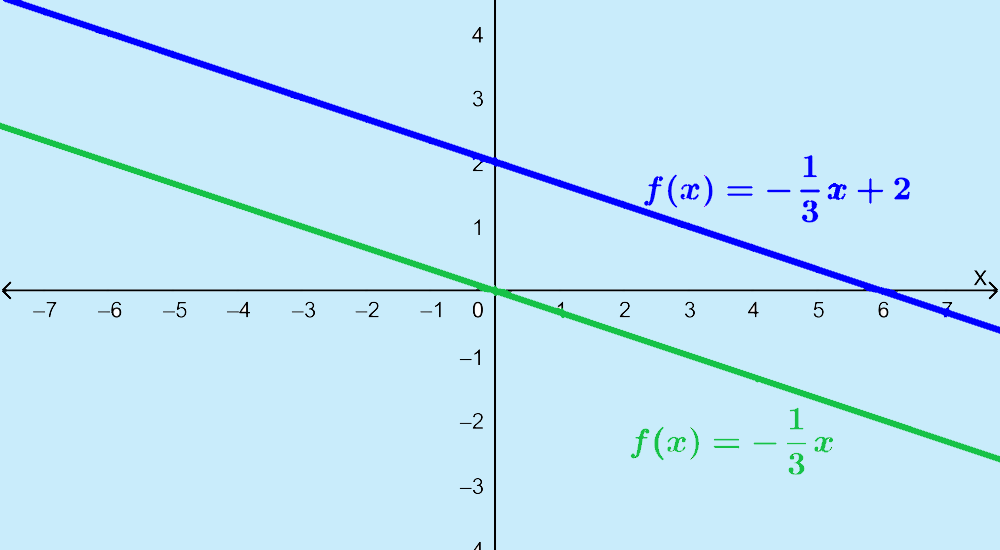The domain of linear functions is equal to the entire set of real numbers of x. This is because we do not have any restrictions on the values of x. Similarly, the range of linear functions is also the entire set of real numbers in y.
Here, we will look at more details about the range and domain of linear functions. Also, we will look at some examples that will help us to visualize the domain and range of linear functions.
What is the domain?
The domain is the set of all possible values that the independent variable can have. Generally, the domain is defined as all possible values of x.
The domain can be determined by finding values that make the function undefined and extracting those values from the domain. In most cases, this includes avoiding having denominators that are equal to zero since division by zero is undefined.
Also, we have to avoid having a negative value within a square root or other even roots as this will result in imaginary numbers.
What is the range?
The range is defined as all the possible values of the dependent variable that are obtained by using all the values of the domain as input. We can consider the range as all possible values of y.
Finding the range is a bit more complicated since we must first have knowledge about the domain. To make it easier to find the range, we can graph the function with a graphing calculator or sketch a simple graph of the function to get an idea of what its range might be.
Examples of domain and range of linear functions
To find the domain of a linear function, we identify whether we have denominators that could become zero or square roots that could contain negative values. We know that the general form of a linear function is $latex f(x)=ax+b$.
A linear function is not composed of denominators or square roots, so we do not have any restrictions on the domain of the function. That means that the domain is equal to all real numbers. This can be represented in set notation as:
$latex \{x | x \in R \}$
And in interval notation as:
$latex (- \infty, \infty)$
The graph of a linear function is a straight line. These functions have no restrictions, so they grow from “negative” infinity to “positive” infinity. That means the range is also equal to all real numbers and in set notation we have:
$latex \{y | y \in R \}$
EXAMPLE 1
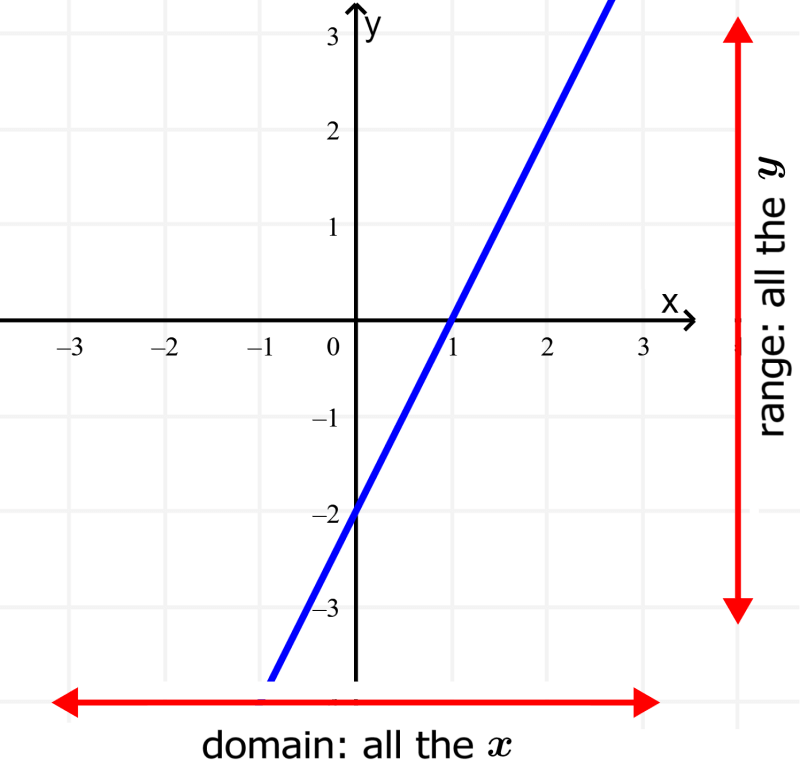
Find the domain and the range of the linear function y = 2x-2.
Solution: The first thing we can see is that we do not have square roots or denominators. This means that we will not have problems with negative numbers in square roots or zeros in denominators.
Therefore, we can easily determine that the domain is all real numbers of x. The following table shows the domain and range of this function:
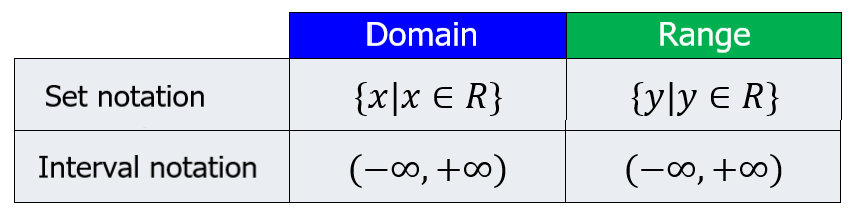
Since the graph of the function is a line, we can predict that the range is all real values of y. The line can go as high or as low as you want with no limits. We can observe this in the graph of the function:
EXAMPLE 2
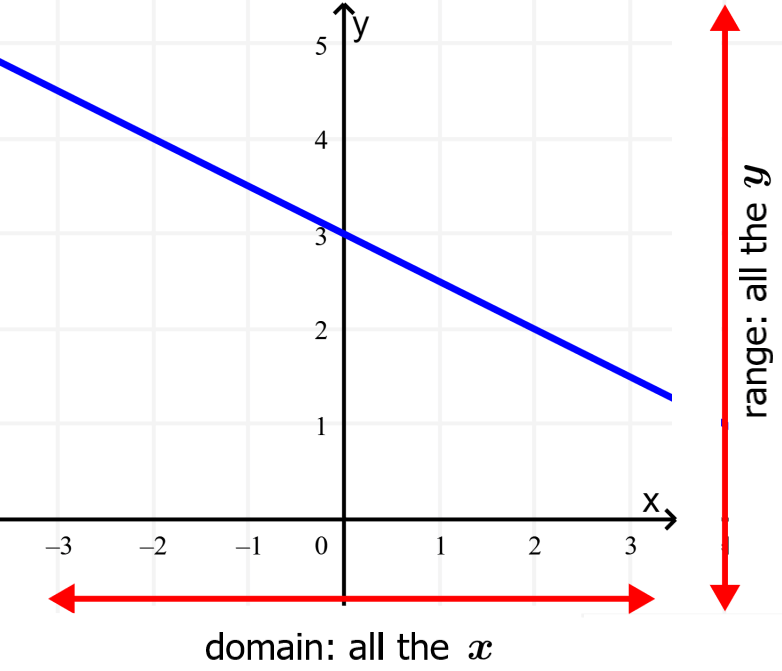
Determine the domain and range of the linear function $latex y= – \frac{1}{2}x+3$.
Solution: Similar to the previous problem, we have neither square roots nor denominators. Therefore, we know that we are not restricted to any value and the domain is all real numbers of x. This will be true of all linear functions. The following table shows the domain and range of this function:
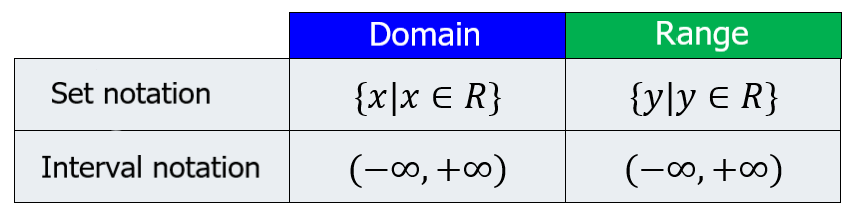
Similarly, we know that the range will be all the real values of y. In the graph of the function, we can see that the line can result in any value of y. This will always be the case for linear functions.
See also
Interested in learning more about the domain and range of functions? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
