Logarithmic functions are the inverse functions of the exponential functions. This means that their domain and range are swapped. The domain of logarithmic functions is equal to all real numbers greater or less than the vertical asymptote. The range of exponential functions is always equal to all real numbers since we have no restrictions on the output values.
Here, we will learn how to determine the domain and range of logarithmic functions. In addition, we will look at some examples with the graphs of the functions to illustrate these ideas.
How to find the domain and range of logarithmic functions?
The limits on the domain of logarithmic functions result from the fact that it is impossible to take the logarithm of a negative number. On the other hand, logarithmic functions have no limits on the range.
We can look at the graph of the “standard” logarithmic function $latex f(x)=\log(x)$:
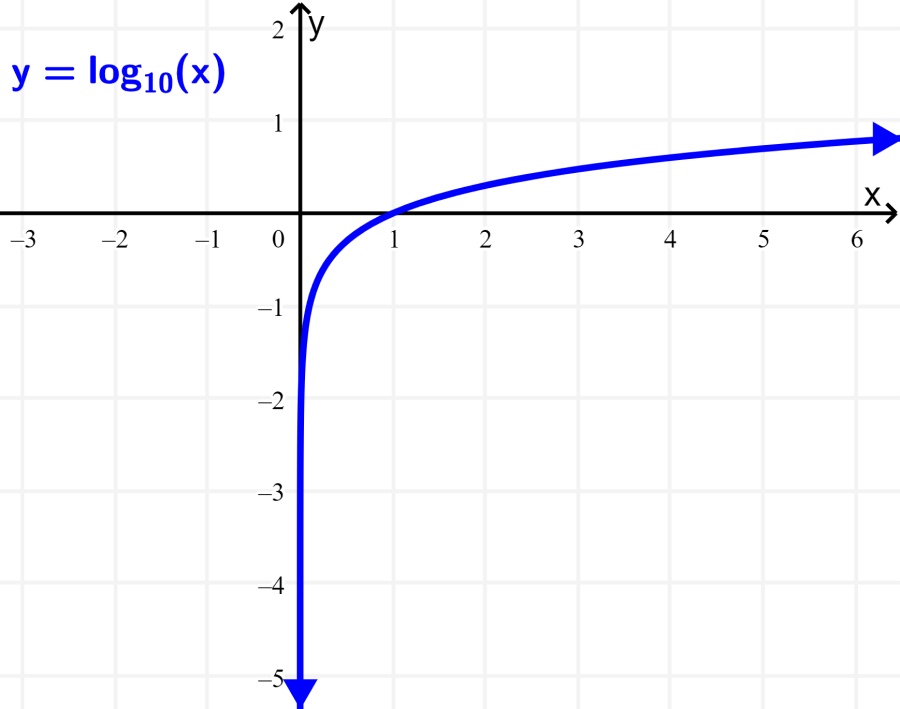
We see that the graph of the function $latex f(x)= \log(x)$ has a key point at (1, 0). From this point, the graph has an asymptote on the left that approaches $latex x=0$. Also, from the point (1, 0), the graph gradually ascends to the right with no upper bound.
By visualizing the graph, we can easily determine the domain and range. Remember that the domain is the set of all the values that the independent variable can take. Therefore, the domain of the “standard” logarithmic function is all numbers greater than 0 up to positive infinity:
The domain is $latex 0< x <+\infty$
Remember that the range is the set of all the values that the dependent variable can take. In the graph, we see that on the left side, the function goes towards negative infinity.
On the right side, we see that the function gradually ascends and goes towards positive infinity. Therefore, the range is equal to all real numbers from negative infinity to positive infinity:
The range is $latex – \infty <y <+\infty$
Now, we can determine the range and domain of other logarithmic functions by considering how the function and the graph change as we introduce various constants. We can use the following constants:
$latex y=a ~\log(x-h)+k$
Using these constants, the point (1, 0) changes to (h, k). The h represents the horizontal translation and the k represents the vertical translation.
The important thing here is that the asymptote changes with the value of h and this changes the domain. However, the range is not affected and is still all real numbers.
Examples of domain and range of logarithmic functions
EXAMPLE 1
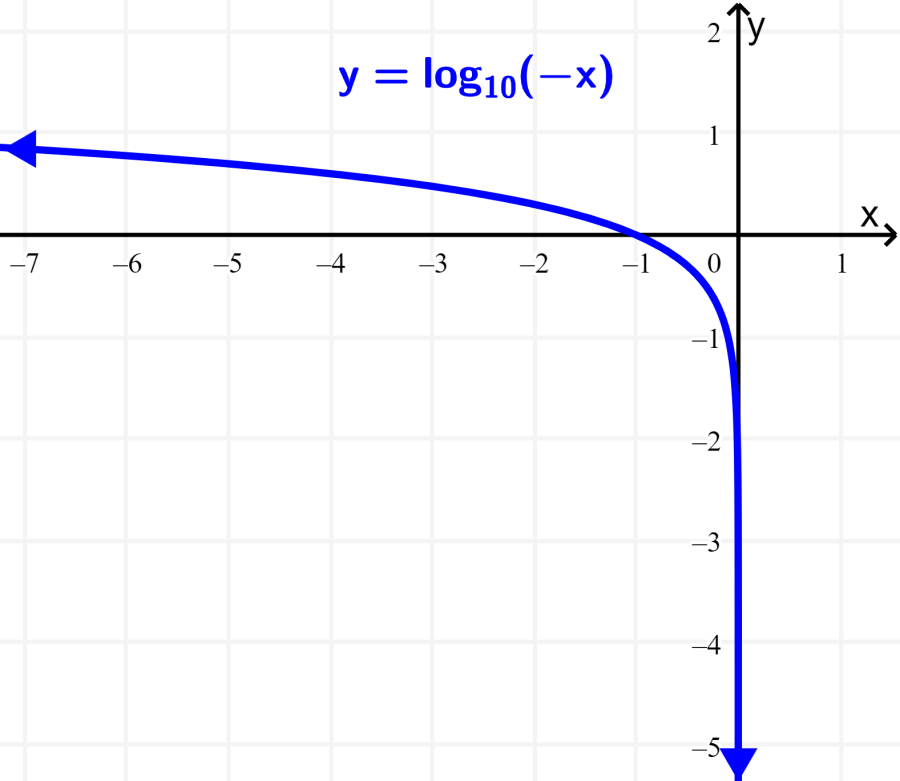
What is the domain and range of the function $latex f(x)=\log(-x)$?
Solution: This change in function produces a reflection with respect to the y-axis. Due to this reflection, the key point will be (-1, 0). From there the function will approach the asymptote down on the right-hand side and approach $latex x = 0$.
From the key point, the function will gradually rise to infinity on the left side. Therefore, the domain is from negative infinity to 0 :
Domain: $latex -\infty<x<0$
The range is still all real numbers:
Range: $latex -\infty<y<\infty$
Using interval notation, we have:
Domain: $latex (-\infty, 0)$
Range: $latex (-\infty, \infty)$
We can verify this in the graph of the function:
EXAMPLE 2
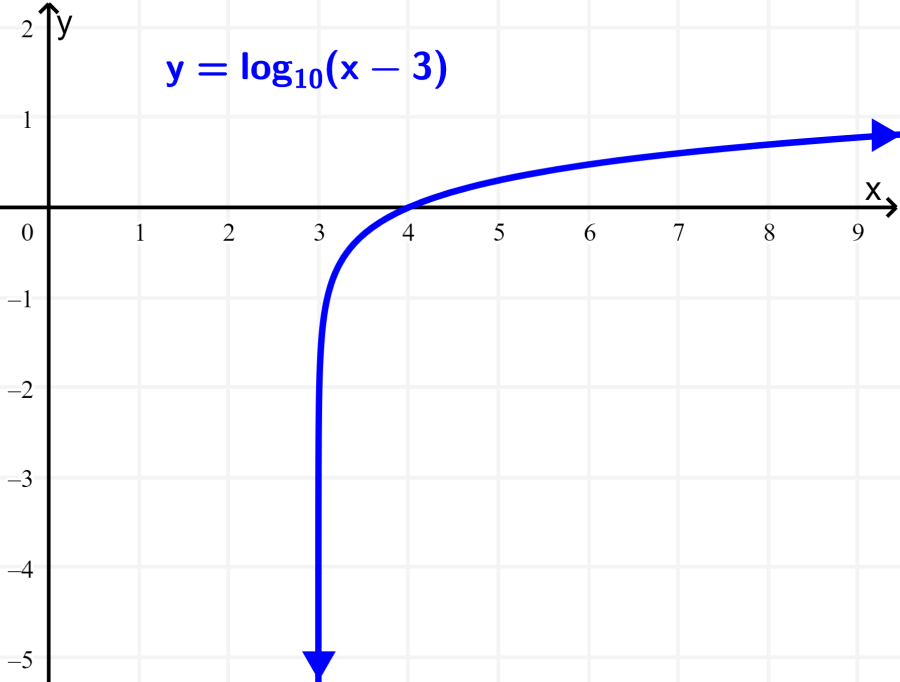
Find the domain and range of $latex f(x)=\log(x-3)$.
Solution: The value of h of 3 causes the “standard” function and its asymptote to move to the right by 3 units. This changes the domain of the function. Therefore, the domain is:
Domain: $latex 3<x<\infty$
The range of the function never changes so it remains:
Range: $latex -\infty<x<\infty$
EXAMPLE 3
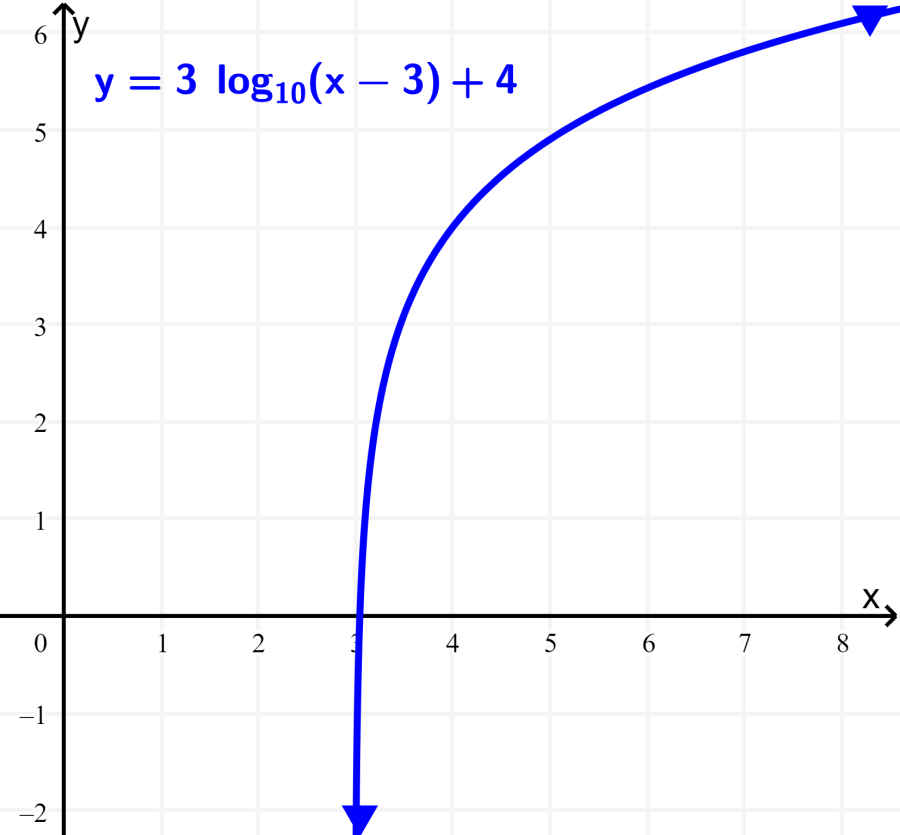
Find the domain and range of the function $latex f(x)=3\log(x-3)+4$.
Solution: The 3 represents a stretch of the graph and the 4 represents a vertical translation of the graph. These two values do not affect either the domain or the range of the logarithmic function, so both the domain and the range remain the same as in the previous example:
Domain: $latex 3<x<\infty$
Range: $latex -\infty<x<\infty$
EXAMPLE 4
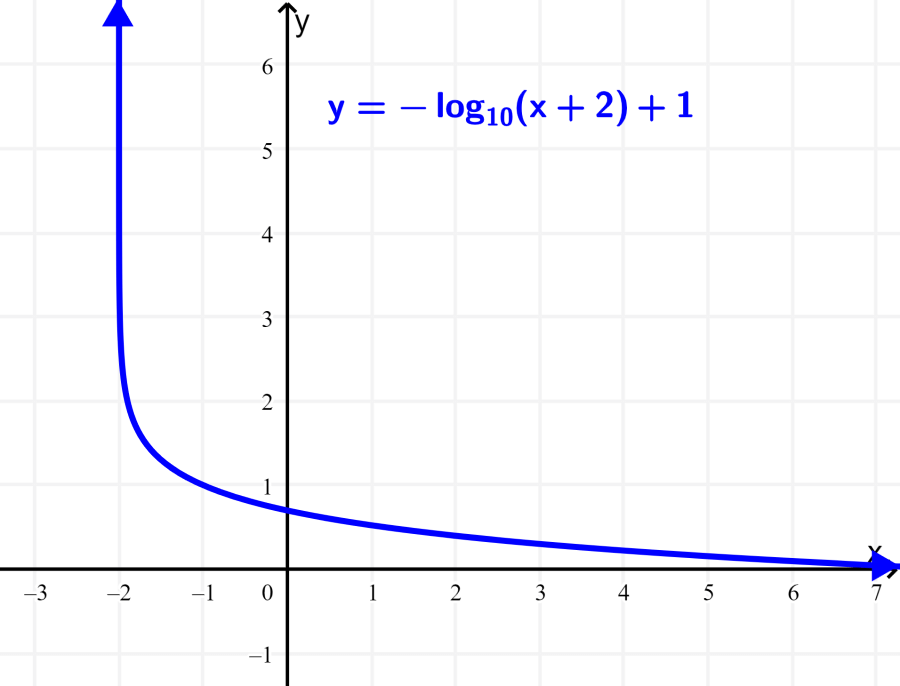
What is the domain and range of the function $latex f(x)=-\log(x+2)+1$?
Solution: This function has a graph that is reflected with respect to the x-axis. However, this does not change either domain or range. The only value that affects the domain is -2, which produces a 2-unit translation to the left of both the function and its asymptote. Therefore, the domain is:
Domain: $latex -2<x<\infty$
See also
Interested in learning more about the domain and range of functions? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
