The domain is the set of possible values for the inputs of the function, that is, the values of x. The range is the set of possible values for the outputs of the function, that is, the values of y. In this article, we will look at the definitions of domain and range in more detail. Then, we will explore some examples with answers of the domain and range of functions.
Definition of domain
The domain of the function is the set of all possible values of the independent variable. That is, the domain is the set of all the values of x that will work and will make the function return real values of y.
How to find the domain?
We can determine the domain of the function by looking for the values of the independent variable (usually x), which we can use in the function. Usually, this involves avoiding values that produce a 0 in the denominator of fractions or avoiding having negative values within square roots.
Therefore, to find the domain, the important thing to remember is that:
- The denominator of a fraction cannot be zero.
- The number within a square root must be positive.
EXAMPLE
The following is the graph of $latex y=\sqrt{{x + 2}}$:
The domain of this function is $latex x\ge -2$ because x cannot be less than -2. To verify this, we can try the number -3. Replacing $latex x=-3$, we have $latex y=\sqrt{{- 3+2}} = \sqrt{{- 1}}$.
We have a negative number within a square root and the result is not a real number. This means that only values of x greater than or equal to -2 produce real values in the function.
Definition of range
The range of the function is the set of all possible values of the dependent variable after substituting the domain. That is, the range is the resulting values of y that we obtain after having substituted all the possible values of x.
How to find the range?
To find the range we take into account the following:
- The range of a function is the set of values of y, from the minimum value to the maximum value.
- By plugging in some values of x, we can determine what happens to the values of y. We can find out if the y values are always positive, always negative, etc.
- Make sure to find the minimum and maximum values of y.
- Draw a basic graph to visualize the problem.
EXAMPLE
Again, let’s look at the graph of $latex y=\sqrt{{x+2}}$:
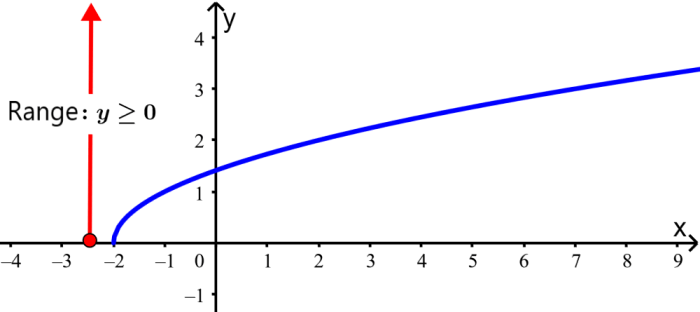
We can see that the curve is always above the horizontal axis. No matter what value of x we try, we will always get a value of y that is zero or positive. In this case, the range is $latex y \ge 0$.
The graph goes to the right indefinitely, so the range is all non-negative values of y.
How to find the domain and range without using a graph?
It’s always easier to determine the domain and the range of a function when we have a graph, as long as we make sure to zoom in and out to capture all the necessary details. However, graphing a function is not always possible as we may not have software or calculators to graph at any given time.
To find the domain and range without using a graph, we use what we saw earlier:
- We cannot have negative values within a square root sign.
- We cannot have zeros in the denominator of a fraction.
EXAMPLE
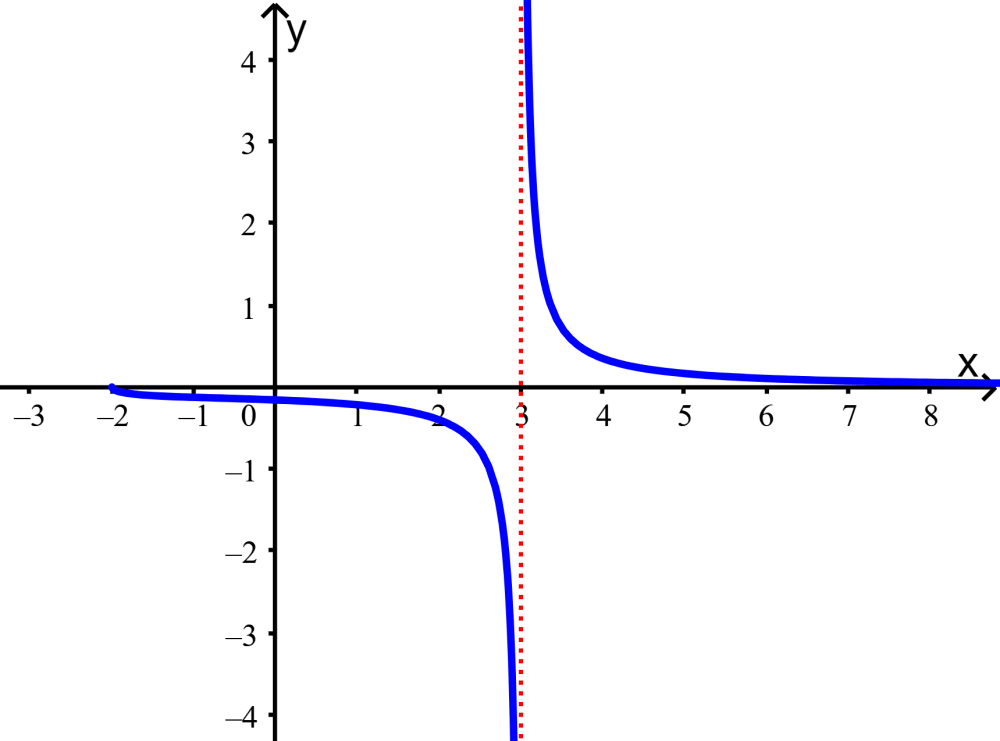
Find the domain and range of the function $latex f (x)=\frac{\sqrt{x+2}}{{{x}^2}-9}$ without using a graph.
Solution: In the numerator of the fraction, we have a square root. To ensure that the value under the root is non-negative, we can only use values of x that are greater than or equal to -2.
The denominator of the fraction has the expression $latex {{x}^2}-9$, which can be written as $latex (x + 3)(x-3)$. Therefore, our values for x cannot include -3 for the first parenthesis and 3 for the second parenthesis.
Thus, the domain for this function is $latex x \ge -2, ~~ x\ne 3$.
To determine the range, we consider the numerator and denominator of the function separately:
Numerator: If $latex x=-2$, we have $latex f (x)=\sqrt{{- 2 + 2}}=0$. As x increases, the numerator will also increase to infinity.
Denominator: We divide into the following parts:
When $latex x=-2$, the lower part of the function equals $latex {{(-2)}^2}-9=4-9=-5$. Then, we have $latex f(-2)=\frac{0}{- 5} = 0$.
Between $latex x=-2$ and $latex x= 3$, the expression $latex {{(x)}^2} – 9$ approaches 0, so the function will tend to infinity as we approach $latex x=3$.
For $latex x>3$, when x is slightly larger than 3, the denominator value is slightly larger than 0, so the function will have a very large positive value.
For very large values of x, the numerator will be large, but the denominator will be much larger, so the value of the function will get smaller and smaller.
Therefore, the range of the function is $latex (-\infty, ~ 0\big], ~ (\infty, ~ 0)$.
We can visualize this in the graph:
Domain and range – Examples with answers
EXAMPLE 1
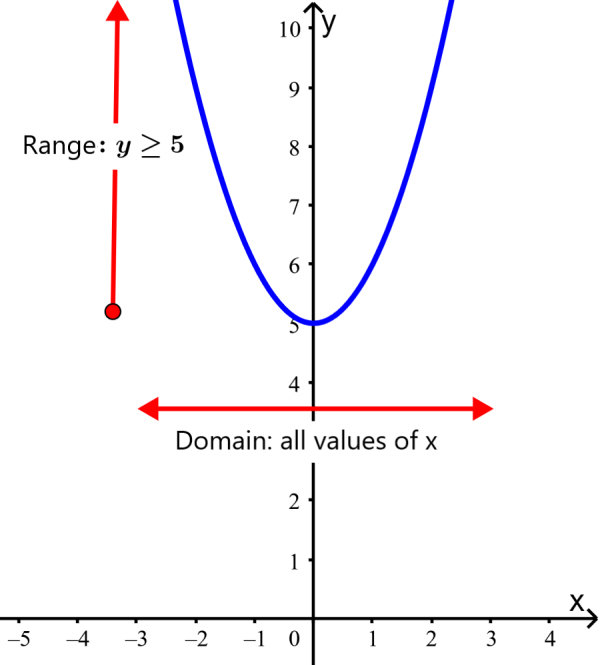
Find the domain and range for the function $latex f(x)={{x}^2}+5$.
Domain: The function $latex f(x)={{x}^2}+5$ is defined for all values of x since there is no restriction on the value of x. Therefore, the domain of $latex f(x)$ is “all real values of x“.
Range: Since $latex {{x}^2}$ is never negative, the function $latex f(x)={{x}^2}+5$ is never less than 5. Therefore, the range of $latex f(x)$ is “all real numbers $latex f(x) \ge 5$.
In the graph, we can see that the domain is all real numbers, but the range is all real numbers greater than 5:
EXAMPLE 2
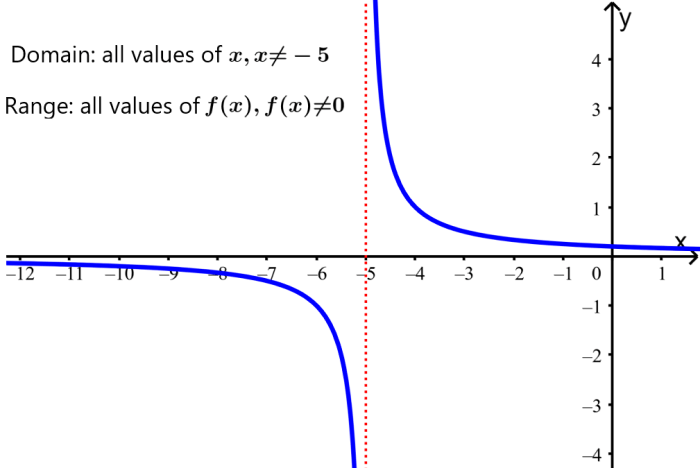
Find the domain and range for the function $latex f(x)=\frac{1}{x+5}$.
Domain: The function $latex f(x)=\frac{1}{x+5}$ is not defined for $latex x=-5$ since this value would produce a division by 0. Therefore, the domain of the function is all real numbers with the exception of -5.
Range: No matter how big or how small the values of x are, the function $latex f(x)$ will never equal 0. This means that the range of the function is all real numbers except 0.
In the graph we can see that the function is not defined for $latex x=-5$ and that the range is all integers except 0:
EXAMPLE 3
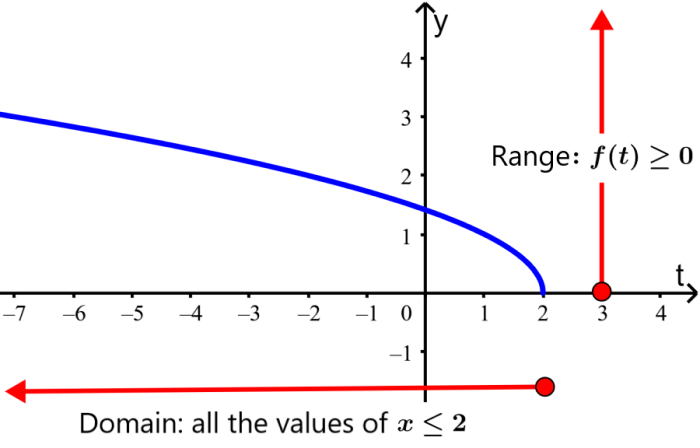
Find the domain and range for the function $latex f(t)=\sqrt{{2-t}}$.
Domain: The function $latex f(t)=\sqrt{{2-t}}$ is not defined for values greater than 2 since it would cause us to have a negative value within the square root. Then, the domain of the function is all real numbers less than or equal to 2, $latex t\le 2$.
Range: By definition we have $latex f(t)=\sqrt{{2-t}} \ge 0$.
In the graph we can see that t does not take values greater than 2 and the range is greater than or equal to 0:
See also
Interested in learning more about functions? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
