To determine when it is a function and when it is not, we have to look at the inputs and outputs of the relation. If the inputs of the relation produce only one output, then the relation is a function. Otherwise, if the inputs produce two or more outputs, the relation is not a function.
In this article, we will look at some examples with answers to the method used to determine if a relation is a function or not a function.
Definition of relations and functions
Relations
A relation is a set of inputs and outputs, often written as ordered pairs (inputs, outputs). The set of the first component of each ordered pair is called the domain and the set of the second component of each ordered pair is called the range.
For example, in the following set of ordered pairs, the first number in each pair are the first four natural numbers and the second numbers are the triple of the first:
{(1, 3), (2, 6), (3, 9), (4, 12)}
The domain is {1, 2, 3, 4} and the range is {3, 6, 9, 12}.
Each value in the domain is also known as an input or as an independent variable and is often represented by the letter x. Each value in the range is also known as an output or a dependent variable and is often represented by the letter y.
Functions
A function is a relationship that assigns a single value in the range to each value in the domain. This means that the values of x are not repeated. In the example we have above, we relate the first four natural numbers to triple these numbers.
This relationship is indeed a function since each element in the domain, {1, 2, 3, 4}, is paired with exactly one element in the range {3, 6, 9, 12}.
Now let’s look at another example. Consider the following ordered pairs, where we relate letters to numbers:
{(A, 1), (B, 2), (A, 3), (B, 4)}
Notice that each element in the domain {A, B}, is not paired with exactly one element in the range {1, 2, 3, 4}. For example, the letter A corresponds to two values in the range {1, 3} and the letter B corresponds to two values in the range {2, 4}. This means that this relationship is not a function.
In the following image we can compare relations that are functions and not functions:
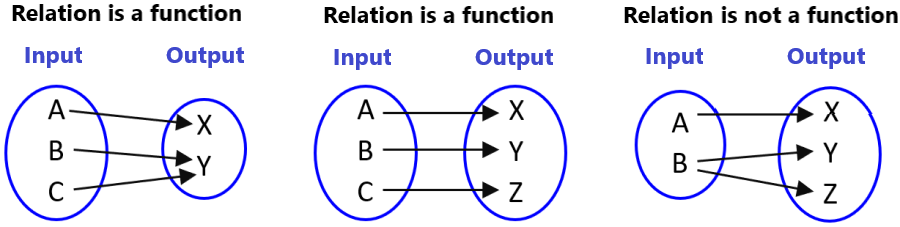
How to determine when it is a function and when it is not?
To determine if it is a function or not, we can use the following:
1. Identify the input values.
2. Identify the output values.
3. If each input value produces only one output value, the relation is a function. If each input value produces two or more output values, the relation is not a function.
We can also solve graphically by using the line test in mapping diagrams or the vertical line test for graphs.
Line test in mapping diagrams
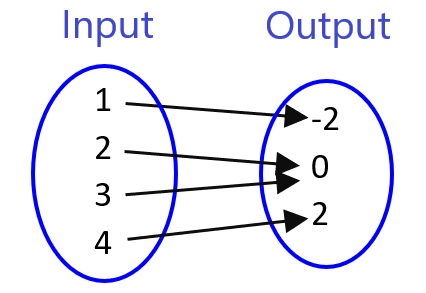
To verify if a relationship is a function using mapping diagrams, we use the following criteria: if each input has only one connected line, then the outputs do represent a function.
For example, in the following mapping diagram, y is a function of x, but x is not a function of y.
Vertical line test for graphs
To determine if y is a function of x given a graph of the relation, we can use the following criteria: if all vertical lines that can be drawn pass through a single point on the graph, then the relation is a function. If it is possible to draw a vertical line that passes through at least two points on the graph, then the relation is not a function.
For example, in the following graph, we can see that y is a function of x:
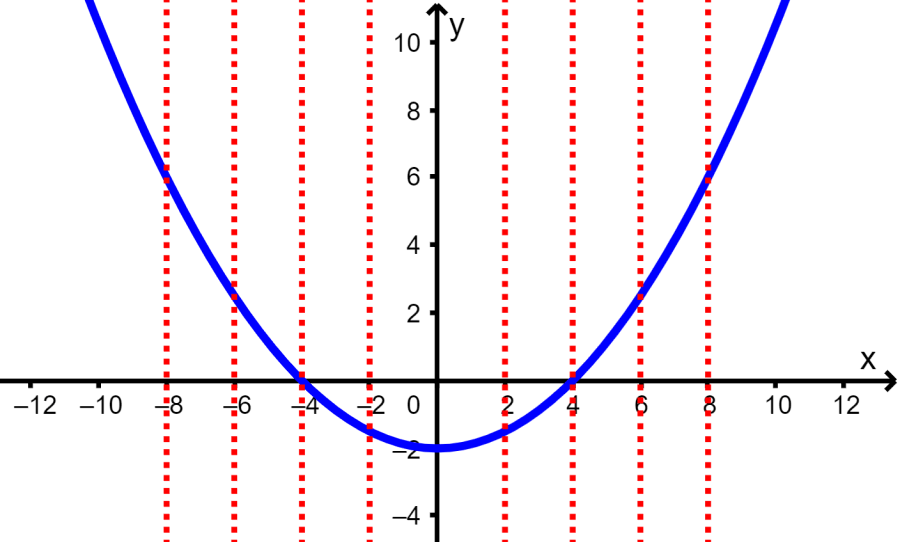
Function or not a function – Examples
EXAMPLE 1
Determine whether the price lists for a menu are functions.
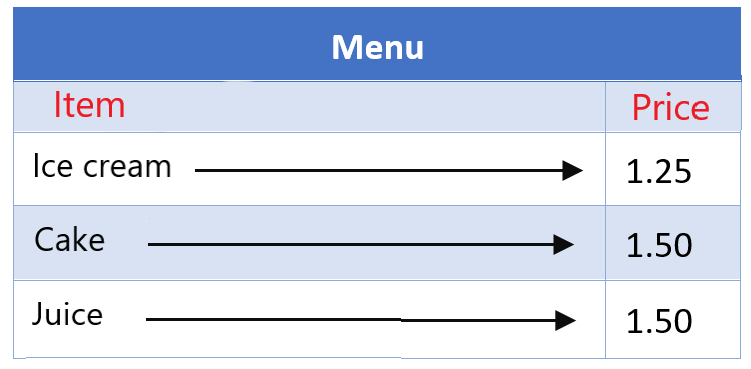
We have the menu shown in the following image, which consists of items and their prices.
1. Is the price a function of the item?
2. Is the item a function of the price?
Solution:
1. We are going to consider the elements as the inputs. Therefore, the prices are the starting values. Each item on the menu has only one price, which means that the price is a function of the item.
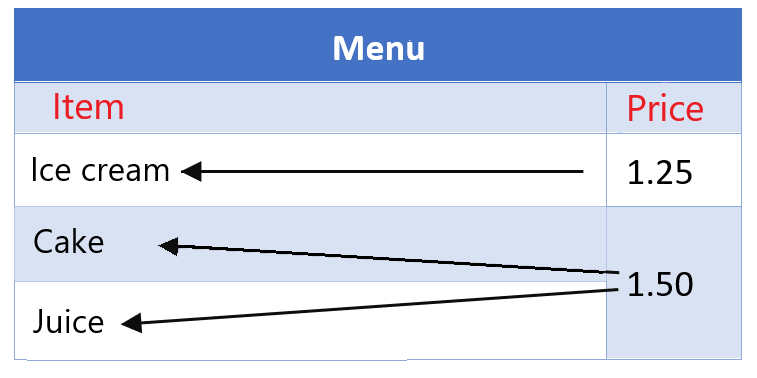
2. Now let’s consider prices as the inputs. We see that two menu items have the same price. This means that the inputs have more than one output value assigned, therefore it does not represent a function. Items are not a function of price.
EXAMPLE 2
Determine if the following mapping diagram represents a function.
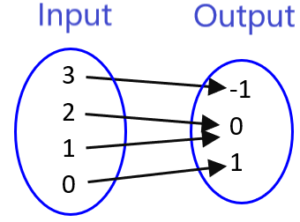
Solution: We can easily see that each input value corresponds to a single output value, so the mapping diagram does represent a function.
EXAMPLE 3
Determine whether the following graph represents a function.
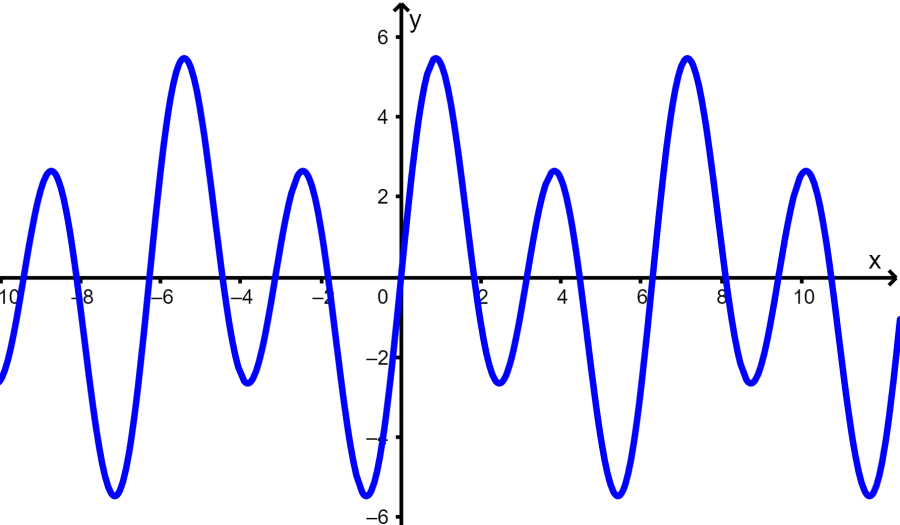
Solution: We can use the vertical line test to determine whether it is a function or not:
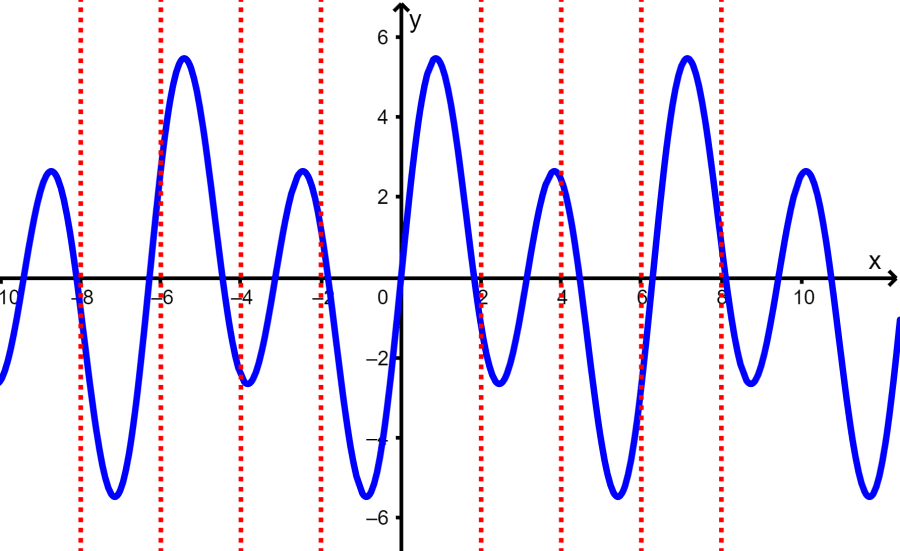
We see that the vertical lines are drawn across the function at a single point, so the graph does represent a function.
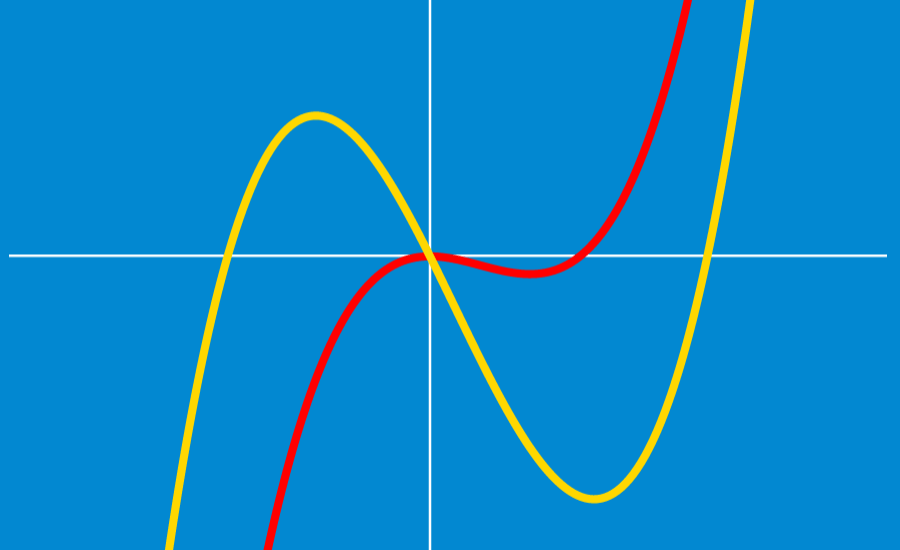
EXAMPLE 4
Determine whether the following graph represents a function.
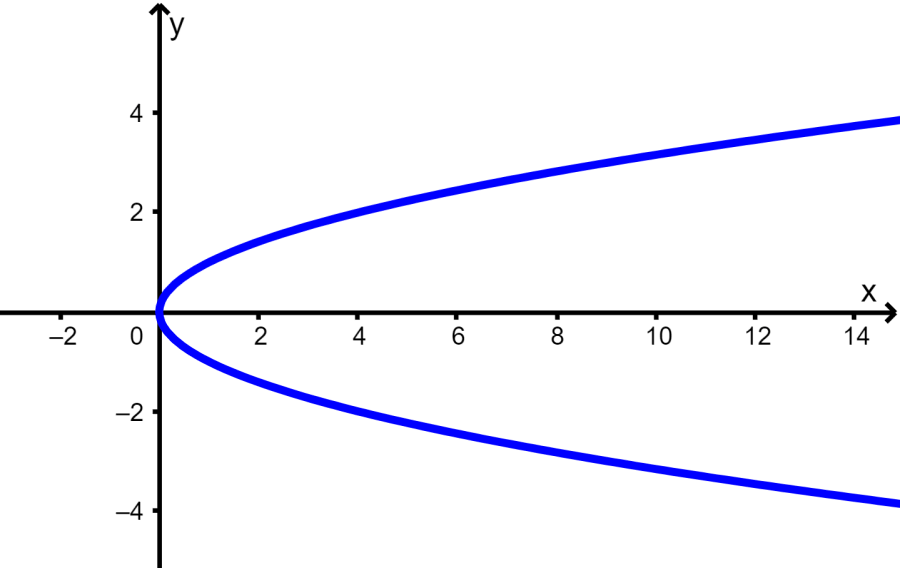
Solution: Again, we use the vertical line test to determine whether the graph is a function or not:
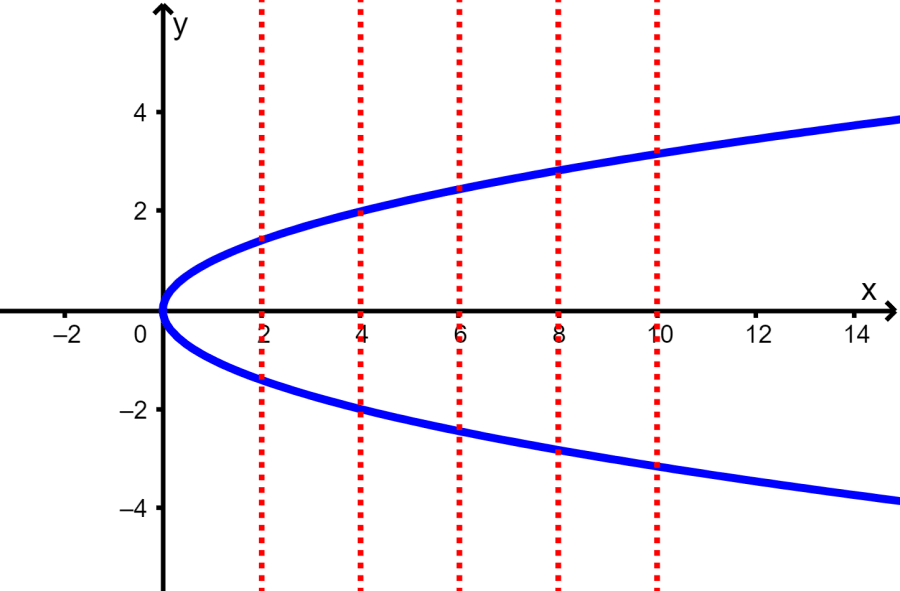
By drawing several vertical lines, we see that it is possible for a vertical line to cross the graph at more than one point. This means that the graph does not represent a function.
See also
Interested in learning more about functions? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
