Applications of Quadratic Functions

Important applications of quadratic functions

There are several important applications of quadratic functions in mathematics and other fields, including:

Physics

Quadratic functions can be applied in physics to model the motion of particles and rigid bodies under the influence of forces.

For example, the equations of motion of a projectile under the influence of gravity can be modeled using a quadratic function.

Engineering

Quadratic functions are used to design and analyze structures and mechanical systems, such as bridges and buildings. For example, the deflection of a beam under a load can be modeled using a quadratic function.

Economy

We can use quadratic functions to model the relationship between supply and demand and to analyze market equilibrium. That is, it allows us to understand the relationship between price and quantity supplied and demanded in a market.

Optimization

Quadratic functions are used in optimization problems, such as finding the minimum or maximum value of a function.

For example, in machine learning, quadratic functions are used in linear and quadratic programming to find the best parameters for a model that minimizes an error function.

Geometry

Quadratic functions are used to define and analyze parabolas, which are the set of all points that are equidistant from a fixed point and a fixed line.

Signals processing

Audio and image signals can be modeled and processed using quadratic functions. For example, in audio signal processing, quadratic functions are used to model the frequency response of audio filters and equalizers.

Quantum mechanics

In quantum mechanics, quadratic functions are used to describe the behavior of the wave properties of subatomic particles.

---

Finding areas

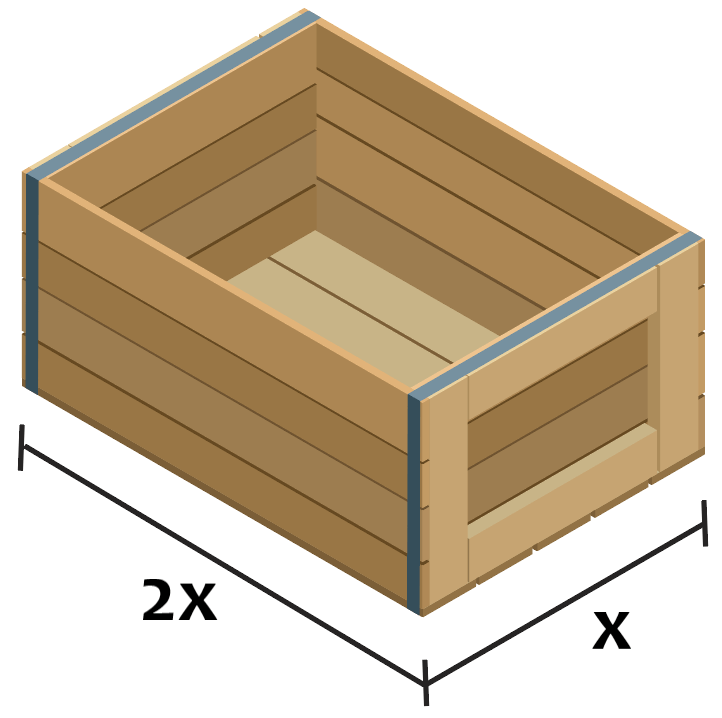
In our day to day, many times we have to find the area of an apartment, the area of a lot of land, or the area of boxes and other objects. An example of this involves building a rectangular box where one side must be twice the length of the other side.

For instance, if we only have 9 square meters to use for the bottom of the box, with this information, we can create an equation for the area of the box using the proportions between both sides.

This means that the area, which is equal to the length times the width, in terms of x would be equal to x times 2x or $latex 2{{x}^2}$. This equation must be equal to or less than 9 in order to construct a box under these constraints.

---

Finding profit

Quadratic functions can often be used to calculate the profits of a business. If we want to sell something, even if it is something simple like cookies, we need to determine how many packages to produce so that we can make a profit.

For example, if we are selling packages of cookies and we want to produce 20 packages, we know that we will sell a different number of packages depending on how we set the price.

If we price 100 dollars per package, we may not sell any packages, but if we price 0.01 dollars per package, we will probably sell all 20 packages in a minute.

Therefore, to decide the price to use, we can make P a variable. We estimate the demand for the cookie packages to be 20-P. Then, the revenue will be equal to the price multiplied by the number of packages sold: $latex P(20-P)=20P -{{P}^2}$. Using the cost of producing the cookie packages, we can make our equation equal to that quantity and from there choose a price.

---

Quadratic functions in sports

Quadratic functions are very useful in sporting events that involve throwing objects such as the javelin or discus throw. For example, let’s say you throw a ball into the air and want your friend to catch it, but you want to give him the precise time the ball will arrive.

We can use the equation of velocity, which calculates the height of the ball based on a parabolic or quadratic equation. Then, suppose we throw the ball from a height of 2 meters.

Let’s also assume that we are throwing the ball upward at a speed of 10 meters per second and that the Earth’s gravity is slowing the ball down at a rate of 5 meters per second squared.

With these data, we can calculate the height of the ball, h, using the variable t for time in the equation $latex h=2+10t-5{{t}^2}$. If your friend’s arms are also 2 meters high, how many seconds will it take for the ball to reach him? To answer this we use $latex h = 2$ and solve for t. The answer is approximately 2 seconds.

---

Calculating speeds

Quadratic equations and functions are also useful for calculating speeds. For example, more experienced kayakers use quadratic equations to estimate their speed when moving along a river. Let’s assume that a kayaker is traveling upstream and the river is moving at 3 kilometers per hour.

If you travel upstream against the current for 10 km and the round trip takes 2 hours, we remember that $latex \text{time}=\frac{\text{distance}} {\text{speed}}$, where we use $latex v=\text{kayak speed relative to land}$ and we use $latex x=\text{kayak speed through water}$.

As the kayaker travels upstream, the kayak’s speed is $latex v=x-3$. We subtract 3 due to the resistance of the river current, and as he travels downstream, the kayak’s speed is $latex v=x + 3$.

The total time is equal to 2 hours, which is equal to the time spent traveling upstream plus the time spent traveling downstream, and both distances are 10 km. Using our equations, we know that $latex 2\text{hours} = \frac{10}{x-3}+\frac{10}{x + 3}$.

Once we expand this algebraically, we get $latex 2{{x}^2}-20x-18 = 0$. By solving for x, we know that the kayaker moved his kayak at a speed of 10.83 kilometers per hour.

---

See also

Interested in learning more about applications of functions? Take a look at these pages:

• Applications of Linear Functions
• Applications of Trigonometric Functions
• Applications of Exponential Functions
• Applications of Rational Functions
• Applications of Logarithmic Functions
• Applications of Complex Numbers