The triangular inequality is one of the most commonly known theorems in geometry. This theorem tells us that the sum of two of the sides of the triangle is greater than the third side of the triangle. If we have a segment that is greater than the sum of the other two segments, we cannot form a triangle.
Here, we will learn more details about the triangular inequality along with some examples.
What is the triangle inequality?
The triangle inequality is a theorem that states that in any triangle, the sum of two of the three sides of the triangle must be greater than the third side. For example, in the following diagram, we have the triangle ABC:
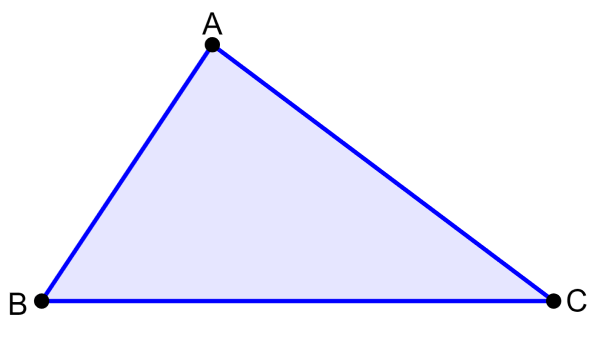
The triangle inequality tells us that:
- The sum AB+BC must be greater than AC. Therefore, we have AB+BC>AC.
- The sum AB+AC must be greater than BC. Therefore, we have AB+AC>BC.
- The sum BC+AC must be greater than AB. Therefore, we have BC+AC>AB.
We can understand the triangle inequality by imagining that we are walking along the sides of triangle ABC. If we have to go from point A to point B, the shortest path is the straight line AB. If we go to C first and then to B, the distance we traveled, AC+CB, will definitely be greater than AB.
If the sum of the two sides was not greater than the third side, we could not form a triangle since one of the segments would be too short to connect the other two.
Proof of the triangle inequality
We can obtain a proof of the triangular inequality considering the following triangle ABC:
We are going to prove that AB+AC>BC. Then, we extend segment BA to point D, in such a way that we have segments AD=AC. Then, we connect points C and D as shown in the diagram:
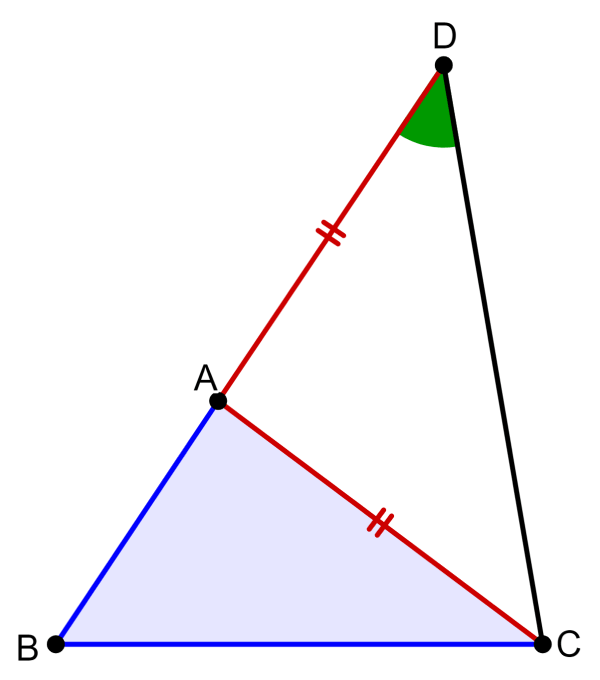
We can see that the angles ∠ACD and ∠D are equal. This means that in triangle BCD, we have ∠BCD>∠D. Also, we know that sides that are opposite to large angles are also large, so we have BD> BC.
Segment BD equals AB+AD. Therefore, we have AB+AD>BC. Finally, we know that AD=AC, so we have:
AB + AC>BC
Triangle inequality with vectors
In the following diagram, we have a triangle formed by the vectors $latex \vec{a}$, $latex \vec{b}$ and $latex \vec{a}+\vec{b}$.
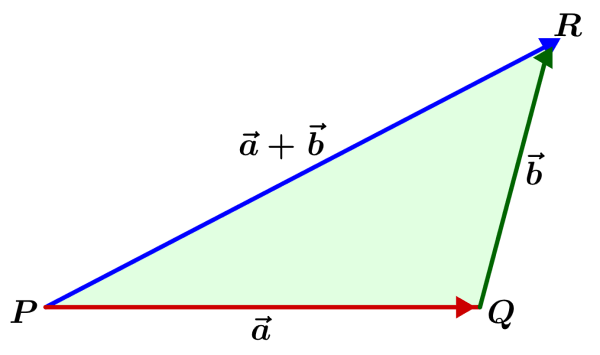
We know that in a triangle, the sum of two sides is always greater than the third side. In the triangle above, we have $latex PQ=|\vec{a}|$, $latex QR=|\vec{b}|$ and $latex PR=|\vec{a}+\vec{b}|$. Therefore, we have:
$latex |\vec{a}+\vec{b}|<|\vec{a}|+\vec{b}|$
Furthermore, we also know that the difference between the two sides is less than the third side. Therefore, we have:
$latex |\vec{a}|-|\vec{b}|<|\vec{a}+\vec{b}|$
When we combine these two inequalities, we have:
$latex |\vec{a}|-|\vec{b}|<|\vec{a}+\vec{b}|<|\vec{a}|+\vec{b}|$
Solved problems of triangular inequality
EXAMPLE 1
Determine whether it is possible to form a triangle with three segments that have lengths of 8 units, 6 units, and 5 units.
Solution: We can start by assigning the values a=8, b=6 and c=5. Therefore, we have:
a+b>c
⇒ 8+6>5
⇒ 14>5 (true)
a+c>b
⇒ 8+5>6
⇒ 13>6 (true)
b+c>a
⇒ 6+5>8
⇒ 11>8 (true)
Since all the conditions are true, it is possible to form a triangle with the given measurements.
EXAMPLE 2
Is it possible to form a triangle with the segments that have lengths of 12 units, 6 units, and 5 units?
Solution: Again, we assign the values a=12, b=6 and c=5. Therefore, we have:
a+b>c
⇒ 12+6>5
⇒ 18>5 (true)
a+c>b
⇒ 12+5>6
⇒ 17>6 (true)
b+c>a
⇒ 6+5>12
⇒ 11>12 (not true)
One of the conditions is not true, so we cannot form a triangle with these measurements.
See also
Interested in learning more about similar figures, congruency and other geometry topics? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
