Revolutions are a way of measuring complete turns in circles. Revolutions are used in various situations where an object makes a large number of turns and it is more convenient to measure the number of turns the object makes per minute or per second. For example, revolutions per minute (RPM) are used to measure the rotation of engines, tires, or other objects. One revolution is equivalent to 2π radians. Therefore, to convert from radians to revolutions, we divide the radians by 2π.
Here, we will use the radians to revolutions transformation formula to solve some practice problems.
TRIGONOMETRY
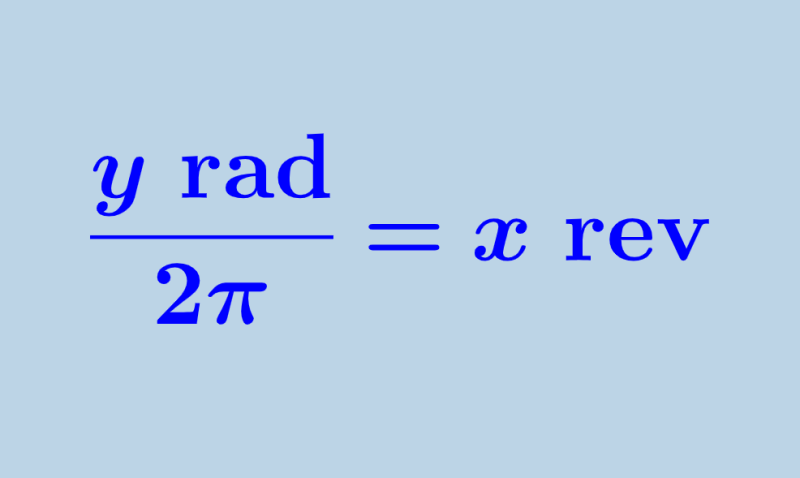
Relevant for…
Learning to transform from radians to revolutions with examples.
TRIGONOMETRY
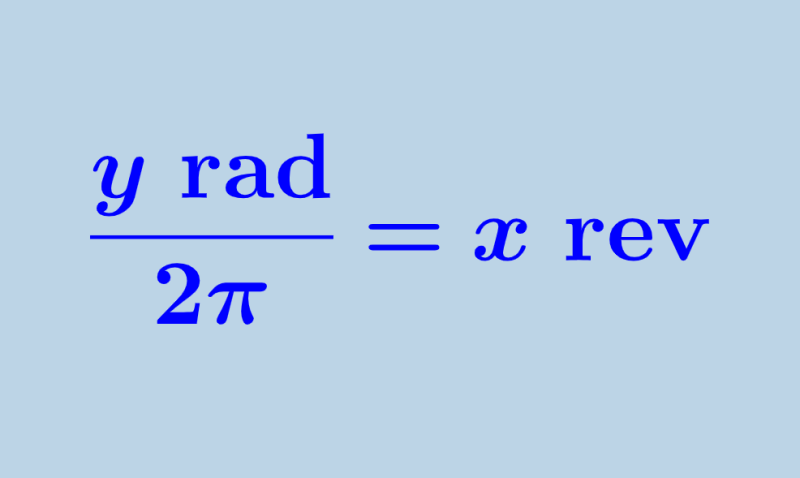
Relevant for…
Learning to transform from radians to revolutions with examples.
How to convert from radians to revolutions?
We can convert from radians to revolutions by dividing the number of radians by 2π and we will get the number of turns that is equal to the given radians. This means that we have the following formula:
| $latex \frac{y\text{ rad}}{2\pi}=x \text{ rev}$ |
where y represents the given radians and x is the response in revolutions.
Radians in a circle
The formula for the transformation from radians to revolutions is derived by considering that we have 2π radians when we make a complete revolution of a circle. Radians are related to the radius of a circle as we can see in the following animation.
Also, we know that one revolution equals one complete turn. Therefore, we have the relationship 1 rev = 2π rad. Therefore, to get the number of revolutions in a given number of radians, we simply divide the number of radians by 2π.
Transformation from radians to revolutions – Examples with answers
Each of the following examples is solved using the transformation formula from radians to revolutions seen above. Try to solve the problems yourself before looking at the answer.
EXAMPLE 1
How many revolutions are equal to 4π radians?
Solution
Using the formula given above with the given value, we have:
$latex \frac{y \text{ rad}}{2\pi}=x \text{ rev}$
$latex \frac{4\pi \text{ rad}}{2\pi}=2 \text{ rev}$
Therefore, 4π radians is equal to 2 revolutions.
EXAMPLE 2
If we have 12π radians, what is its equivalent in revolutions?
Solution
We substitute the given value in the transformation formula to obtain:
$latex \frac{y \text{ rad}}{2\pi}=x \text{ rev}$
$latex \frac{12\pi \text{ rad}}{2\pi}=6 \text{ rev}$
Therefore,12π radians is equivalent to 6 revolutions.
EXAMPLE 3
How many revolutions are equal to 7π radians?
Solution
We have $latex y=7\pi$. Using this value in the formula given above, we have:
$latex \frac{y \text{ rad}}{2\pi}=x \text{ rev}$
$latex \frac{7\pi \text{ rad}}{2\pi}=3.5 \text{ rev}$
Therefore, 7π radians is equal to 3.5 revolutions.
EXAMPLE 4
If we have 12 radians, how many revolutions do we have?
Solution
In this case, we have $latex y = 12$. By substituting this value in the formula, we get:
$latex \frac{y \text{ rad}}{2\pi}=x \text{ rev}$
$latex \frac{12 \text{ rad}}{2\pi}=1.91 \text{ rev}$
Therefore, 12 radians is equivalent to 1.91 revolutions.
EXAMPLE 5
How many revolutions are equivalent to 24 radians?
Solution
We substitute the value $latex y = 24$ in the formula to obtain:
$latex \frac{y \text{ rad}}{2\pi}=x \text{ rev}$
$latex \frac{24 \text{ rad}}{2\pi}=3.82 \text{ rev}$
Therefore, 24 radians is equal to 3.82 revolutions.
Radians to revolutions – Practice problems
Solve the following practice problems using the radians to revolutions transformation formula. Select an answer and check it to see if you got the correct answer.
See also
Interested in learning more about radians and degrees? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
