Degrees and radians are the two most common types of units for measuring angles. Each of these units is suitable in different situations. Degrees are used in geometry as they allow us to measure an angle and indicate a direction. However, technically speaking, angles are not numbers and we can only perform mathematical calculations with numbers. For this reason, radians are more convenient when working on calculus or other advanced mathematical topics. To convert from degrees to radians, we have to multiply by π and divide by 180°.
Here, we will learn about the process used to convert from degrees to radians with practice problems.
TRIGONOMETRY
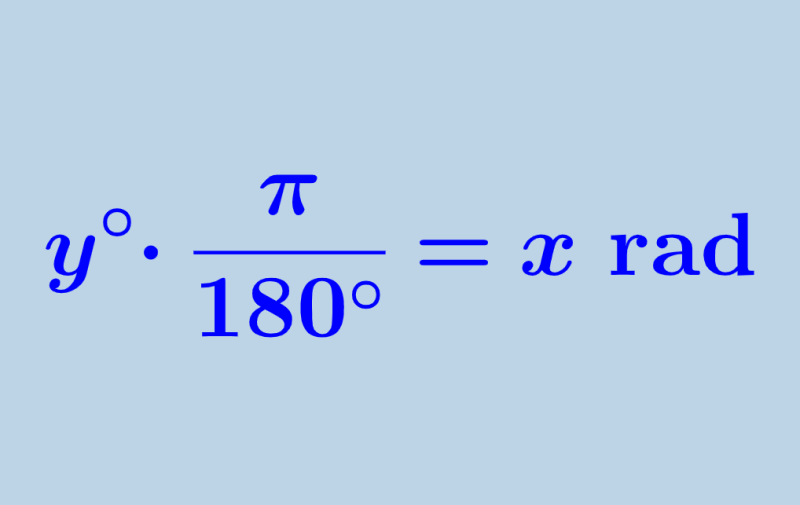
Relevant for…
Learning to transform from degrees to radians with examples.
TRIGONOMETRY
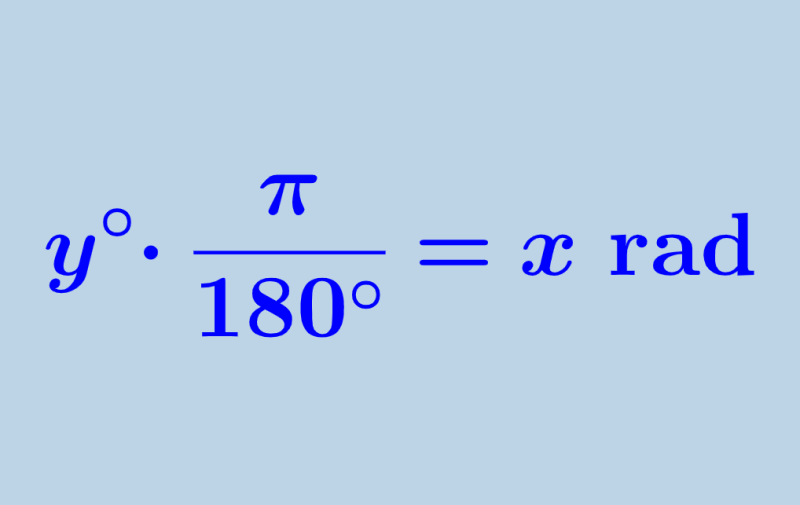
Relevant for…
Learning to transform from degrees to radians with examples.
How to convert from degrees to radians?
We can convert from degrees to radians by multiplying the given angle by π and dividing by 180°. This means that we have the following formula:
| $latex y^{\circ}\cdot \frac{\pi}{180^{\circ}}=x$ rad |
Here, y represents the angle in degrees and x is the answer in radians.
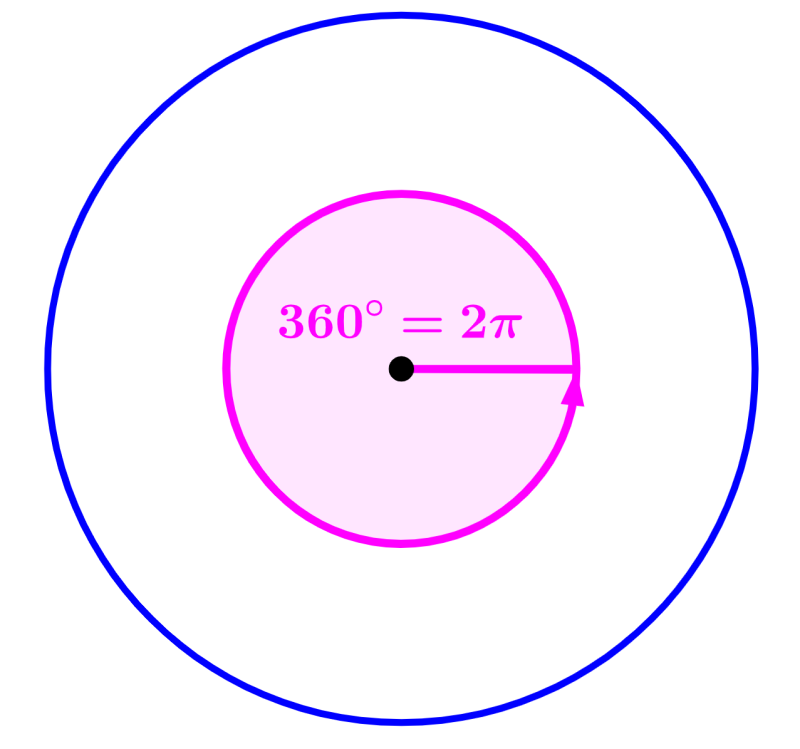
We can derive this formula by considering that we have 360° in a complete circle. Furthermore, we also know that one complete turn is equivalent to 2π radians. Therefore, we can form the relationship 2π = 360°.
Now, we can simplify this relationship by dividing both sides by two. Dividing by two, we get π = 180°. This is the relationship used to convert from degrees to radians.
Transformation from degrees to radians – Examples with answers
The formula for the transformation from degrees to radians is used to solve the following examples. Try to solve the problems yourself before looking at the answer.
EXAMPLE 1
How many radians is equal to 240°?
Solution
We use the transformation formula with the given value. Therefore, we have:
$latex y^{\circ}\cdot \frac{\pi}{180^{\circ}}=x$ rad
$latex 240^{\circ}\cdot \frac{\pi}{180^{\circ}}= \frac{4\pi}{3}$ rad
Thus, 240° is equivalent to $latex \frac{4\pi}{3}$ radians.
EXAMPLE 2
Convert 200° to radians.
Solution
We use the angle given in the formula seen above to obtain:
$latex y^{\circ}\cdot \frac{\pi}{180^{\circ}}=x$ rad
$latex 200^{\circ}\cdot \frac{\pi}{180^{\circ}}= \frac{10\pi}{9}$ rad
Therefore, 200° is equal to $latex \frac{10\pi}{9}$ radians.
EXAMPLE 3
How many radians is equal to 86°?
Solution
We substitute the given angle in the transformation formula to obtain:
$latex y^{\circ}\cdot \frac{\pi}{180^{\circ}}=x$ rad
$latex 86^{\circ}\cdot \frac{\pi}{180^{\circ}}= \frac{43\pi}{90}$ rad
Then, the angle 86° is equivalent to$latex \frac{43\pi}{90}$ radians or 1.5 radians.
EXAMPLE 4
Convert 110° to radians.
Solution
We substitute the given value in the transformation formula and we have:
$latex y^{\circ}\cdot \frac{\pi}{180^{\circ}}=x$ rad
$latex 110^{\circ}\cdot \frac{\pi}{180^{\circ}}= \frac{11\pi}{18}$ rad
Therefore, 110° is equivalent to $latex \frac{11\pi}{18}$ radians or 1.92 radians.
EXAMPLE 5
What is 68° in radians?
Solution
We use the transformation formula with the given value. Therefore, we have:
$latex y^{\circ}\cdot \frac{\pi}{180^{\circ}}=x$ rad
$latex 68^{\circ}\cdot \frac{\pi}{180^{\circ}}= \frac{17\pi}{45}$ rad
Thus, 68° is equivalent to $latex \frac{17\pi}{45}$ radians or 1.19 radians.
Degrees to radians – Practice problems
Solve the following practice problems using the degrees to radians transformation formula. If you need help with this, you can look at the solved examples above.
See also
Interested in learning more about radians and degrees? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
