The law of cosines is the ratio of the lengths of the sides of a triangle with respect to the cosine of its angle. The law of cosines tells us that the square of one side is equal to the sum of the squares of the other sides minus twice the product of these sides and the cosine of the intermediate angle. This law is used when we want to find the length of a third side and we know the lengths of the two sides and the angle between them.
Here, we will learn about the formula for the law of cosines. We will learn to derive this formula and apply it to solve some practice problems.
Formula for the law of cosines
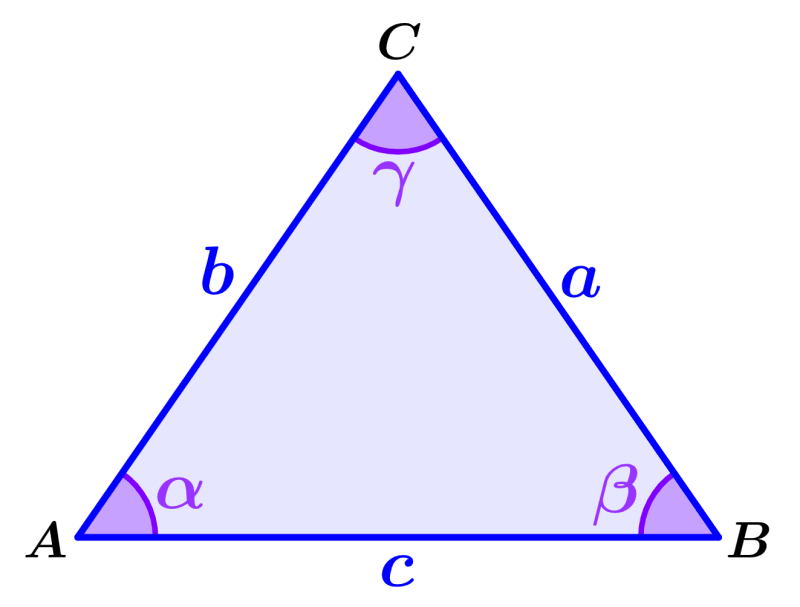
The law of cosines relates the lengths of two sides to their intermediate angle to find the length of a third side. The formulas for the law of cosines of a triangle ABC are given by:
| $latex {{a}^2}={{b}^2}+{{c}^2}-2bc\cos(\alpha)$ $latex {{b}^2}={{a}^2}+{{c}^2}-2ac\cos(\beta)$ $latex {{c}^2}={{a}^2}+{{b}^2}-2ab\cos(\gamma)$ |
Here, a, b, c are the lengths of the sides of the triangle, and α, β, γ are the angles of the triangle ABC shown in the diagram below.
When does the law of cosines apply?
By using basic trigonometric functions like sine, cosine, and tangent, we can find additional information about triangles. The law of cosines applies in the following situations:
- When we have the lengths of two sides and their intermediate angle and we want to find the length of the third side.
- When we have the lengths of the three sides of the triangle and we want to find the measure of any angle.
Therefore, an example of applying the law of cosines is finding the length of side c in the triangle below if we know the lengths of a and b and the measure of angle γ.
How to prove the law of cosines?
To prove the law of cosines, we are going to use the following triangle:
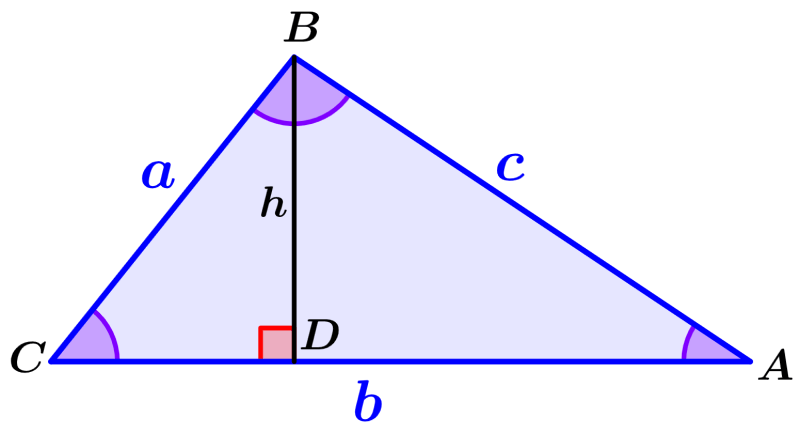
We can use the cosine function in triangle BCD. Recall that the cosine of an angle is equal to the adjacent side divided by the hypotenuse. Therefore, we have:
$latex \cos(C)=\frac{CD}{a}$
$latex CD=a~\cos(C)$
We can find the length of DA by subtracting CD from b :
$latex DA=b-CD$
$latex DA=b-a~\cos(C)$
Now, we use the sine function on triangle BCD. Recall that the sine of an angle is equal to the opposite side divided by the hypotenuse. Therefore, we have:
$latex \sin(C)=\frac{BD}{a}$
$latex BD=a~\sin(C)$
We apply the Pythagorean theorem on the triangle ADB:
$latex {{c}^2}={{BD}^2}+{{DA}^2}$
We use the expressions for BD and DA that we obtained earlier and substitute them in this equation:
$latex {{c}^2}={{(a~\sin(C))}^2}+{{(b-a~\cos(C))}^2}$
Expanding on the right side, we have:
$${{c}^2}={{a}^2}{{\sin}^2}(C)+{{b}^2}-2ab\cos(C)+{{a}^2}{{\cos}^2}(C)$$
Rearranging this equation and extracting the common factor $latex {{a}^2}$, we have:
$${{c}^2}={{a}^2}{{\sin}^2}(C)+{{a}^2}{{\cos}^2}(C)+{{b}^2}-2ab\cos(C)$$
$${{c}^2}={{a}^2}({{\sin}^2}(C)+{{\cos}^2}(C))+{{b}^2}-2ab\cos(C)$$
We can simplify to this equation using the identity $latex {{\sin}^2}(\theta)+{{\cos}^2}(\theta)=1$. Therefore, we have:
$latex {{c}^2}={{a}^2}+{{b}^2}-2ab\cos(C)$
With this, we have proved the law of cosines.
Law of cosines – Examples with answers
The following examples are solved by applying the formulas for the law of cosines. Each example has its respective solution, but it is recommended that you try to solve the problems yourself before looking at the answer.
EXAMPLE 1
What is the length of side c if we have lengths a=6 and b=7 and angle C=40°?
Solution
We begin by identifying the following information:
- a=6
- b=7
- C=40°
Using the law of cosines, we have:
$latex {{c}^2}={{a}^2}+{{b}^2}-2ab~\cos(C)$
$latex {{c}^2}={{6}^2}+{{7}^2}-2(6)(7)~\cos(40)$
$latex {{c}^2}=36+49-64.35$
$latex {{c}^2}=20.65$
$latex c=4.54$
The length of c is 4.54.
EXAMPLE 2
If we have the lengths b=10 and c=8 and the angle A=25°, what is the length of side a?
Solution
We can identify the following:
- b=10
- c=8
- A=25°
Using the law of cosines, we have:
$latex {{a}^2}={{b}^2}+{{c}^2}-2bc~\cos(A)$
$latex {{a}^2}={{10}^2}+{{8}^2}-2(10)(8)~\cos(25)$
$latex {{a}^2}=100+64-145$
$latex {{a}^2}=19$
$latex a=4.36$
The length of a is 4.36.
EXAMPLE 3
We have a triangle with sides of length a=5, b=7, and c=6. What is the measure of angle A?
Solution
We have the following:
- a=5
- b=7
- c=6
In this case, we have to use the law of cosines to find an angle. Therefore, we have:
$latex {{a}^2}={{b}^2}+{{c}^2}-2bc~\cos(A)$
$latex {{5}^2}={{7}^2}+{{6}^2}-2(7)(6)~\cos(A)$
$latex 25=49+36-2(7)(6)~\cos(A)$
$latex 25=85-84~\cos(A)$
$latex 84~\cos(A)=60$
$latex A={{\cos}^{-1}}(\frac{60}{84})$
$latex A=44.4$°
Angle A measures 44.4°.
EXAMPLE 4
In a triangle, we have the sides a=10, b=12, and c=8. What is the measure of angle C?
Solution
We can extract the following information:
- a=10
- b=12
- c=8
We use the law of cosines and solve for angle C:
$latex {{c}^2}={{a}^2}+{{b}^2}-2ab~\cos(C)$
$latex {{8}^2}={{10}^2}+{{12}^2}-2(10)(12)~\cos(C)$
$latex 64=100+144-2(10)(12)~\cos(C)$
$latex 64=244-240~\cos(C)$
$latex 240~\cos(C)=180$
$latex C={{\cos}^{-1}}(\frac{180}{240})$
$latex C=41.4$°
Angle C measures 41.4°.
Law of cosines – Practice problems
Use the formula for the law of cosines to solve the following practice problems. Select an answer and click “Verify” to check that you got the correct answer.
See also
Interested in learning more about the law of sines and cosines? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
