Hyperbolas are conic sections formed when a plane intersects a pair of cones. Hyperbolas have the characteristic that the difference of the distances from any point on the curve to the two foci is equal to a constant. Hyperbolas are made up of two branches that have a parabolic shape. All hyperbolas have two lines of symmetry, which intersect at the center.
Here, we will look at a more detailed definition of hyperbolas and we will learn about some of their most important characteristics.
PRECALCULUS
Relevant for…
Learning about the fundamental characteristics of hyperbolas.
PRECALCULUS
Relevant for…
Learning about the fundamental characteristics of hyperbolas.
Definition of a hyperbola
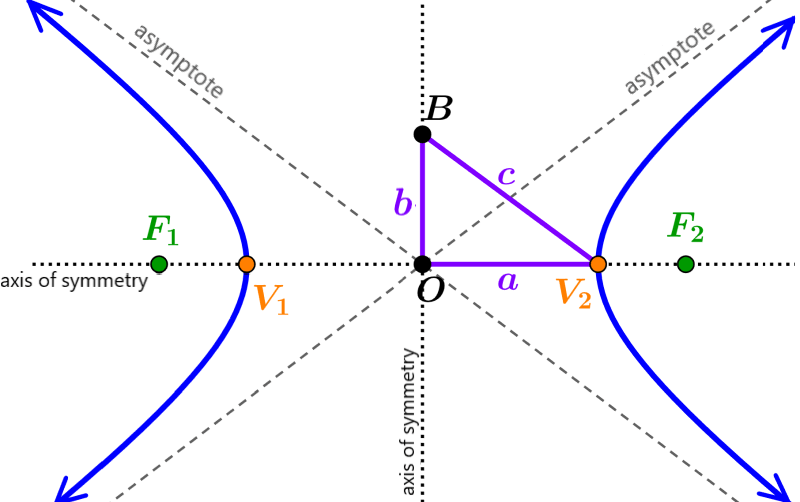
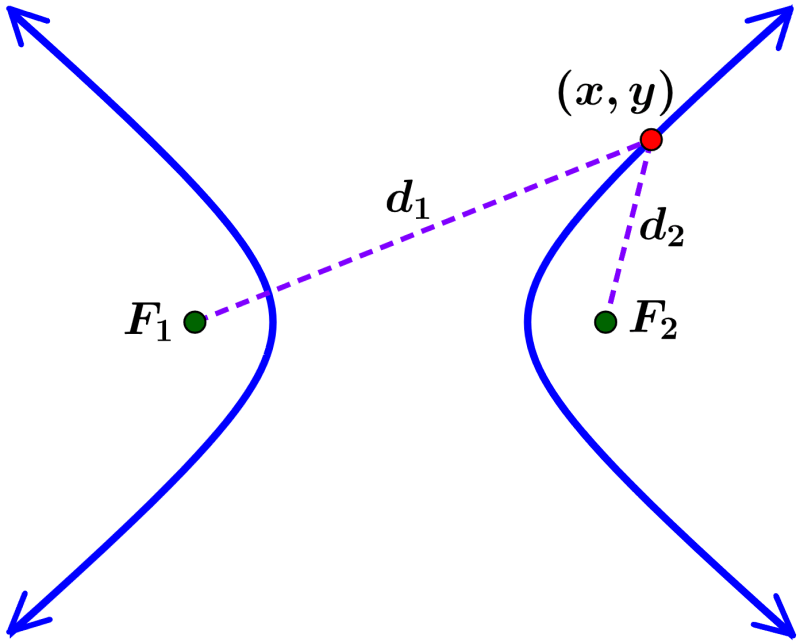
A hyperbola is defined as the set of points so that the difference of the distances to the two foci is a constant. Hyperbolas are made up of two branches, which are a reflection of each other. Each branch of the hyperbola is similar to a parabola and has a focus and a vertex.
Hyperbolas are also defined as conic sections that are obtained at the intersection of a plane with a pair of cones. The plane cuts both bases of the cones at a certain angle.
Main characteristics of a hyperbola
The main characteristics of a hyperbola are:
- Hyperbolas have two focal points, called foci.
- The eccentricity of the hyperbolas is greater than 1.
- The difference of each distance from a point on the hyperbola to the two foci is constant.
- Hyperbolas have two axes of symmetry, one axis passes through the foci and the other axis is perpendicular to the first.
- The intersection of the lines of symmetry is the center of the hyperbola.
- Hyperbolas have two asymptotes, towards which they approach, but never touch.
- The asymptotes also intersect at the center of the hyperbola.
Equation of a hyperbola
The form of the hyperbola equation depends on whether the hyperbola is centered at the origin or centered outside the origin.
When we have a hyperbola centered on the origin, its general equation is:
| $latex \frac{{{x}^2}}{{{a}^2}}-\frac{{{y}^2}}{{{b}^2}}=1$ |
where a represents the length of the segment that extends between the two vertices of the hyperbola and b is found with the equation $latex {{b}^2}={{a}^2}({{e}^2}-1)$, where, e is the eccentricity.
If the center of the hyperbola is located outside the origin, the equation of the hyperbola is:
| $latex \frac{{{(x-h)}^2}}{{{a}^2}}-\frac{{{(y-k)}^2}}{{{b}^2}}=1$ |
where, $latex (h, k)$ are the coordinates of the center of the hyperbola.
See also
Interested in learning more about hyperbolas? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
