Hyperbolas are conic sections formed when a plane intersects a pair of cones. For the hyperbola to be formed, the plane has to intersect both bases of the cones. Hyperbolas are made up of two branches that are shaped like a parabola. We have a vertex and a focus in each branch, which serve to define the hyperbola. We also have two asymptotes, which define the shape of the branches.
The point of intersection of the asymptotes is the center of the hyperbola. Hyperbolas appear on various objects in real life. We can find hyperbolic figures in architecture, in various buildings and structures. We also find hyperbolas in the sonic boom of airplanes and even in the shape of the cooling towers of nuclear plants.
Structures of buildings
Some buildings are shaped like a hyperbolic paraboloid. A hyperbolic paraboloid is a three-dimensional curve that is a hyperbola in one cross-section and a parabola in another cross-section. An example of this is the Washington-Dulles airport in the United States.
There are also buildings that are shaped like an hourglass and contain both branches of the hyperbola. An example of this is the Kobe Port Tower in Japan. The tower is completely symmetrical.
Gear transmission
It is possible to form a gear transmission from hyperbolic gears. The gears have skewed shafts and an hourglass shape that give them the hyperbolic shape. Two hyperboloids can transmit motion between two inclined axles.
Source: Wolfram: Computation Meets Knowledge
Sonic boom
As an airplane moves faster than the speed of sound, a cone-shaped wave is formed. The part of the cone that intersects the ground is a hyperbola. The sonic boom hits every point on that curve at the same time. No sound is heard outside the curve. The hyperbola is known as the “sonic boom curve.”
Cooling towers
The hyperboloid is the standard design for all nuclear power plant cooling towers and some coal-fired power plants. These towers are structurally efficient and can be built with straight steel girders.
The design of cooling towers mainly focuses on two problems:
- The structure must be strong enough to withstand strong winds.
- The towers should be built with the least amount of material possible.
The hyperbolic shape of the cooling towers solves both problems. These towers are very resistant. For a given diameter and height of the tower and for a given force it must withstand, this shape requires less material than any other shape.
Kepler orbits of particles
Kepler orbits are the paths followed by any orbiting body. This can be applied to particles of any size as long as gravity is the only force causing the trajectory. Depending on the orbital properties such as size and eccentricity, this orbit can be any of the four conic sections.
If the eccentricity of the orbit is greater than 1, the trajectory of the object is hyperbolic. In the following figure, the blue line is a hyperbolic orbit. The heaviest object that causes the orbital trajectory is located in one of the foci of the hyperbola.
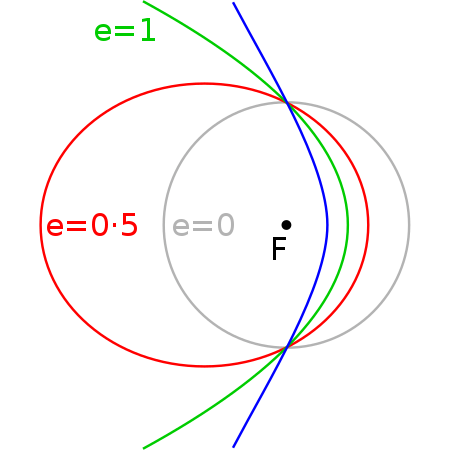
The type of orbit of an object depends on its energy level. Circular or elliptical orbits are closed orbits, which means that the object never escapes its closed path around one of the focal points.
This is because the total energy of the object is less than the minimum energy required to escape and the energy of the object is considered negative in these cases.
A parabolic trajectory has enough energy to escape. However, this is a special case where the total energy of the object is exactly equal to the energy needed to escape, so the energy is considered as zero.
If the object has more energy than is necessary to escape, the trajectory will be hyperbolic. This means that the total energy of the object is positive.
Additional applications
- A guitar is an example of a hyperbola since its sides form the two branches of a hyperbola.
- Satellite systems and radio systems use hyperbolic functions.
- Lenses, monitors, and optical lenses are shaped like a hyperbola.
See also
Interested in learning more about hyperbolas? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
