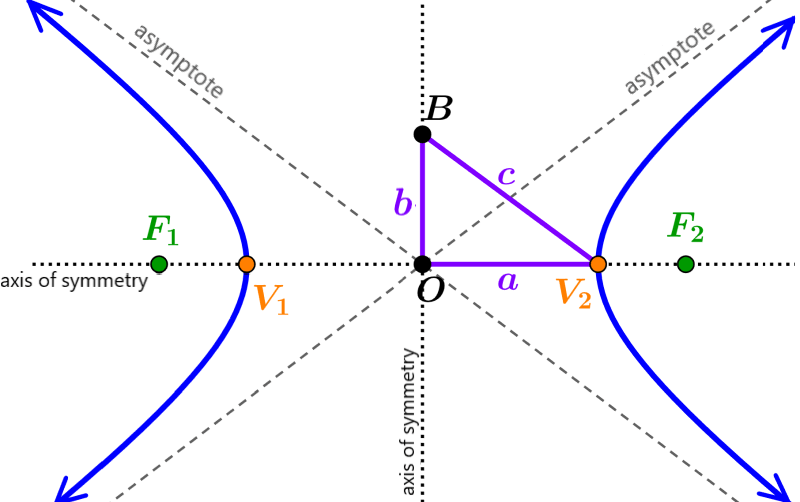
The asymptotes of a hyperbola are straight lines that the curve approaches as the values of the independent variable (x) increase. The branches of the hyperbola approach the asymptotes but never touch them. All hyperbolas have two asymptotes, which intersect at the center of the hyperbola. The equations of the asymptotes can have four different variations depending on the location of the center and the orientation of the hyperbola.
Here, we will explore the equations of hyperbolas along with some practice exercises.
Asymptotes of hyperbolas centered at the origin
Hyperbolas centered on the origin can be oriented horizontally or vertically. Depending on this, the equation of a hyperbola will be different.
Recall that a hyperbola that is centered at the origin and horizontally oriented has the equation:
$latex \frac{{{x}^2}}{{{a}^2}}-\frac{{{y}^2}}{{{b}^2}}=1$
where a is the length of the distance from the center to a vertex and b is the length of the distance from the center to the co-vertex. This equation applies when the transverse axis (segment connecting the vertices) is on the x-axis.
In this case, the equations of the asymptotes are:
$latex y=\pm \frac{b}{a}x$
When the hyperbola is centered at the origin and oriented vertically, its equation is:
$latex \frac{{{y}^2}}{{{a}^2}}-\frac{{{x}^2}}{{{b}^2}}=1$
This equation applies when the transverse axis is on the y axis. In this case, the equations of the asymptotes are:
$latex y=\pm \frac{a}{b}x$
Asymptotes of hyperbolas centered outside the origin
When the hyperbola is centered outside the origin, we can apply translations to obtain a new equation. If the hyperbola is oriented horizontally, its equation is:
$latex \frac{{{(x-h)}^2}}{{{a}^2}}-\frac{{{(y-k)}^2}}{{{b}^2}}=1$
where h is the x coordinate of the center and k is the y coordinate of the center. This equation applies when the transverse axis (segment connecting the vertices) is parallel to the x-axis. The equations of the asymptotes in this case are:
$latex y-k=\pm \frac{b}{a}(x-h)$
On the other hand, if the hyperbola is oriented vertically, its equation is:
$latex \frac{{{(y-k)}^2}}{{{a}^2}}-\frac{{{(x-h)}^2}}{{{b}^2}}=1$
This equation applies when the transverse axis is parallel to the y axis. The equations of the asymptotes in this case are:
$latex y-k=\pm \frac{a}{b}(x-h)$
Asymptotes of hyperbolas – Examples with answers
With the following examples, you can analyze the process used to find the equations of the asymptotes of hyperbolas. Each example has its respective solution, but it is recommended that you try to solve the problems yourself before looking at the answer.
EXAMPLE 1
What is the equation of the asymptotes of the hyperbola $latex \frac{{{x}^2}}{36}-\frac{{{y}^2}}{16}=1$?
Solution
We can see that the equation has the form $latex \frac{{{x}^2}}{{{a}^2}}-\frac{{{y}^2}}{{{b}^2}}=1$. This means that the hyperbola is centered at the origin and is oriented horizontally. Therefore, the equation of its asymptotes is:
$latex y=\pm \frac{b}{a}x$
From the equation, we identify the following values:
$latex {{a}^2}=36$
$latex a=6$
$latex {{b}^2}=16$
$latex b=4$
Substituting these values into the equation of the asymptotes, we have:
$latex y=\pm \frac{4}{6}x$
$latex y=\pm \frac{2}{3}x$
EXAMPLE 2
If a hyperbola has the equation $latex \frac{{{y}^2}}{25}-\frac{{{x}^2}}{9}=1$, what are its asymptotes?
Solution
In this case, the equation has the form $latex \frac{{{y}^2}}{{{a}^2}}-\frac{{{x}^2}}{{{b}^2}}=1$. Therefore, the hyperbola is centered at the origin and oriented vertically. Therefore, the equation of its asymptotes is:
$latex y=\pm \frac{a}{b}x$
From the equation, we identify the following values:
$latex {{a}^2}=25$
$latex a=5$
$latex {{b}^2}=9$
$latex b=3$
Using these values in the equation of the asymptotes, we have:
$latex y=\pm \frac{5}{3}x$
EXAMPLE 3
What is the equation of the asymptotes of the hyperbola $latex \frac{{{(x-2)}^2}}{64}-\frac{{{(y-3)}^2}}{25}=1$?
Solution
The equation of the hyperbola has the form $latex \frac{{{(x-h)}^2}}{{{a}^2}}-\frac{{{(y-k)}^2}}{{{b}^2}}=1$. This hyperbola is centered on (h, k) and is oriented horizontally. Therefore, the equation of its asymptotes is:
$latex y-k=\pm \frac{b}{a}(x-h)$
We have the following values:
$latex {{a}^2}=64$
$latex a=8$
$latex {{b}^2}=25$
$latex b=5$
Using these values into the equation for the asymptotes, we have:
$latex y-3=\pm \frac{5}{8}(x-2)$
$latex y=\pm \frac{5}{8}(x-2)+3$
EXAMPLE 4
f a hyperbola has the equation $latex \frac{{{(y+5)}^2}}{25}-\frac{{{(x-2)}^2}}{9}=1$, what are its asymptotes?
Solution
In this case, we have the form $latex \frac{{{(y-k)}^2}}{{{a}^2}}-\frac{{{(x-h)}^2}}{{{b}^2}}=1$. Therefore, we have the center at (h, k) and the hyperbola is oriented vertically. Therefore, the equation of its asymptotes is:
$latex y-k=\pm \frac{a}{b}(x-h)$
We have the following values:
$latex {{a}^2}=25$
$latex a=5$
$latex {{b}^2}=9$
$latex b=3$
We substitute these data into the equation of the asymptotes:
$latex y+5=\pm \frac{5}{3}(x-2)$
$latex y=\pm \frac{5}{3}(x-2)-5$
Asymptotes of hyperbolas – Practice problems
Solve the following problems to practice what you have learned about hyperbola asymptotes. If you need help with this, you can look at the solved examples above for guidance.
See also
Interested in learning more about hyperbolas? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
