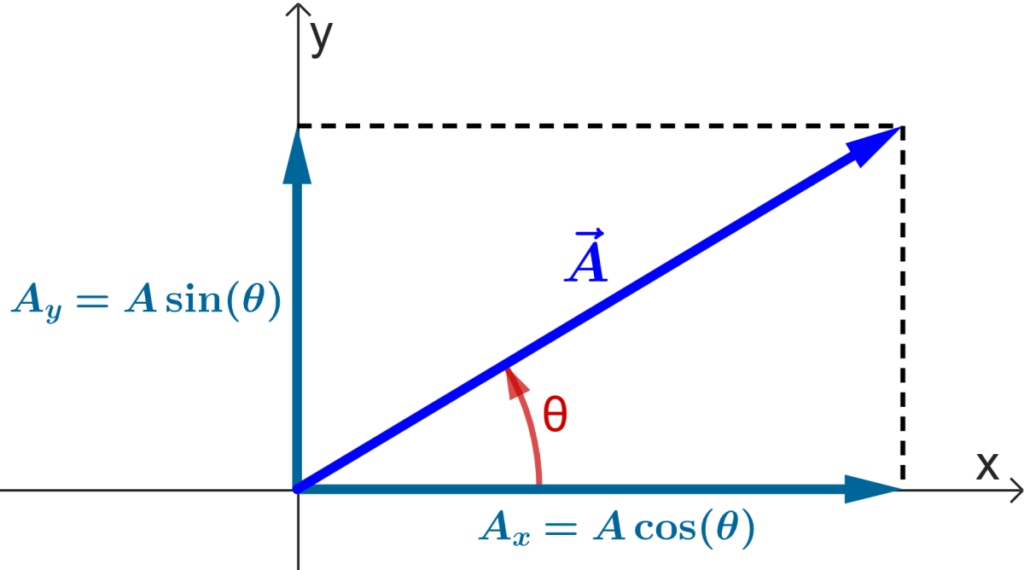
The components of a vector are scalar quantities that indicate the “displacement” on each axis of a coordinate system. These components can be calculated using the magnitude and direction of the vector, along with the fundamental trigonometric functions.
Here, we will learn how to find the components of a vector. Also, we will look at some applications of the components and practice examples.
What are the components of a vector?
The components of a vector are the numbers that indicate the displacement in the direction of each axis of a coordinate system.
We can obtain a clearer definition of the components of a vector $latex \vec{A}$ by plotting it to a Cartesian coordinate system, as shown in the following diagram:
If we assume that $latex \vec{A}$ is a displacement vector, we can consider $latex \vec{A}$ as the sum of a displacement parallel to the $latex x$-axis and a displacement parallel to the $latex y$-axis.
We use the notation $latex A_{x}$ and $latex A_{y}$ to indicate the amount of displacement on the $latex x$-axis and $latex y$-axis respectively.
The two numbers $latex A_{x}$ and $latex A_{y}$ are the components of $latex \vec{A}$. These numbers can be positive or negative.
EXAMPLE
If a vector $latex \vec{A}$ is the addition of a displacement of 10 m to the East (positive x-axis) and 20 m to the North (positive y-axis), its components are:
$latex A_{x}=10\text{ m}$
$latex A_{y}=20\text{ m}$
Note that the components are not vectors. The components of a vector are numbers and not vectors. For this reason, we use letters without arrows above them to represent them.
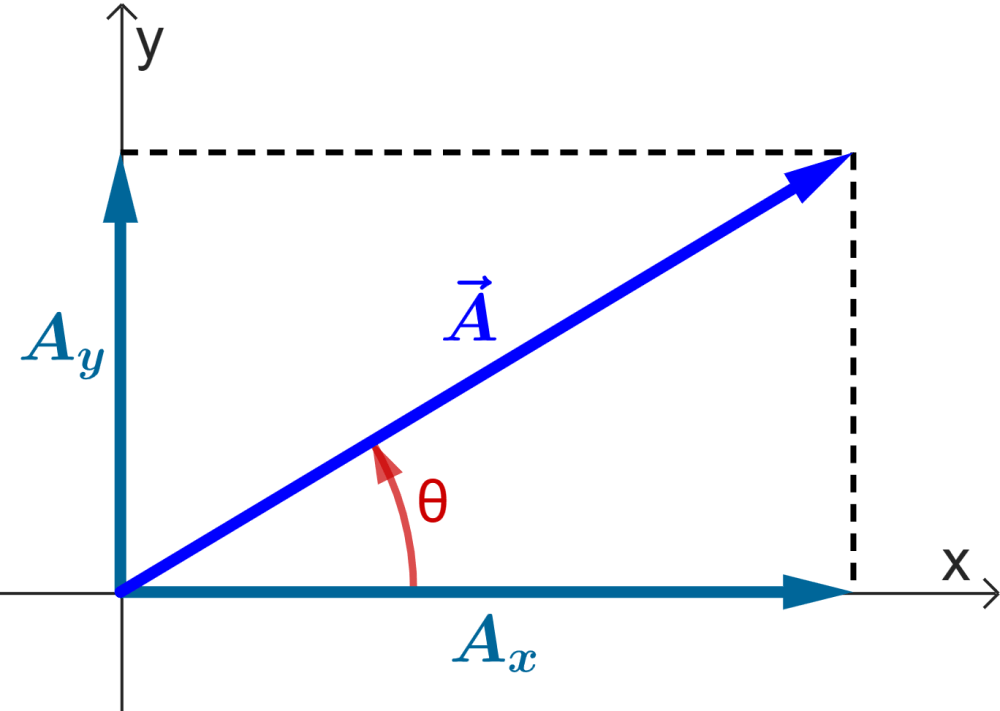
Formulas for finding the components of a vector
To calculate the components of a vector $latex \vec{A}$, we need to know its magnitude $latex A$ and its direction.
The direction of the vector is described by an angle measured from the positive x-axis. The angle is positive when it goes counterclockwise.
Consider the following diagram to find the formulas of the components of a vector:
Recalling that the cosine in a right triangle is equal to the adjacent side on the hypotenuse and the sine is equal to the opposite side on the hypotenuse, we have:
$$\frac{A_{x}}{A}=\cos(\theta)\text{ and }\frac{A_{y}}{A}=\sin(\theta)$$
Then, the formulas for the components of a vector are:
$latex A_{x}=A\cos(\theta)$
$latex A_{y}=A\sin(\theta)$
These equations are correct only when the angle θ is measured from the positive x-axis. If the vector angle has a different reference, the relationships will be different.
10 Solved examples on the components of a vector
EXAMPLE 1
If the vector $latex \vec{A}$ has a magnitude of 100 mm and an angle of 60° with respect to the $latex x$ axis, what are its components $latex x$ and $latex y$?
Solution
We have the following data
- Magnitude: $latex A=100$ mm
- Angle: $latex \theta=60^{\circ}$
- $latex \cos(60^{\circ})=0.5$
- $latex \sin(60^{\circ})=0.866$
Then, we use the formulas for the components of a vector with the given data:
$latex A_{x}=A\cos(\theta)$
$latex =100\cos(60^{\circ})$
$latex =50$ mm
$latex A_{y}=A\sin(\theta)$
$latex =100\sin(60^{\circ})$
$latex =86.6$ mm
EXAMPLE 2
Find the $latex x$ and $latex y$ components of the vector $latex \vec{B}$ having a magnitude of 15 units and an angle of 60° with respect to the $latex x$ axis.
Solution
We can observe the following information:
- Magnitude: $latex B=15$
- Angle: $latex \theta=60^{\circ}$
- $latex \cos(60^{\circ})=0.5$
- $latex \sin(60^{\circ})=0.866$
Applying the formulas for the components of a vector with the given information, we have:
$latex B_{x}=B\cos(\theta)$
$latex =15\cos(60^{\circ})$
$latex =7.5$
$latex B_{y}=B\sin(\theta)$
$latex =15\sin(60^{\circ})$
$latex \approx 13$
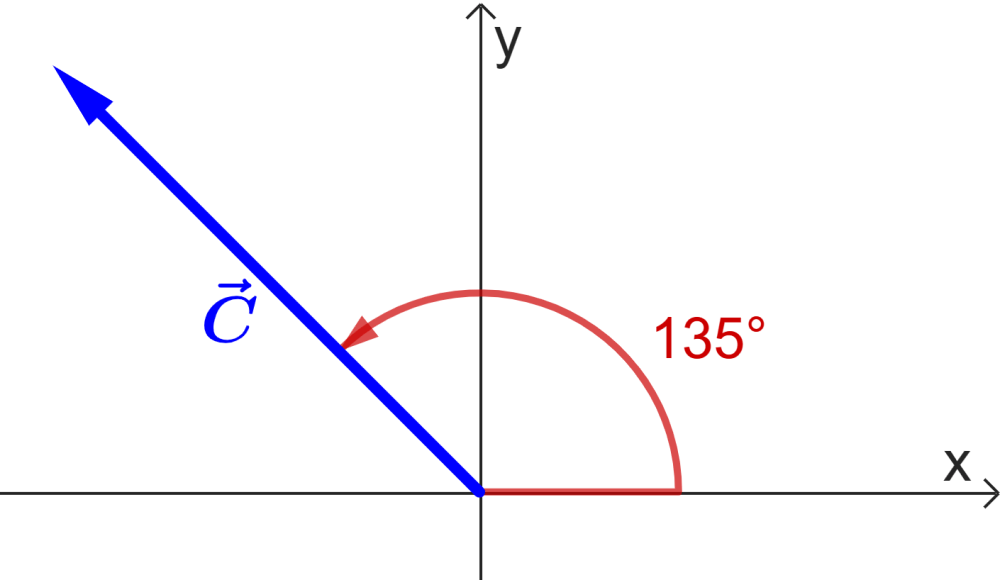
EXAMPLE 3
The vector $latex \vec{C}$ has a magnitude of 20 units and an angle of 135° with respect to the $latex x$ axis. Find its components $latex x$ and $latex y$.
Solution
From the question, we have:
- Magnitude: $latex C=20$
- Angle: $latex \theta=135^{\circ}$
- $latex \cos(135^{\circ})=-0.7071$
- $latex \sin(135^{\circ})=0.7071$
Now, we can calculate the components:
$latex C_{x}=C\cos(\theta)$
$latex =20\cos(135^{\circ})$
$latex =-14.142$
$latex C_{y}=C\sin(\theta)$
$latex =20\sin(135^{\circ})$
$latex =14.142$
We can clearly see that the $latex x$ component is negative and the $latex y$ component is positive:
.
EXAMPLE 4
If the vector $latex \vec{A}$ has a magnitude of 18 units and an angle of 120° with respect to the $latex x$ axis, what are its components $latex x$ and $latex y$?
Solution
We can obtain the following information:
- Magnitude: $latex A=18$
- Angle: $latex \theta=120^{\circ}$
- $latex \cos(120^{\circ})=-0.5$
- $latex \sin(120^{\circ})=0.866$
Then, we use the formulas for the components of a vector with the given data:
$latex A_{x}=A\cos(\theta)$
$latex =18\cos(120^{\circ})$
$latex =-9$
$latex A_{y}=A\sin(\theta)$
$latex =18\sin(120^{\circ})$
$latex =15.588$
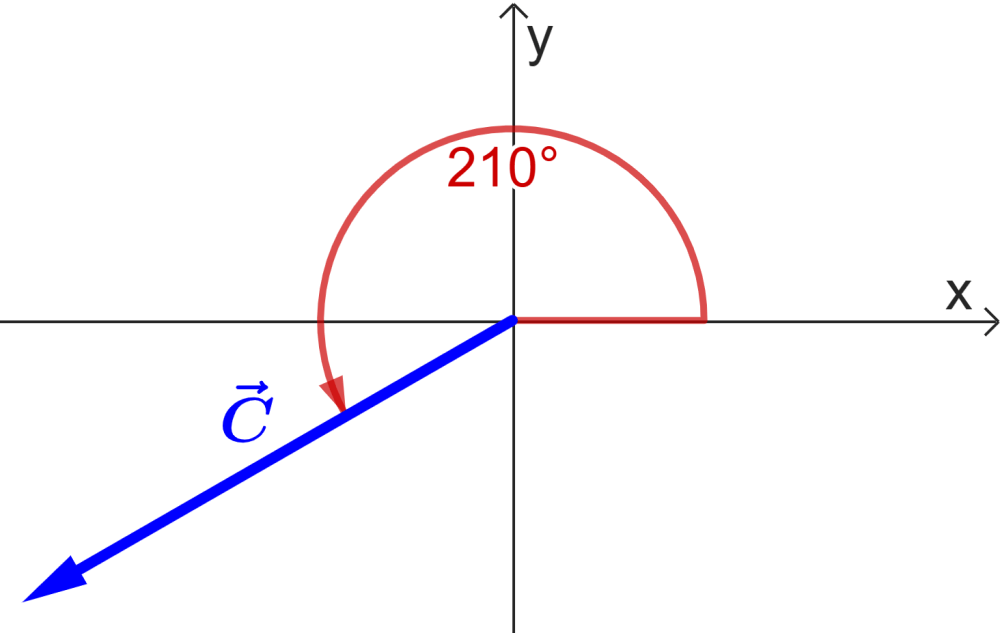
EXAMPLE 5
Find the components of the vector $latex \vec{B}$ which has a magnitude of 30 units and an angle of 210° with respect to the $latex x$-axis.
Solution
We can extract the following information:
- Magnitude: $latex B=30$
- Angle: $latex \theta=210^{\circ}$
- $latex \cos(210^{\circ})=-0.8660$
- $latex \sin(210^{\circ})=-0.5$
Then, we use the formulas for the components of a vector with the given data:
$latex B_{x}=B\cos(\theta)$
$latex =30\cos(120^{\circ})$
$latex =-25.98$
$latex B_{y}=B\sin(\theta)$
$latex =30\sin(120^{\circ})$
$latex =-15$
We can observe that both components are negative:
.
EXAMPLE 6
The vector $latex \vec{C}$ has a magnitude of 40 units and an angle of 150° with respect to the $latex x$-axis. Find its components.
Solution
We can observe the following:
- Magnitude: $latex C=40$
- Angle: $latex \theta=150^{\circ}$
- $latex \cos(150^{\circ})=-0.8660$
- $latex \sin(150^{\circ})=0.5$
We find the components using the standard formulas:
$latex C_{x}=C\cos(\theta)$
$latex =40\cos(150^{\circ})$
$latex =-34.64$
$latex C_{y}=C\sin(\theta)$
$latex =40\sin(150^{\circ})$
$latex =20$
EXAMPLE 7
Find the components of the following vector:
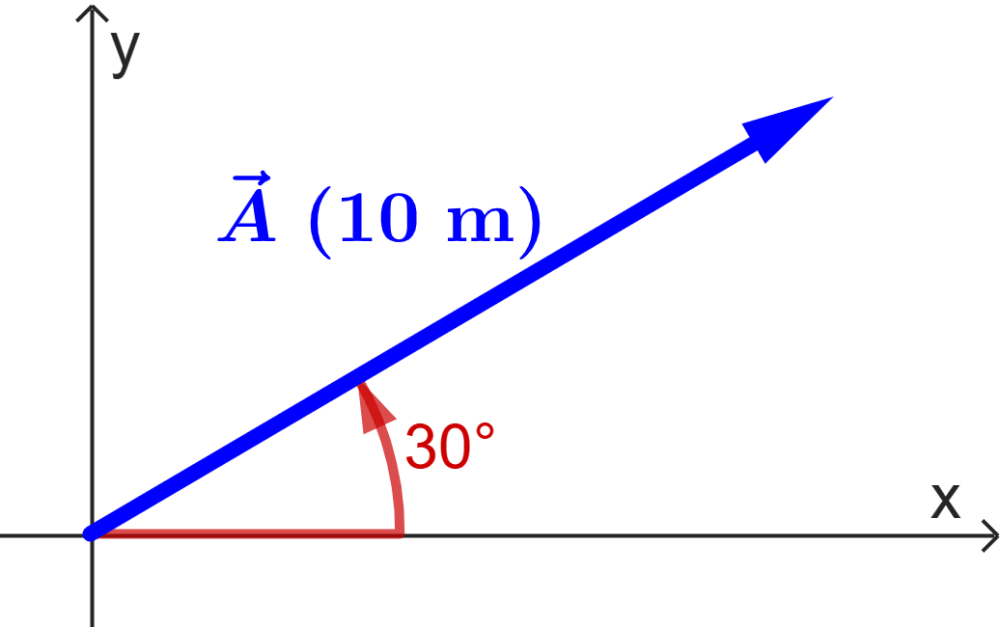
Solution
We can start by writing down the information we know:
- Magnitude: $latex A=10$ m
- Angle: $latex \theta=30^{\circ}$
Now, we use the formulas for the components:
$latex A_{x}=A\cos(\theta)$
$latex =10\cos(30^{\circ})$
$latex =8.66$ m
$latex A_{y}=A\sin(\theta)$
$latex =10\sin(30^{\circ})$
$latex =5$ m
EXAMPLE 8
What are the components of the following vector?
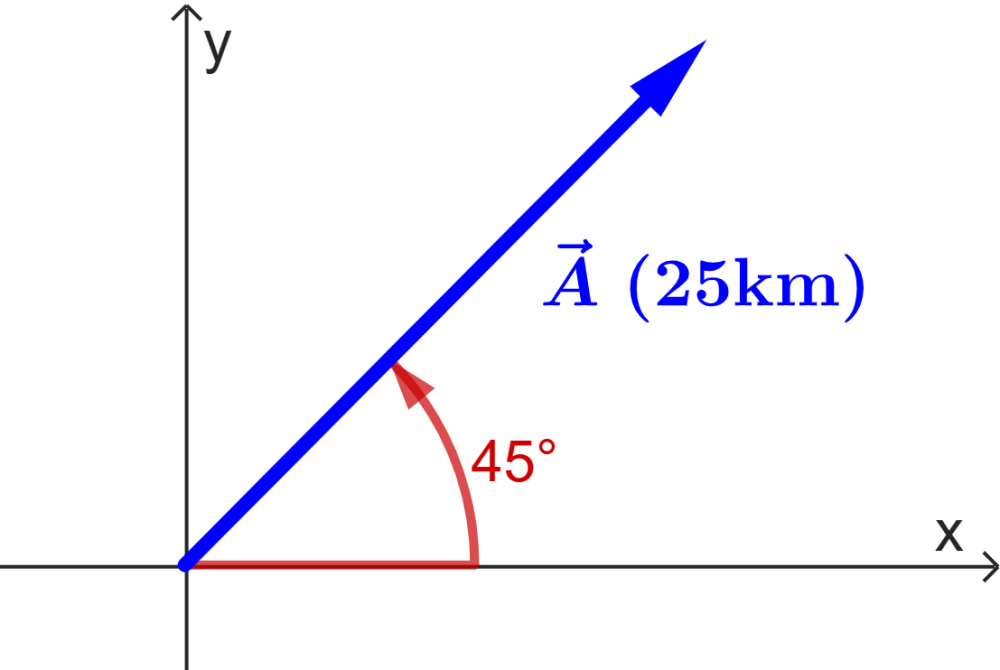
Solution
We have the following information:
- Magnitude: $latex A=25$ km
- Angle: $latex \theta=45^{\circ}$
Therefore, we have:
$latex A_{x}=A\cos(\theta)$
$latex =25\cos(45^{\circ})$
$latex =17.678$ km
$latex A_{y}=A\sin(\theta)$
$latex =25\sin(45^{\circ})$
$latex =17.678$ km
EXAMPLE 9
Determine the components of the following vector:
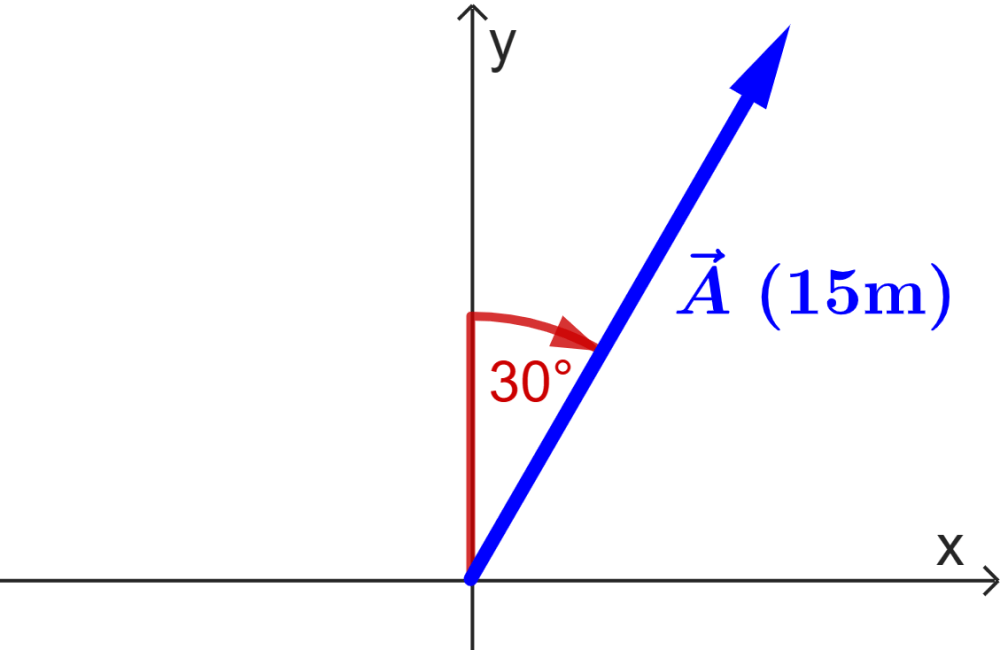
Solution
We see that in this case, the angle is measured from the y-axis and clockwise:
- $latex A=15$ m
- $latex \theta=30^{\circ}$
We can use trigonometry to find other equations with this angle, or we can use the original equations and find an equivalent angle from the positive x-axis.
Let’s use the given angle and trigonometry to find the following:
$latex A_{x}=A\sin(\theta)$
$latex =15\sin(30^{\circ})$
$latex =7.5$ m
$latex A_{y}=A\cos(\theta)$
$latex =15\cos(30^{\circ})$
$latex =12.99$ m
EXAMPLE 10
What are the components of the following vector?
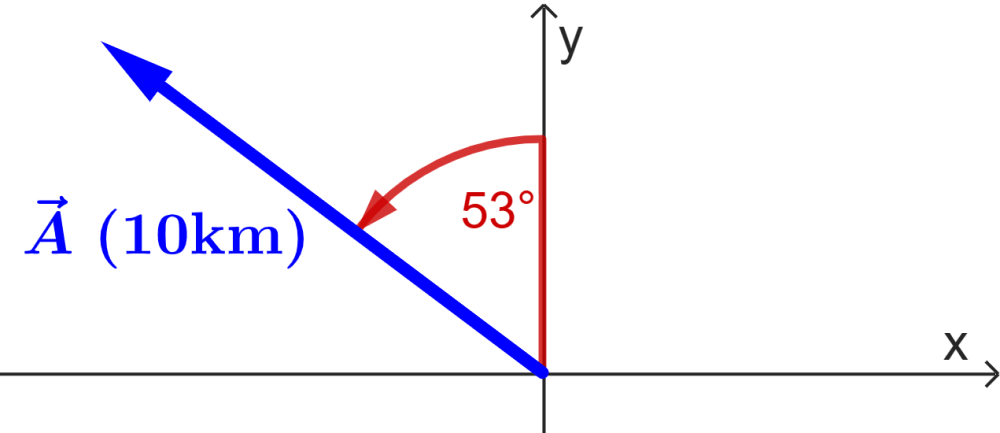
Solution
We can use the same process as the previous example, or we can find the angle measured from the positive x-axis.
Note that the angle is measured from the positive y-axis in the counterclockwise direction. If we add 90°, we will find its equivalent angle from the positive x-axis:
- $latex A=10$ km
- $latex \theta=53^{\circ}+90^{\circ}=143^{\circ}$
Therefore, we have:
$latex A_{x}=A\cos(\theta)$
$latex =10\cos(143^{\circ})$
$latex =-7.986$ km
$latex A_{y}=A\sin(\theta)$
$latex =10\sin(143^{\circ})$
$latex =6.018$ km
In this case, the x component is negative because the vector is in the second quadrant.
Components of vectors – Practice problems
What is the $latex x$ component of a vector that has a magnitude of 1259 units and an angle of 270° with respect to the $latex x$ axis?
Write the answer in the input box.
See also
Interested in learning more about vectors? You can look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
