In physics, understanding motion is fundamental, and no comprehension of motion is complete without delving into the concept of acceleration. Average acceleration is the rate at which an object changes its velocity over a specific period of time. It is a vector quantity, meaning it has both magnitude and direction.
In this article, we will explore the concept of average acceleration in detail, making it accessible and understandable. We will look at its formula, examples, and common misconceptions.
What is Average Acceleration in Physics?
In physics, average acceleration is defined as the total change of velocity over a given time period. It’s a measure of how quickly an object changes its velocity.
Acceleration is a vector quantity, meaning it has both magnitude and direction. Therefore, average acceleration is also a vector quantity.
Average acceleration is measured in units of distance over time squared, such as meters per second squared ($latex \frac{\text{m}}{\text{s}^2}$), miles per hour squared ($latex \frac{\text{mi}}{\text{h}^2}$) or kilometers per hour squared ($latex \frac{\text{km}}{\text{h}^2}$).
Mathematically, average acceleration ($latex a_{avg}$) is calculated by dividing the change in velocity ($latex \Delta v$) by the change in time ($latex \Delta t$).
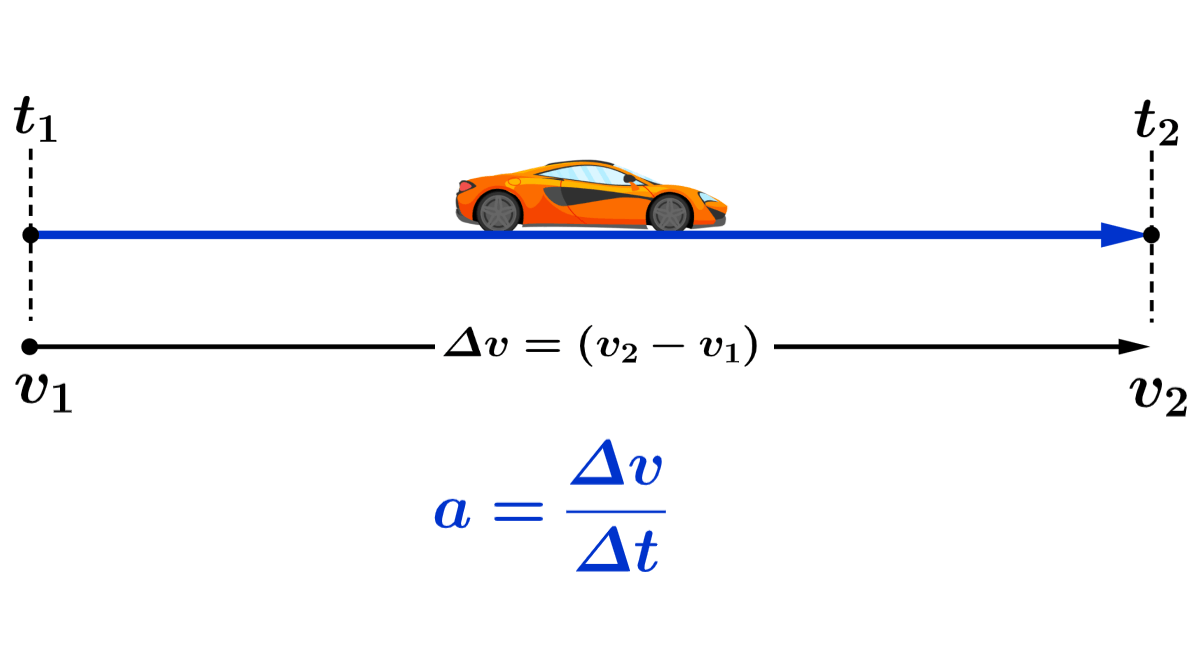
Typical Average Acceleration of Common Objects
| Object/Scenario | Average Acceleration (m/s²) |
|---|---|
| Freefall near the Earth’s surface | 9.8 (due to gravity) |
| Car accelerating from rest | 1 to 3 |
| Space shuttle during launch | 29.4 |
| Subway train accelerating from rest | 1.1 |
| Elevator starting to ascend | 1 to 2 |
| A sprinter starting a 100m dash | 8 to 10 |
| Commercial jet during takeoff | 3 |
These magnitudes are approximations and can vary significantly in different situations. The units are in meters per second squared (m/s²), which is the standard unit of acceleration.
Average Acceleration Formula and Calculation
Average acceleration is a measure of the rate at which an object changes its velocity that can be calculated using the following formula:
$$a_{avg} = \frac{\Delta v}{\Delta t}$$
Where:
- $latex \Delta v$ represents the change in velocity, and
- $latex \Delta t$ represents the time period over which this change occurs.
Recall that acceleration is a vector quantity, meaning it has both magnitude and direction. Generally, we specify average acceleration in a given axis, like the $latex x$ or $latex y$ axis.
If velocity is expressed in meters per second and time is expressed in seconds, then average acceleration is in meters per second squared ($latex \frac{\text{m}}{\text{s}^2}$).
Step-by-step calculation
Now, let’s go through the step-by-step process of calculating average acceleration.
Step 1: Identify the initial and final velocities, $latex v_{i}$ y $latex v_{f}$, respectively.
Step 2: Calculate $latex \Delta v=v_{f}-v_{i}$.
Step 3: Identify the time over which the change in velocity occurred. This is $latex \Delta t$.
Step 4: Divide $latex \Delta v$ by $latex \Delta t$ to get average acceleration.
Remember, this is the average acceleration. It assumes that the car’s acceleration was constant over this time period, which may not always be the case in real-world scenarios.
Average Acceleration – Examples with Answers
EXAMPLE 1
A car starts from rest and reaches a speed of 60 m/s in 10 seconds. What is its average acceleration?
Solution
The formula for average acceleration is:
$$a_{avg}=\frac{v_f-v_i}{\Delta t}$$
where:
- $latex a_{avg}$ is the average acceleration
- $latex v_f$ is the final velocity
- $latex v_i$ is the initial velocity
- $latex \Delta t$ is the change in time
Here, $latex v_i = 0$ m/s (because the car starts from rest), $latex v_f = 60$ m/s, and $latex \Delta t = 10$ s. Plugging in these values gives:
$$a_{avg}=\frac{60-0}{10}$$
$latex a_{avg}=6~\frac{\text{m}}{\text{s}^2}$
Therefore, the car’s average acceleration is 6 m/s².
EXAMPLE 2
A train slows down from 40 m/s to 20 m/s in 5 seconds. What is its average acceleration?
Solution
Using the same formula:
$$a_{avg} = \frac{v_f – v_i}{\Delta t}$$
In this case, $latex v_i = 40$ m/s, $latex v_f = 20$ m/s, and $latex \Delta t = 5$ s. Plugging in these values gives:
$$a_{avg}=\frac{20-40}{5}$$
$latex a_{avg}=-4~\frac{\text{m}}{\text{s}^2}$
The negative sign indicates that the train is decelerating, or slowing down. Then, the train’s average acceleration (or deceleration, in this case) is -4 m/s².
EXAMPLE 3
A bicycle is moving at a velocity of 12 m/s and then comes to a stop over a time period of 4 seconds. What is the average acceleration?
Solution
We use the same formula again:
$$a_{avg} = \frac{Δv }{Δt}$$
In this case:
- $latex \Delta v =$ final velocity – initial velocity = 0 m/s – 12 m/s = -12 m/s
- $latex \Delta t =$ final time – initial time = 4 s – 0 s = 4 s
Substituting these values in:
$$a_{avg} = \frac{-12}{ 4} = -3~\text{m/s}^2$$
In this case, the acceleration is negative, indicating a deceleration (the bike is slowing down). The average deceleration of the bike is 3 m/s².
EXAMPLE 4
A rocket takes off and reaches a speed of 1000 m/s in 50 seconds. What is its average acceleration?
Solution
We use the following formula:
$$a_{avg} = \frac{v_f – v_i}{\Delta t}$$
Here we have, $latex v_i = 0$ m/s (assuming the rocket starts from rest), $latex v_f = 1000$ m/s, and $latex \Delta t = 50$ s:
$$a_{avg}=\frac{1000-0}{50}$$
$latex a_{avg}=20~\frac{\text{m}}{\text{s}^2}$
Therefore, the rocket’s average acceleration is 20 m/s².
Common Misconceptions About Average Acceleration
Understanding the following misconceptions can help deepen our knowledge of average acceleration and avoid errors when applying this concept in physics problems.
Misconception 1: Average acceleration is always in the direction of motion
The direction of average acceleration is determined by the change in velocity, not just the direction of motion. If an object slows down (decelerates), the acceleration is in the opposite direction of the motion. Therefore, it’s entirely possible for an object to be moving in one direction while its acceleration is in the opposite direction.
Misconception 2: Zero acceleration means the object is at rest
Zero acceleration actually means that the velocity of the object is not changing over time, not that the object is at rest. An object in motion can continue moving at a constant speed and direction (meaning it has zero acceleration) without being at rest.
Misconception 3: Average acceleration and instantaneous acceleration are the same
Average acceleration is calculated over a time interval and can give a general picture of how the velocity changes over that period. On the other hand, instantaneous acceleration is the acceleration at a specific moment in time and could be different from the average acceleration if the acceleration is not constant.
A negative acceleration always means slowing down
While it’s true that a negative acceleration can represent deceleration, it’s also true that it can represent acceleration to the left or downward (in a standard coordinate system), depending on the context. The sign of acceleration is about direction, not just about speeding up or slowing down.
Misconception 5: Average acceleration is always constant
Average acceleration is the average rate of change of velocity with respect to time over a specific interval. It doesn’t mean that the acceleration was constant during that time interval. A constant acceleration would mean that the object’s velocity is changing at a constant rate, but this is a specific case and not always the situation in real-world scenarios.
See also
Interested in learning more about velocity and acceleration? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
