Matrix scalar multiplication is an essential operation in linear algebra and is used in various fields. To solve a matrix multiplication by a scalar, we simply multiply each entry or element of the matrix by the scalar.
In this article, we will explore the concept of scalar multiplication and how it works. We will also solve several exercises to apply the concepts learned.
LINEAR ALGEBRA
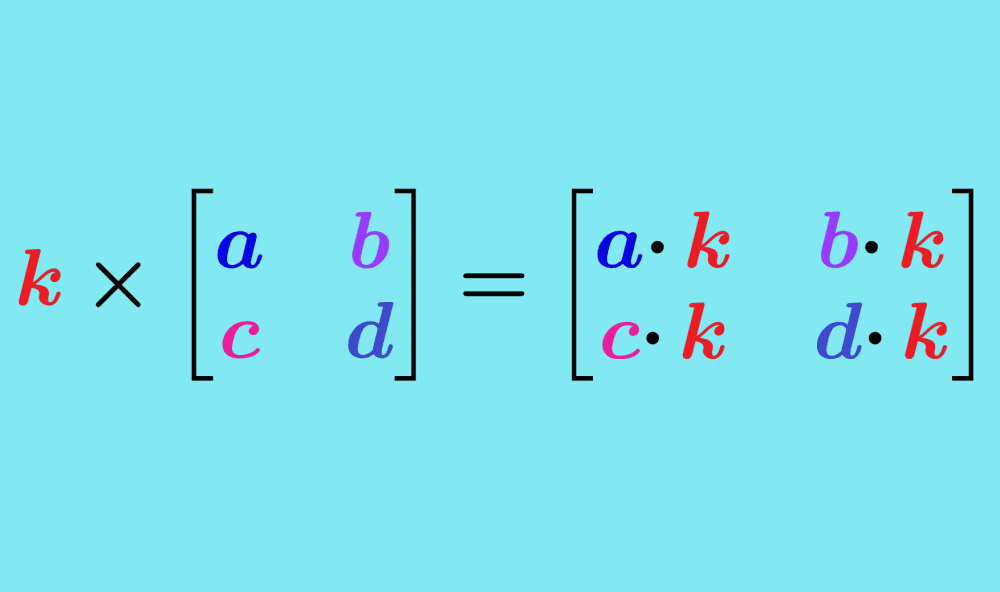
Relevant for…
Learning about the multiplication of matrices by a scalar.
LINEAR ALGEBRA
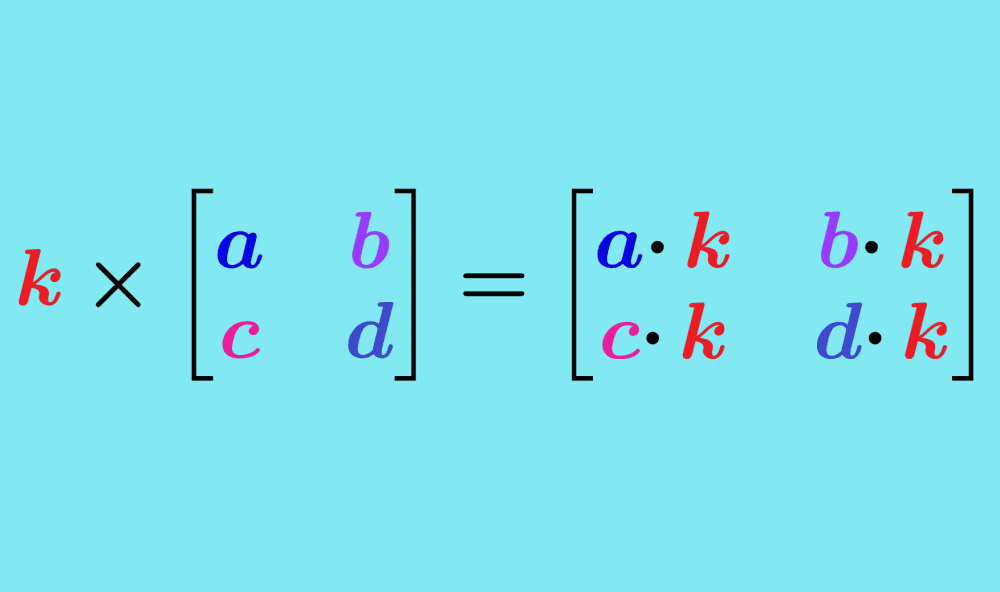
Relevant for…
Learning about the multiplication of matrices by a scalar.
How to multiply matrices by a scalar?
To multiply a matrix by a scalar, we just multiply each element of the matrix by the scalar.
The following is the general formula for scalar multiplication of a matrix:
Given a scalar “k” and an “m x n” matrix A, the scalar multiplication of $latex A$ by $latex k$ is defined as:
$$ k \times A = [k \times a_{ij}]$$
where $latex i = 1,~2,~…,~m$ and $latex j = 1,~2,~…,~n$
In other words, each element $latex a_{ij}$ of the matrix $latex A$ is multiplied by the scalar $latex k$, resulting in a new matrix with the same dimensions as A.
Let’s look at an example to better understand this concept:
Suppose we have the matrix $latex A = \begin{bmatrix} 2 & 3 \ 4 & 5 \end{bmatrix}$ and we want to multiply it by the scalar $latex k = 2$. The resulting matrix will be:
$$k \times A = 2 \times \begin{bmatrix} 2 & 3 \\ 4 & 5 \end{bmatrix}$$
$$ = \begin{bmatrix} 2\times 2 & 2\times 3 \\ 2\times 4 & 2\times 5\end{bmatrix}$$
$$ = \begin{bmatrix} 4 & 6 \\ 8 & 10 \end{bmatrix}$$
Solved exercises on matrix multiplication by a scalar
EXAMPLE 1
Find the result of the multiplication of the following 2×2 matrix by $latex k=4$:
$$A = \begin{pmatrix} 3 & 5 \\ 7 & 2 \end{pmatrix}$$
Solution
To multiply a matrix by a scalar, multiply each element of the matrix by the scalar.
Given the matrix $latex A = \begin{pmatrix} 3 & 5 \\ 7 & 2 \end{pmatrix}$ and the scalar $latex k=4$, we perform the following operations:
- Multiply the first element (top left) of the matrix by $latex k$: $latex 3 \times 4 = 12$.
- Multiply the second element (upper right) of the matrix by $latex k$: $latex 5 \times 4 = 20$.
- Multiply the third element (bottom left) of the matrix by $latex k$: $latex 7 \times 4 = 28$.
- Multiply the fourth element (bottom right) of the matrix by $latex k$: $latex 2 \times 4 = 8$.
Now, we can construct the resulting matrix by placing the results of these multiplications in their respective positions:
$$A’ = \begin{pmatrix} 12 & 20 \\ 28 & 8 \end{pmatrix}$$
EXAMPLE 2
Multiply the matrix B by the scalar $latex m=2$:
$$B = \begin{pmatrix} 6 & -3 \\ 1 & 4 \end{pmatrix}$$
Solution
In the previous example, we looked at how to solve this type of multiplication step by step. Now, let’s simplify this process.
Distribute the scalar multiplication by multiplying each element of the matrix by $latex m$:
$$2 \times \begin{pmatrix} 6 & -3 \\ 1 & 4 \end{pmatrix}$$
$$= \begin{pmatrix} 2\times6 & 2\times(-3) \\ 2\times1 & 2\times4 \end{pmatrix}$$
$$= \begin{pmatrix} 12 & -6 \\ 2 & 8 \end{pmatrix}$$
EXAMPLE 3
Find the result of multiplying the following matrix by the scalar $latex n=-3$:
$$C = \begin{pmatrix} 0 & 9 \\ -5 & 3 \end{pmatrix}$$
Solution
Perform scalar multiplication by multiplying each element of the matrix by $latex n$:
$$-3 \times \begin{pmatrix} 0 & 9 \\ -5 & 3 \end{pmatrix}$$
$$ = \begin{pmatrix} -3\times0 & -3\times9 \\ -3\times(-5) & -3\times3 \end{pmatrix}$$
$$ = \begin{pmatrix} 0 & -27 \\ 15 & -9 \end{pmatrix}$$
EXAMPLE 4
If we multiply the following matrix by the scalar $latex p=3$, what is the result?
$$D = \begin{pmatrix} 2 & 4 & 6 \\ 1 & 3 & 5 \\ 0 & 1 & 7 \end{pmatrix}$$
Solution
In this case, we have a 3×3 matrix, but the process to solve the multiplication is the same. We just have to distribute the multiplication to each element:
$$3 \times \begin{pmatrix} 2 & 4 & 6 \\ 1 & 3 & 5 \\ 0 & 1 & 7 \end{pmatrix}$$
$$ = \begin{pmatrix} 3\times2 & 3\times4 & 3\times6 \\ 3\times1 & 3\times3 & 3\times5 \\ 3\times0 & 3\times1 & 3\times7 \end{pmatrix}$$
$$ = \begin{pmatrix} 6 & 12 & 18 \\ 3 & 9 & 15 \\ 0 & 3 & 21 \end{pmatrix}$$
EXAMPLE 5
Multiply the 3×3 matrix by the scalar $latex q=-2$:
$$E = \begin{pmatrix} -2 & 5 & 1 \\ 0 & 3 & 6 \\ 8 & -4 & 2 \end{pmatrix}$$
Solution
Multiply each element of the matrix E by the scalar $latex q=-2$:
$$-2 \times \begin{pmatrix} -2 & 5 & 1 \\ 0 & 3 & 6 \\ 8 & -4 & 2 \end{pmatrix}$$
$$ = \begin{pmatrix} -2\times(-2) & -2\times5 & -2\times1 \\ -2\times0 & -2\times3 & -2\times6 \\ -2\times8 & -2\times(-4) & -2\times2 \end{pmatrix}$$
$$ = \begin{pmatrix} 4 & -10 & -2 \\ 0 & -6 & -12 \\ -16 & 8 & -4 \end{pmatrix}$$
EXAMPLE 6
Multiply the matrix F by the scalar $latex r=0.5$:
$$F = \begin{pmatrix} 9 & 6 & 3 \\ 5 & 7 & 1 \\ 4 & 8 & 2 \end{pmatrix}$$
Solution
Distributing the multiplication of the scalar $latex r=0.5$ to each element of the matrix F, we have:
$$0.5 \times \begin{pmatrix} 9 & 6 & 3 \\ 5 & 7 & 1 \\ 4 & 8 & 2 \end{pmatrix}$$
$$ = \begin{pmatrix} 0.5\times9 & 0.5\times6 & 0.5\times3 \\ 0.5\times5 & 0.5\times7 & 0.5\times1 \\ 0.5\times4 & 0.5\times8 & 0.5\times2 \end{pmatrix}$$
$$ = \begin{pmatrix} 4.5 & 3 & 1.5 \\ 2.5 & 3.5 & 0.5 \\ 2 & 4 & 1 \end{pmatrix}$$
EXAMPLE 7
Multiply the matrix G by the scalar $latex s=2$ and then add the matrix H:
$$G = \begin{pmatrix} 2 & 7 & 4 \\ 3 & 1 & 5 \\ 6 & 2 & 9 \end{pmatrix}$$
$$H = \begin{pmatrix} 1 & 3 & 2 \\ 0 & 1 & 4 \\ 3 & 0 & 2 \end{pmatrix}$$
Solution
First, we multiply the matrix G by the scalar $latex s=2$:
$$2 \times \begin{pmatrix} 2 & 7 & 4 \\ 3 & 1 & 5 \\ 6 & 2 & 9 \end{pmatrix}$$
$$ = \begin{pmatrix} 2\times2 & 2\times7 & 2\times4 \\ 2\times3 & 2\times1 & 2\times5 \\ 2\times6 & 2\times2 & 2\times9 \end{pmatrix}$$
$$ = \begin{pmatrix} 4 & 14 & 8 \\ 6 & 2 & 10 \\ 12 & 4 & 18 \end{pmatrix}$$
Now we add the resulting matrix to the matrix $latex H$:
$$\begin{pmatrix} 4 & 14 & 8 \\ 6 & 2 & 10 \\ 12 & 4 & 18 \end{pmatrix} + \begin{pmatrix} 1 & 3 & 2 \\ 0 & 1 & 4 \\ 3 & 0 & 2 \end{pmatrix}$$
$$ = \begin{pmatrix} 4+1 & 14+3 & 8+2 \\ 6+0 & 2+1 & 10+4 \\ 12+3 & 4+0 & 18+2 \end{pmatrix}$$
$$ = \begin{pmatrix} 5 & 17 & 10 \\ 6 & 3 & 14 \\ 15 & 4 & 20 \end{pmatrix}$$
EXAMPLE 8
Find the result of the subtraction $latex I-J$ and then multiply the resulting matrix by the scalar $latex t=-1$:
$$I = \begin{pmatrix} 5 & 8 & 3 \\ 1 & 6 & 2 \\ 7 & 3 & 1 \end{pmatrix}$$
$$ J = \begin{pmatrix} 2 & 4 & 1 \\ 1 & 2 & 0 \\ 3 & 1 & 1 \end{pmatrix}$$
Solution
Subtracting the matrix $latex J$ from the matrix $latex I$, we have:
$$\begin{pmatrix} 5 & 8 & 3 \\ 1 & 6 & 2 \\ 7 & 3 & 1 \end{pmatrix} – \begin{pmatrix} 2 & 4 & 1 \\ 1 & 2 & 0 \\ 3 & 1 & 1 \end{pmatrix}$$
$$ = \begin{pmatrix} 5-2 & 8-4 & 3-1 \\ 1-1 & 6-2 & 2-0 \\ 7-3 & 3-1 & 1-1 \end{pmatrix}$$
$$ = \begin{pmatrix} 3 & 4 & 2 \\ 0 & 4 & 2 \\ 4 & 2 & 0 \end{pmatrix}$$
Now, we multiply the resulting matrix by the scalar $latex t=-1$:
$$-1 \times \begin{pmatrix} 3 & 4 & 2 \\ 0 & 4 & 2 \\ 4 & 2 & 0 \end{pmatrix}$$
$$ = \begin{pmatrix} -1\times3 & -1\times4 & -1\times2 \\ -1\times0 & -1\times4 & -1\times2 \\ -1\times4 & -1\times2 & -1\times0 \end{pmatrix}$$
$$ = \begin{pmatrix} -3 & -4 & -2 \\ 0 & -4 & -2 \\ -4 & -2 & 0 \end{pmatrix}$$
Multiplying 2×2 matrices by a scalar – Practice problems
Write the answer in the input box.
See also
Interested in learning more about matrices? You can look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
