2×3 matrices are matrices with two rows and three columns. On the other hand, 3×2 matrices are matrices with three rows and two columns. To multiply these matrices, we multiply the elements of the rows of the first matrix by the elements of the columns of the second matrix.
Here, we will look at the steps we can follow to multiply 2×3 by 3×2 matrices. We will look at several examples with answers and practice problems to apply these concepts.
LINEAR ALGEBRA
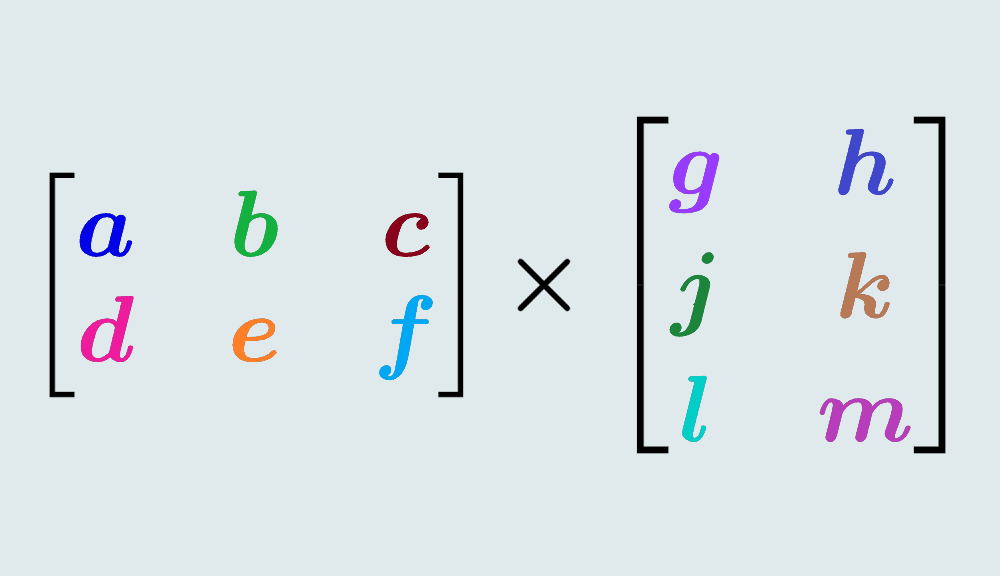
Relevant for…
Learning about 2×3 and 3×2 matrix multiplication with examples.
LINEAR ALGEBRA
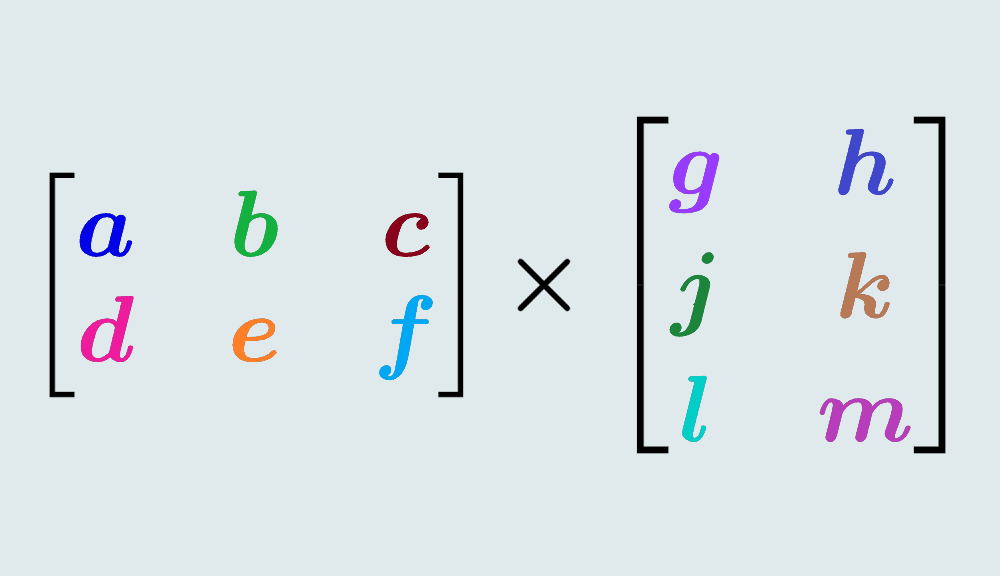
Relevant for…
Learning about 2×3 and 3×2 matrix multiplication with examples.
How to multiply 2×3 matrices by 3×2 matrices?
To multiply a 2×3 matrix by a 3×2 matrix, the number of columns of the first matrix (3) must match the number of rows of the second matrix (3).
The resulting matrix will have the same number of rows as the first matrix (2) and the same number of columns as the second matrix (2).
Suppose we have matrix A, 2×3, and matrix B, 3×2:
$$A= \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \end{pmatrix}$$
$$B=\begin{pmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \\ b_{31} & b_{32} \end{pmatrix}$$
To multiply this type of matrices and find the matrix C, we can follow the following steps:
Step 1: Multiply the first row of matrix A by the first column of matrix B to find the element $latex c_{11}$:
$$c_{11}=a_{11}b_{11} + a_{12}b_{21} + a_{13}b_{31}$$
Step 2: Multiply the first row of matrix A by the second column of matrix B to find the element $latex c_{12}$:
$$c_{11}=a_{11}b_{12} + a_{12}b_{22} + a_{13}b_{32}$$
Step 3: Repeat steps 1 and 2 for the second row of matrix A and we have:
$$C = \begin{bmatrix} a_{11}b_{11} + a_{12}b_{21} + a_{13}b_{31} & a_{11}b_{12} + a_{12}b_{22} + a_{13}b_{32}\\ a_{21}b_{11} + a_{22}b_{21} + a_{23}b_{31} & a_{21}b_{12} + a_{22}b_{22} + a_{23}b_{32} \end{bmatrix}$$
The resulting matrix is the product of the two 3×3 matrices.
$$\begin{pmatrix} c_{11} & c_{12} \\ c_{21} & c_{22}\end{pmatrix}$$
Note: Matrix multiplication is not commutative, which means that the order of the matrices matters. That is, AxB is not necessarily the same as BxA.
Solved exercises on multiplication of 2×3 and 3×2 matrices
EXAMPLE 1
Multiply matrices A and B to find the product M:
$$A=\begin{bmatrix} 1 & 2 & 3\\4 & 5 & 6 \end{bmatrix}$$
$$B=\begin{bmatrix} 7 & 8\\9 & 10\\11 & 12\end{bmatrix}$$
Solution
We find the $latex m_{11}$ term of the matrix M by multiplying the elements of the first row of the matrix A by the elements of the first column of the matrix B. Then, we have:
$latex m_{11}=(1)(7) + (2)(9) + (3)(11)$
$latex m_{11}=7 + 18+33=58$
The term $latex m_{12}$ is found by multiplying the elements of the first row of matrix A by the elements of the second column of matrix B:
$latex m_{12}=(1)(8) + (2)(10) + (3)(12)$
$latex m_{12}=8+20+36=64$
To find the term $latex m_{21}$, we take the second row of matrix A and the first column of matrix B:
$latex m_{21}=(4)(7) + (5)(9) + (6)(11)$
$latex m_{21}=28 + 45+ 66=139$
For the $latex m_{22}$ term, multiply the elements of the second row of matrix A by the corresponding elements of the second column of matrix B:
$latex m_{22}=(4)(8) + (5)(10) + (6)(12)$
$latex m_{22}=32 + 50+ 72=154$
Then, we have:
$$M=\begin{bmatrix} 58 & 64 \\ 139 & 154 \end{bmatrix}$$
EXAMPLE 2
Find the matrix M resulting from the multiplication AxB:
$$A=\begin{bmatrix} 3&4&-2\\4&2&-2 \end{bmatrix}$$
$$B=\begin{bmatrix} 4&2\\-2&1\\1&2 \end{bmatrix}$$
Solution
Multiplying the elements of each row of the first matrix by the corresponding elements of each column of the second matrix, we have:
$$M=\begin{bmatrix} (3)(4) + (4)(-2) + (-2)(1) & (3)(2) + (4)(1) + (-2)(2)\\ (4)(4) + (2)(-2) + (-2)(1) & (4)(2) + (2)(1) + (-2)(2) \end{bmatrix}$$
$$M=\begin{bmatrix}2& 6\\10& 6 \end{bmatrix}$$
EXAMPLE 3
Find the product of the multiplication A×B:
$$A=\begin{bmatrix} 4&2&-3\\5&4&3 \end{bmatrix}$$
$$B=\begin{bmatrix} -3&-5\\-3&2\\3&2 \end{bmatrix}$$
Solution
To find the elements of the product, multiply the elements of matrices A and B as follows:
$$M=\begin{bmatrix} (4)(-3) + (2)(-3) + (-3)(3) & (4)(-5) + (2)(2) + (-3)(2)\\ (5)(-3) + (4)(-3) + (3)(3) & (5)(-5) + (4)(2) + (3)(2) \end{bmatrix}$$
When solving these operations, we have:
$$M=\begin{bmatrix} -27& -22\\-18& -11 \end{bmatrix}$$
EXAMPLE 4
Solve the multiplication A×B.
$$A=\begin{bmatrix} 1&2&1\\0&8&7 \end{bmatrix}$$
$$B=\begin{bmatrix} 10&5\\-13&-5\\2&1 \end{bmatrix}$$
Solution
By multiplying the rows of the first matrix by the columns of the next matrix, we have the following:
$$M=\begin{bmatrix} (1)(10) + (2)(-13) + (1)(2) & (1)(5) + (2)(-5) + (1)(1)\\ (0)(10) + (8)(-13) + (7)(2) & (0)(5) + (8)(-5) + (7)(1) \end{bmatrix}$$
When simplifying, we have:
$$M=\begin{bmatrix} -14& -4\\-90& -33 \end{bmatrix}$$
EXAMPLE 5
What is the result of multiplying A×B?
$$A=\begin{bmatrix} -3&-4&3\\4&2&8 \end{bmatrix}$$
$$B=\begin{bmatrix} 9& 2\\-3&-4\\5&4 \end{bmatrix}$$
Solution
Create a matrix as follows:
$$M=\begin{bmatrix} (-3)(9) + (-4)(-3) + (3)(5) & (-3)(2) + (-4)(-4) + (3)(4)\\ (4)(9) + (2)(-3) + (8)(5) & (4)(2) + (2)(-4) + (8)(4) \end{bmatrix}$$
Simplifying, we have:
$$M=\begin{bmatrix} 0& 22\\70& 32 \end{bmatrix}$$
EXAMPLE 6
Find the result of the multiplication A×B:
$$A=\begin{bmatrix} -6&-7&1\\-2&4&7 \end{bmatrix}$$
$$B=\begin{bmatrix} 7& 5\\-5&-2\\6&4 \end{bmatrix}$$
Solution
Multiply the elements of each row of the first matrix by the corresponding elements of the columns of the second matrix:
$$M=\begin{bmatrix}(-6)(7) + (-7)(-5) + (1)(6) & (-6)(5) + (-7)(-2) + (1)(4) \\ (-2)(7) + (4)(-5) + (7)(6) & (-2)(5) + (4)(-2) + (7)(4) \end{bmatrix} $$
When solving this, we have:
$$M=\begin{bmatrix} -1& -12\\8& 10 \end{bmatrix}$$
EXAMPLE 7
Solve the multiplication A×B:
$$A=\begin{bmatrix} -4&-5&6\\-3&5&8 \end{bmatrix}$$
$$B=\begin{bmatrix} 5& 6\\-3&-4\\2&5 \end{bmatrix}$$
Solution
Form the following matrix:
$$M=\begin{bmatrix} (-4)(5) + (-5)(-3) + (6)(2) & (-4)(6) + (-5)(-4) + (6)(5) \\ (-3)(5) + (5)(-3) + (8)(2) & (-3)(6) + (5)(-4) + (8)(5) \end{bmatrix} $$
Simplifying, we have:
$$M=\begin{bmatrix} 7& 26\\-14& 2 \end{bmatrix}$$
Multiplication of 2×3 and 3×2 matrices – Practice problems
Write the answer in the input box.
See also
Interested in learning more about matrices? You can take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
