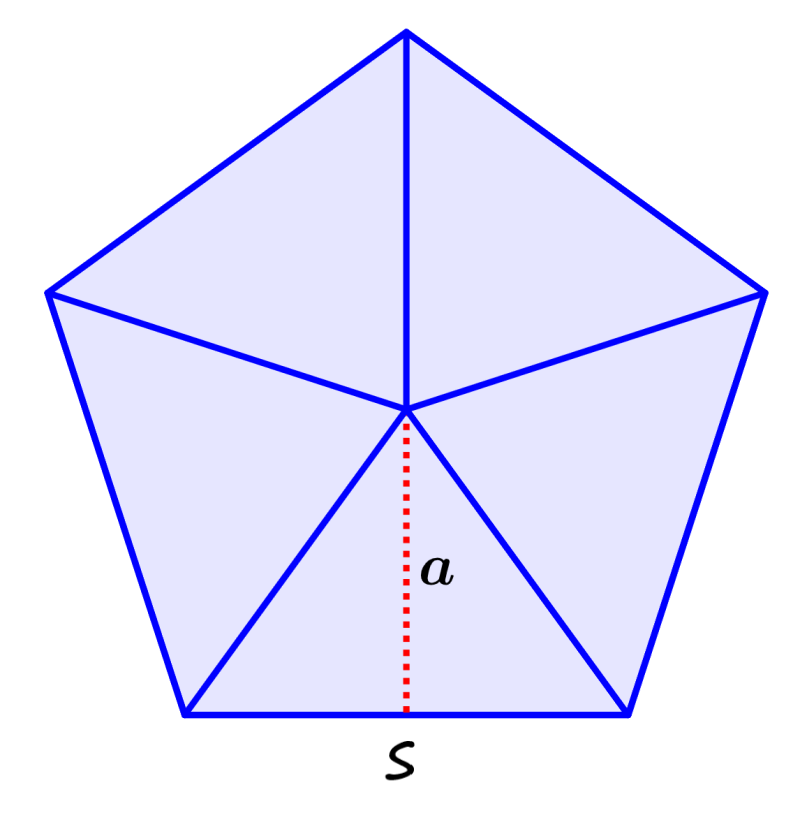
The pentagon is a geometric figure that has five sides and five angles. The interior angles in a pentagon add up to 540°. Depending on the characteristics that we take, we can distinguish some types of pentagons. We can have regular and irregular pentagons and convex and concave pentagons.
Here, we will look at a definition of pentagons and a brief description of the types of pentagons. Also, we will learn about some of the most important characteristics of these geometric figures. In addition, we will review its most important formulas and apply them to solve some regular pentagons problems.
Definition of a pentagon
A pentagon is a polygon with 5 sides and 5 angles. The word “pentagon” is made up of two parts, penta and gonia, which mean five angles. All the sides of the pentagon meet each other end to end to form a shape. Depending on the sides, angles, and vertices, there are different types of pentagons such as:
- Regular and irregular
- Convex and concave
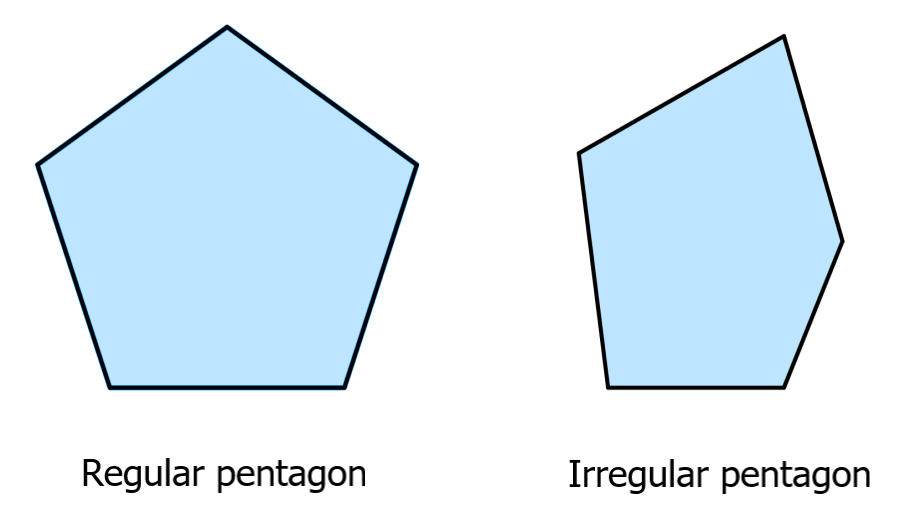
Irregular and regular pentagons
If a pentagon is regular, all the sides have the same lengths and all five angles have the same measure. If the pentagon has no sides with equal lengths or angles with the same measure, then it is an irregular pentagon.
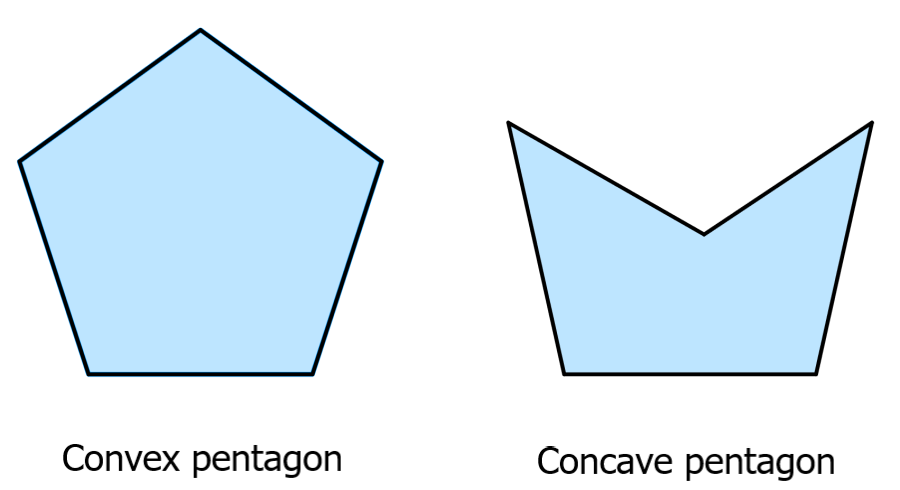
Convex and concave pentagons
If all the vertices of a pentagon are pointing outward, the pentagon is convex. On the other hand, if the pentagon has at least one vertex that is pointing inward, then the pentagon is concave.
Fundamental characteristics of a pentagon
The following are some of the most important characteristics of a pentagon:
- The sum of all the interior angles is 540°.
- A regular polygon has all five sides with the same length.
- A regular polygon has all five angles with the same measure.
- In a regular polygon, each interior angle measures 108° and each exterior angle measures 72°.
Important pentagon formulas
The most important formulas for pentagons are the perimeter formula, the area formula, and the apothem formula.
Formula for the perimeter of a pentagon
Since all sides of the regular pentagon have the same length, the perimeter of a pentagon is:
| $latex p=5s$ |
where s is the length of the sides of the pentagon.
Formula for the area of a pentagon
For a regular pentagon, the area is given by:
| $latex A= \frac{5}{2} sa$ |
where s is the length of one of the sides and a is the length of the apothem.
Formula of the apothem of a pentagon
A regular pentagon has the following apothem:
| $latex a=\frac{s}{2 \tan (36)}$ |
where s is the length of one side of the pentagon.
Examples of pentagon problems
EXAMPLE 1
- What is the perimeter of a pentagon that has sides of length 23 m?
Solution: We use the perimeter formula with $latex s=23$:
$latex p=5s$
$latex p=5(23)$
$latex p=115$
The perimeter is 115 m.
EXAMPLE 2
- What is the area of a pentagon that has sides of length 10 m and an apothem of length 6.88 m?
Solution: We use the area formula with $latex s=10$ and $latex a=6.88$:
$latex A= \frac{5}{2}sa$
$latex A= \frac{5}{2}(10)(6.88)$
$latex A=172$
The area of the pentagon is 172 m².
EXAMPLE 3
- What is the apothem of a pentagon that has sides of length 8m?
Solution: We use the apothem formula with $latex s=8$:
$latex a= \frac{s}{2\tan(36°)}$
$latex a= \frac{8}{2\tan(36°)}$
$latex a= \frac{8}{1.453}$
$latex a=5.5$
The length of the apothem is 5.5 m.
Pentagon – Practice problems
See also
Interested in learning more about pentagons? Take a look at these pages: