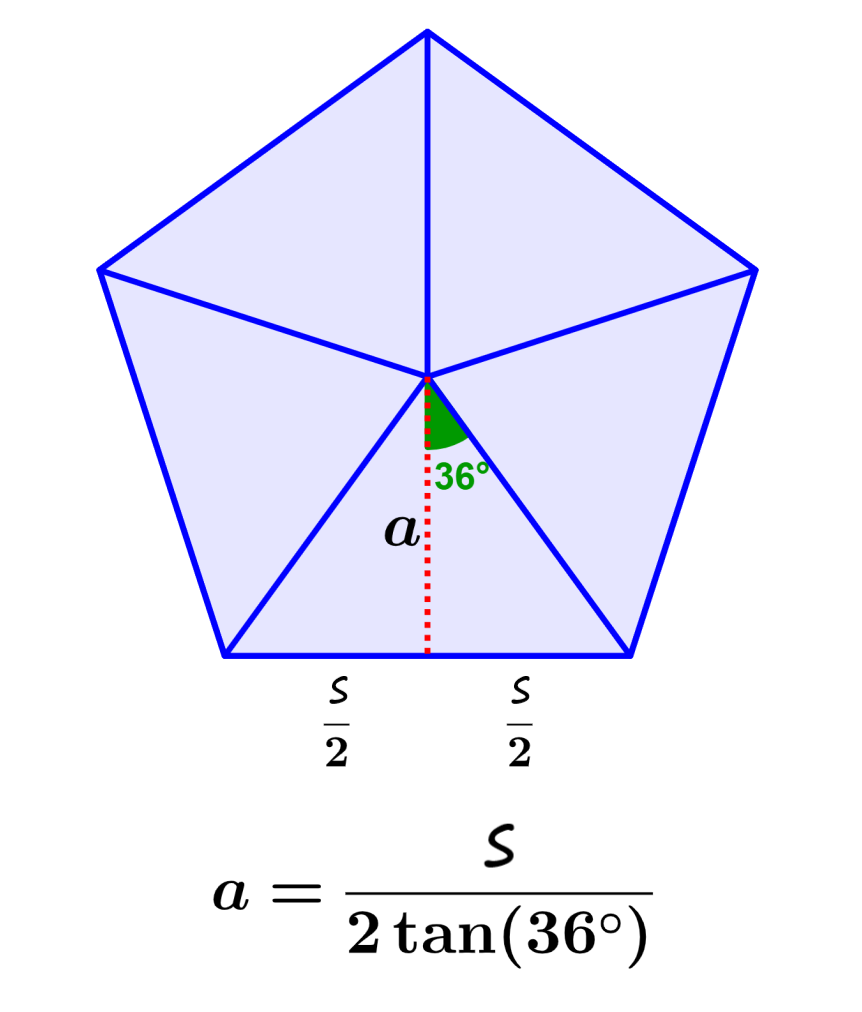
The apothem of a pentagon is the perpendicular distance from the center of the pentagon to the center of one of its sides. The apothem can also be considered as the radius of the incircle of a polygon. The apothem is used mainly to calculate the area of a regular polygon.
Here, we will learn how to calculate the apothem of a pentagon. In addition, we will use the apothem formula to solve some examples.
Formula to find the apothem of a pentagon
To find the formula for the apothem, we can use the diagram of a pentagon:
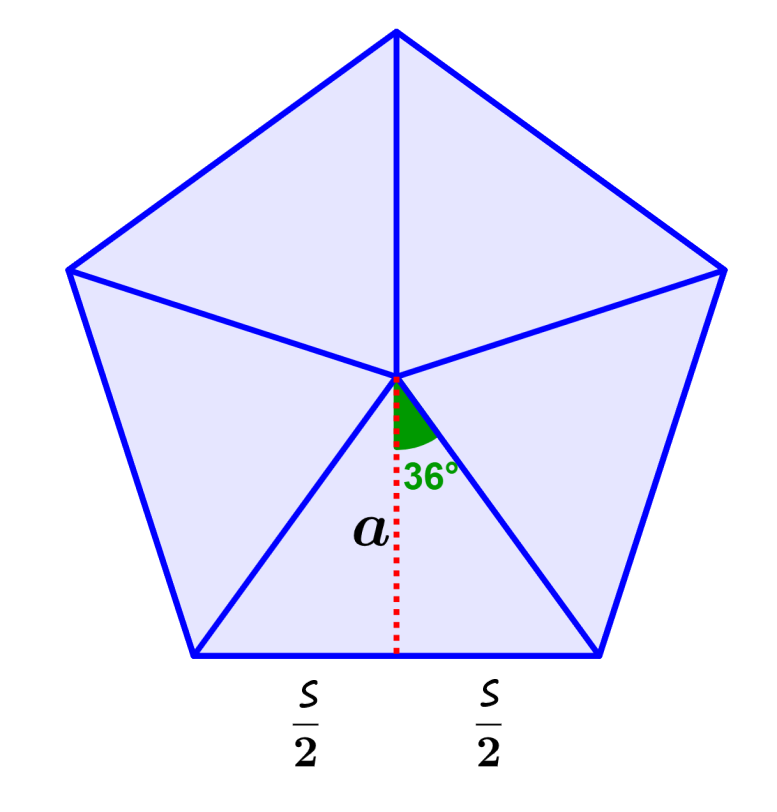
Here, we divide the pentagon into five congruent triangles and use one of the triangles to find the apothem. We can see that the apothem is the height of one of the triangles and divides one of the sides into two equal parts.
We can use trigonometry to find the length of the apothem. We start by finding the angle of the center of the apothem. We have five triangles and by dividing each triangle in two, we would have 10 small triangles.
Also, we know that a complete circle has 360°, so when dividing by the 10 triangles, we have 36°. The angle at the center of the pentagon always measures 36°.
We use the tangent to calculate the height of the triangle. In a right triangle, the tangent of an angle is equal to the length of the opposite side divided by the length of the adjacent side.
The side opposite the 36° angle is the base of the triangle (half the length of one side of the pentagon). The side adjacent to the 36° angle is the height of the triangle. Therefore, we have:
$latex \tan(36°)= \frac{ \text{opposite}}{ \text{adjacent}}$
$latex \tan(36°)= \frac{ \frac{s}{2}}{a}$
$latex \tan(36°)= \frac{s}{2a}$
$latex a= \frac{s}{2\tan(36°)}$
where, a represents the length of the apothem and s represents the length of one of the sides of the pentagon.
Apothem of a pentagon – Examples with answers
The formula for the apothem of a pentagon is used to solve the following examples. Each example has its respective solution, but it is recommended that you try to solve the problems yourself before looking at the answer.
EXAMPLE 1
What is the length of the apothem of a pentagon that has sides of length 4 m?
Solution
We use the apothem formula with $latex s=4$. Therefore, we have:
$latex a= \frac{s}{2 \tan(36°)}$
$latex a= \frac{4}{2 \tan(36°)}$
$latex a= \frac{4}{1.453}$
$latex a=2.75$
The length of the apothem is 2.75 m.
EXAMPLE 2
The length of the sides of a pentagon is 5 m. What is the length of the apothem?
Solution
We have that the sides have a length of $latex s = 5$. Therefore, using this value in the formula, we have:
$latex a= \frac{s}{2 \tan(36°)}$
$latex a= \frac{5}{2 \tan(36°)}$
$latex a= \frac{5}{1.453}$
$latex a=3.44$
The length of the apothem is 3.44 m.
EXAMPLE 3
A pentagon has sides that are 10 m long. What is the length of its apothem?
Solution
Here, the length of the pentagon’s sides is $latex s=10$. Therefore, substituting this value in the formula, we have:
$latex a= \frac{s}{2 \tan(36°)}$
$latex a= \frac{10}{2 \tan(36°)}$
$latex a= \frac{10}{1.453}$
$latex a=6.88$
The length of the apothem is 6.88 m.
EXAMPLE 4
A pentagon has an apothem of length 7.6 m. What is the length of its sides?
Solution
In this case, we start with the length of the apothem and we want to know the length of the sides of the pentagon. Therefore, we use the formula with $latex a=7.6$ and solve for s:
$latex a= \frac{s}{2 \tan(36°)}$
$latex 7.6= \frac{s}{2 \tan(36°)}$
$latex 7.6= \frac{s}{1.453}$
$latex s= (7.6)(1.453)$
$latex s=11.04$
The length of the sides is 11.04 m.
EXAMPLE 5
What is the length of the sides of a pentagon that has an apothem with a length of 6 m?
Solution
Again, we start with the length of the apothem and we are going to find the length of the sides of the pentagon. Therefore, we use the value $latex a=6$ in the formula and solve for s:
$latex a= \frac{s}{2 \tan(36°)}$
$latex 6= \frac{s}{2 \tan(36°)}$
$latex 6= \frac{s}{1.453}$
$latex s= (6)(1.453)$
$latex s=8.72$
The length of the sides is 8.72 m.
Apothem of a pentagon – Practice problems
Put into practice the use of the pentagons apothem formula to solve the following problems. If you need help, you can look at the solved examples above.
See also
Interested in learning more about pentagons? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
