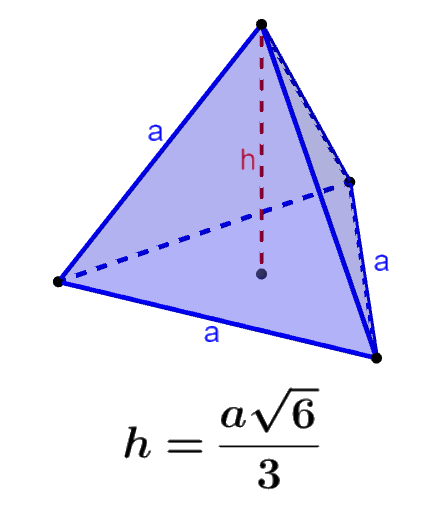
The regular tetrahedron is one of the five Platonic solids. We can think of a tetrahedron as a regular triangular pyramid. Its height can be calculated using a formula derived using the Pythagorean theorem.
Here, we will learn about the formula for the height of a regular tetrahedron. We will learn how to derive this formula, and we will apply it to solve some practice problems.
GEOMETRY
Relevant for…
Learning to calculate the height of a tetrahedron with examples.
GEOMETRY
Relevant for…
Learning to calculate the height of a tetrahedron with examples.
Formula for the height of a tetrahedron
Tetrahedra are three-dimensional figures that have all their faces with a triangular shape. Tetrahedra can be considered as regular triangular pyramids.
The height of a tetrahedron is the length of the segment perpendicular to the base and connecting to the opposite vertex. The formula for the height of a regular tetrahedron is:
| $latex h=\frac{a\sqrt{6}}{3}$ |
Proof of the formula for the height of a tetrahedron
To derive the formula for the height of a tetrahedron, we consider the following figure:
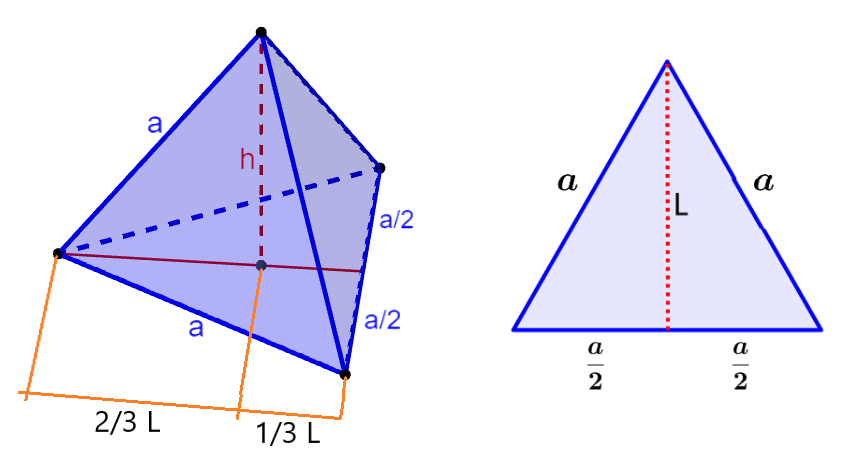
We can see that the height is the segment perpendicular to the base of the tetrahedron that joins its base with the opposite vertex. From the diagram, we can see that the height starts from 2/3 of L, where L is the height of one face of the tetrahedron.
We can calculate the length of the height of the tetrahedron using the Pythagorean theorem, where a is the hypotenuse, h is one leg, and 2/3 of L is the other leg. Therefore, we have
$latex {{h}^2}+{{(\frac{2}{3}L)}^2}={{a}^2}$
$latex {{h}^2}+\frac{4}{9}{{L}^2}={{a}^2}$
Now, considering that the faces of a regular tetrahedron are equilateral triangles, we can find an expression for L, remembering that the height of an equilateral triangle is equal to $latex \frac{a~\sqrt{3}}{2}$.
Substituting this into the equation, we have:
$latex {{h}^2}+\frac{4}{9}{{(\frac{a~\sqrt{3}}{2})}^2}={{a}^2}$
$latex {{h}^2}+\frac{4}{9}(\frac{{{a}^2}(3)}{4})={{a}^2}$
$latex {{h}^2}+\frac{{{a}^2}}{3}={{a}^2}$
$latex {{h}^2}={{a}^2}-\frac{{{a}^2}}{3}$
$latex {{h}^2}=\frac{2{{a}^2}}{3}$
$latex h=\frac{\sqrt{2{{a}^2}}}{\sqrt{3}}$
$latex h=\frac{a~\sqrt{2}}{\sqrt{3}}$
$latex h=\frac{a~\sqrt{2}(\sqrt{3})}{3}$
$latex h=\frac{a~\sqrt{6})}{3}$
Height of a tetrahedron – Examples with answers
The formula for the height of a tetrahedron is used to solve the following examples. Try to solve the problems yourself before looking at the answer.
EXAMPLE 1
If the sides of a tetrahedron are 4 m long, what is its height?
Solution
We have to use the height formula with the value a=4. Therefore, we have:
$latex h=\frac{a~\sqrt{6}}{3}$
$latex h=\frac{4~\sqrt{6}}{3}$
$latex h=3.27$
The height of the tetrahedron is 3.27 m.
EXAMPLE 2
Determine the height of a tetrahedron that has sides with a length of 6 m.
Solution
Using the value a=6 in the formula for the height of the tetrahedron, we have:
$latex h=\frac{a~\sqrt{6}}{3}$
$latex h=\frac{6~\sqrt{6}}{3}$
$latex h=4.9$
Therefore, the height of the tetrahedron is 4.9 m.
EXAMPLE 3
What is the height of a tetrahedron that has sides with a length of 10 cm?
Solution
We are going to apply the formula for the height of a tetrahedron using the value a=10. Therefore, we have
$latex h=\frac{a~\sqrt{6}}{3}$
$latex h=\frac{10~\sqrt{6}}{3}$
$latex h=8.16$
Then, the height of the tetrahedron is 8.16 cm.
EXAMPLE 4
If a tetrahedron has a height of 8 m, what is the length of one of its sides?
Solution
In this case, we know the length of the height, and we have to calculate the length of one of the sides. Therefore, we have to use the height formula and solve for a:
$latex h=\frac{a~\sqrt{6}}{3}$
$latex 8=\frac{a~\sqrt{6}}{3}$
$latex 24=a~\sqrt{6}$
$latex a=9.8$
So the sides of the tetrahedron are 9.8 m long.
EXAMPLE 5
A tetrahedron has a height with a length of 15 cm. Determine the length of its sides.
Solution
Similar to the previous problem, we are going to use the height formula to then solve for a:
$latex h=\frac{a~\sqrt{6}}{3}$
$latex 15=\frac{a~\sqrt{6}}{3}$
$latex 45=a~\sqrt{6}$
$latex a=18.37$
The sides of the tetrahedron have a length of 18.37 m.
EXAMPLE 6
What is the height of a tetrahedron that has sides with a length of 11.5 cm?
Solution
By applying the height formula with the value a=11.5, we have:
$latex h=\frac{a~\sqrt{6}}{3}$
$latex h=\frac{11.5~\sqrt{6}}{3}$
$latex h=9.4$
Therefore, the height of the tetrahedron is 9.4 cm.
EXAMPLE 7
Determine the height of a tetrahedron that has side lengths of 24.5 m.
Solution
Using the value a=24.5 in the formula for the height of the tetrahedron, we have:
$latex h=\frac{a~\sqrt{6}}{3}$
$latex h=\frac{24.5~\sqrt{6}}{3}$
$latex h=20$
The height of the tetrahedron is 20 m.
Height of a tetrahedron – Practice problems
Use what you have learned about the height of a tetrahedron to solve the following exercises. If you have problems with these exercises, you can guide yourself with the examples solved above.
See also
Interested in learning more about tetrahedra? Look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
