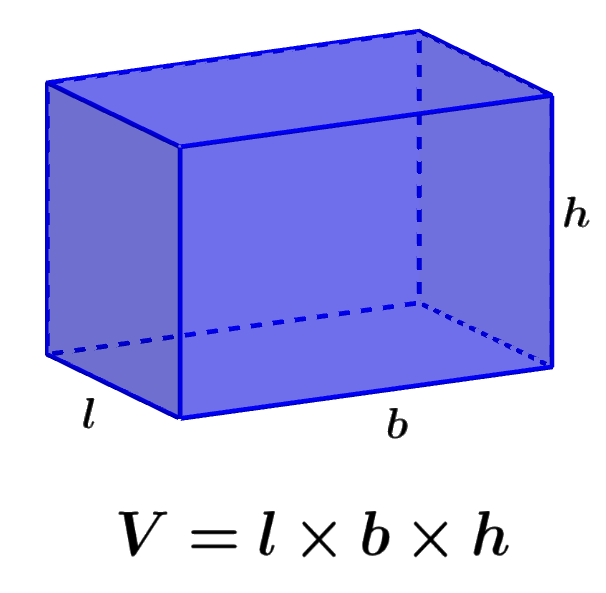
The volume of a rectangular prism is the measure of the space occupied by the prism. A rectangular prism is a three-dimensional object with six rectangular faces. A rectangular prism is also known as a cuboid, a rectangular hexahedron, or a rectangular parallelepiped. To find the volume of a rectangular prism, we multiply the dimensions of the length, width, and height.
Here, we will learn about the formula used to calculate the volume of these geometric figures. In addition, we will solve some exercises in which we will apply this formula to obtain the answer.
Formula to find the volume of a rectangular prism
The formula for the volume of a rectangular prism is obtained by multiplying the length, width, and height of the prism. Recall that a rectangular prism has two parallel rectangular bases and four rectangular faces. All the angles in these prisms are right angles.
The formula for the volume of a rectangular prism is:
| $latex V=l\times b \times h$ |
where,
- l is the length of the width of the prism
- b is the length of the base
- h is the length of the height of the prism
Volume of a rectangular prism – Examples with answers
The formula for the volume of rectangular prisms is used to solve the following examples. Try to solve the problems yourself before looking at the solution.
EXAMPLE 1
A rectangular prism has a base of 5 m, a width of 4 m, and a height of 4 m. What is its volume?
Solution
We have the dimensions:
- Base, $latex b=5$
- Width, $latex l=4$
- Height, $latex h=4$
Using the volume formula with these values, we have:
$latex V=b \times l \times h$
$latex V=5 \times 4 \times 4$
$latex V=80$
The volume is equal to 80 m³.
EXAMPLE 2
If a prism has a base of 8 m, a width of 6 m, and a height of 7 m, what is its volume?
Solution
We have the following values:
- Base, $latex b=8$
- Width, $latex l=6$
- Height, $latex h=7$
Substituting these values in the volume formula, we have:
$latex V=b \times l \times h$
$latex V=8 \times 6 \times 7$
$latex V=336$
The volume is equal to 336 m³.
EXAMPLE 3
A rectangular prism has a base of 10 m, a width of 11 m, and a height of 12 m. What is its volume?
Solution
We recognize the following values:
- Base, $latex b=10$
- Width, $latex l=11$
- Height, $latex h=12$
Using these values in the formula, we have:
$latex V=b \times l \times h$
$latex V=10 \times 11 \times 12$
$latex V=1320$
The volume is equal to 1320 m³.
EXAMPLE 4
What is the length of the height of a prism that has a base of 5 m, a width of 3 m, and a volume of 90 m³?
Solution
We have the values:
- Base, $latex b=5$
- Width, $latex l=3$
- Volume, $latex V=90$
In this case, we have the volume and we want to find the length of the height. Therefore, we have to use the volume formula and solve for h:
$latex V=b \times l \times h$
$latex 90=5 \times 3 \times h$
$latex 90=15h$
$latex h=6$
The length of the height is 6 m.
EXAMPLE 5
A rectangular prism has a volume of 693 m³, a base of 11 m, and a width of 9 m. What is its height?
Solution
We have the values:
- Base, $latex b=11$
- Width, $latex l=9$
- Volume, $latex V=693$
We use the volume formula and solve for h:
$latex V=b \times l \times h$
$latex 693=11 \times 9 \times h$
$latex 693=99h$
$latex h=7$
The length of the height is 7 m.
Volume of a rectangular prism – Practice problems
Use the formula for the volume of rectangular prisms to solve the following problems. If you need help with this, you can look at the solved examples above.
See also
Interested in learning more about rectangular prisms? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
