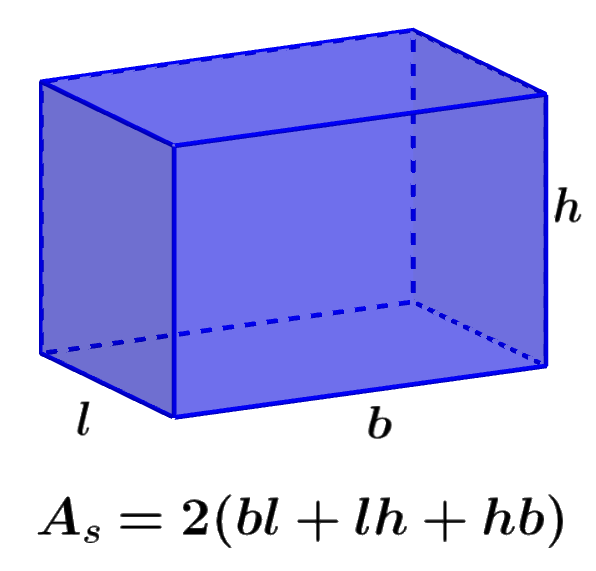
The surface area of a rectangular prism is equal to the total area occupied by the prism. The surface area is a two-dimensional measurement, so it can be measured in m², cm², among others. To calculate the surface area, we have to add the individual areas of all the faces of the rectangular prism. In total, we have 6 faces in a rectangular prism, so we add the areas of the six faces. The area of each face depends on two of the three dimensions of the prism, length, base, and height.
Here, we will learn about the formula that we can use to find the surface area of rectangular prisms. In addition, we will solve some problems, in which we will apply this formula.
Formula to find the surface area of a rectangular prism
A rectangular prism has two parallel rectangular bases and four rectangular faces. The surface area of the rectangular prism is the sum of the area of the lateral faces and the rectangular bases. The unit of measurement of the surface area of the rectangular prism is square units.
Let’s consider the following rectangular prism with its dimensions:
The formula for the surface area of this rectangular prism is:
| $latex A_{S}=2(bl+lh+hb)$ |
where,
- b is the length of the base
- l is the length of the width of the prism
- h is the length of the height of the prism
This formula is derived by considering that the parallel faces in a rectangular prism have the same area.
Surface area of a rectangular prism – Examples with answers
The formula for the surface area of rectangular prisms is applied to solve the following examples. Each example has its respective solution, but it is recommended that you try to solve the problems yourself.
EXAMPLE 1
A rectangular prism has a base of 5 m, a width of 4 m, and a height of 4 m. What is its surface area?
Solution
We can obtain the following information:
- Base, $latex b=5$
- Width, $latex l=4$
- Height, $latex h=4$
We use the formula for surface area with these values. Therefore, we have:
$latex A_{S}=2(bl+lh+hb)$
$latex A_{S}=2((5)(4)+(4)(4)+(4)(5))$
$latex A_{S}=2(20+16+20)$
$latex A_{S}=2(56)$
$latex A_{S}=112$
The surface area is 112 m².
EXAMPLE 2
What is the surface area of a rectangular prism that has a base of 7 m, a width of 6 m, and a height of 8 m?
Solution
From the question, we have the following values:
- Base, $latex b=7$
- Width, $latex l=6$
- Height, $latex h=8$
We substitute these values in the formula for surface area:
$latex A_{S}=2(bl+lh+hb)$
$latex A_{S}=2((7)(6)+(6)(8)+(8)(7))$
$latex A_{S}=2(42+48+56)$
$latex A_{S}=2(146)$
$latex A_{S}=292$
The surface area is 292 m².
EXAMPLE 3
If a rectangular prism has a base of 8 m, a height of 12 m, and a width of 11 m. What is its surface area?
Solution
We have the following information:
- Base, $latex b=8$
- Width, $latex l=11$
- Height, $latex h=12$
Using these values in the formula for surface area, we have:
$latex A_{S}=2(bl+lh+hb)$
$$A_{S}=2((8)(11)+(11)(12)+(12)(8))$$
$latex A_{S}=2(88+132+96)$
$latex A_{S}=2(316)$
$latex A_{S}=632$
The surface area is 632 m².
EXAMPLE 4
What is the length of the height of a rectangular prism that has a surface area of 148 m² if its base is 6 m and its width is 4 m?
Solution
We have the following information:
- Base, $latex b=6$
- Width, $latex l=4$
- Surface area, $latex A=148$
Here, we have the surface area and we want to find the length of the height. Therefore, we use the formula and solve for h:
$latex A_{S}=2(bl+lh+hb)$
$latex 148=2((6)(4)+(4)h+(6)(h))$
$latex 148=2(24+10h)$
$latex 74=24+10h)$
$latex 10h=74-24$
$latex 10h=50$
$latex h=5$
The length of the height is 5 m.
EXAMPLE 5
What is the length of the height of a rectangular prism that has a surface area of 340 m², a width of 5 m, and a base of 8 m?
Solution
We have the following values:
- Base, $latex b=8$
- Width, $latex l=5$
- Surface area, $latex A=340$
We use the formula for surface area with these values and solve for h:
$latex A_{S}=2(bl+lh+hb)$
$latex 340=2((8)(5)+(5)h+(8)(h))$
$latex 340=2(40+13h)$
$latex 170=40+13h)$
$latex 13h=170-40$
$latex 13h=130$
$latex h=10$
The length of the height is 10 m.
Surface area of a rectangular prism – Practice problems
The following problems can be used to practice using the formula for the surface area of regular prisms. If you need help with these problems, you can look at the solved examples above.
See also
Interested in learning more about rectangular prisms? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
