The prism is a polyhedron in which two faces are equal polygons in parallel planes and all the other four faces are parallelograms. In the case of rectangular prisms, all faces have a rectangle shape. There are two main types of these prisms: right prisms and oblique prisms. An oblique prism is when the base is not perpendicular to the axis and the right prism is when the axis and the base are perpendiculars. The most common are right prisms.
Here, we will learn about the most important elements of a rectangular prism. Also, we will look at their most-used formulas and apply them to solve some prism exercises.
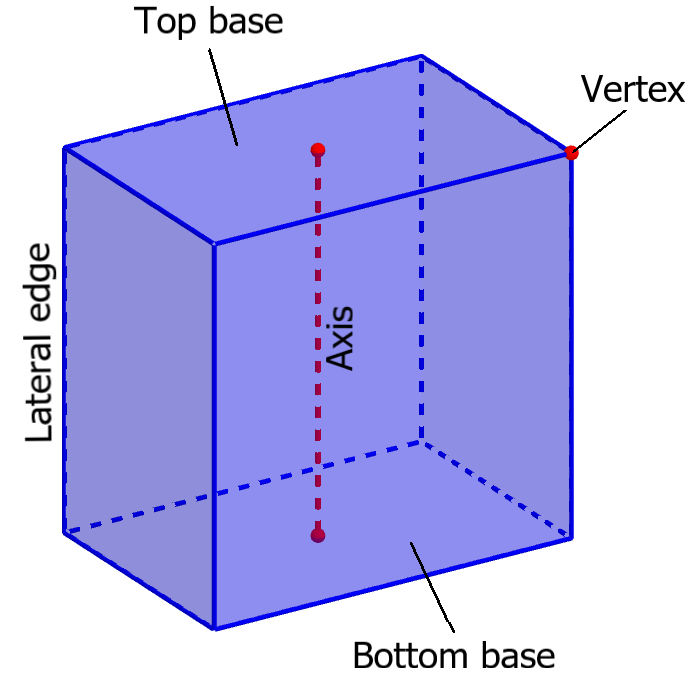
Elements of a rectangular prism
The elements of a rectangular prism are:
- Base
- Height
- Axis
- Lateral edge
- Lateral area
- Cross section
- Vertex
Base
A prism has two equal parallel bases, the top base, and the bottom base. The area of the base is denoted by $latex A_{b}$.
Height
The height is the perpendicular distance between the two bases. This length is denoted by h.
Axis
The axis is the line that connects the centroid of the lower and upper base. The length of the axis is equal to the length of the lateral edge.
Lateral edge
The lateral edges are the lines that connect to the corresponding vertices of the bases. In general, an edge is a segment formed by the intersection of two faces. The lateral edge is the line formed by the intersection of two lateral faces.
Lateral area
The lateral area is the area of the lateral faces of the prism. Opposite faces in a rectangular prism are the same, so these prisms can have two different side areas.
Cross section
The cross-section is the section formed by cutting the prism with a plane that is perpendicular to the axis of the prism.
Vertex
The vertex of a rectangular prism is a point formed by the intersection of three edges.
Important formulas of a rectangular prism
The most used formulas in rectangular prisms are the volume formula, the surface area formula, and the diagonal formula.
Formula for the volume
The volume of a rectangular prism can be calculated by multiplying the lengths of the three dimensions:
| $latex V=b\times l \times h$ |
where b is the length of the base, l is the length of the width, and h is the length of the height of the rectangular prism.
Formula for the surface area
We calculate the surface area by adding the areas of all the faces of the prism. Considering that the opposite faces have the same area, we have:
| $latex A_{s}=2(bl+bh+hl)$ |
Formula for the diagonal
The length of the diagonal of a rectangular prism is calculated using the Pythagorean theorem in three dimensions:
| $latex d=\sqrt{{{b}^2}+{{l}^2}+{{h}^2}}$ |
Examples of problems with rectangular prisms
EXAMPLE 1
If a rectangular prism has a base of length 6 m, a width of 7 m, and a height of 10 m, what is its volume?
Solution: We use the volume formula with the given information:
$latex V=b\times l \times h$
$latex V=6\times 7 \times 10$
$latex V=420$
The volume of the prism is 420 m³.
EXAMPLE 2
What is the surface area of a rectangular prism that has a base of 6 m, a width of 8 m, and a height of 7 m?
Solution: We use the formula for surface area with the given information:
$latex A_{s}=2(bl+bh+hl)$
$latex A_{s}=2((6)(8)+(6)(7)+(7)(8))$
$latex A_{s}=2(48+42+56)$
$latex A_{s}=2(146)$
$latex A_{s}=292$
The surface area of the prism is 292 m².
EXAMPLE 3
What is the diagonal of a rectangular prism that has a base of 5 m, a width of 4 m, and a height of 3 m?
Solution: We use the diagonal formula with the given information:
$latex d=\sqrt{{{b}^2}+{{l}^2}+{{h}^2}}$
$latex d=\sqrt{{{5}^2}+{{4}^2}+{{3}^2}}$
$latex d=\sqrt{25+16+9}$
$latex d=\sqrt{50}$
$latex d=7.07$
The diagonal of the prism measures 7.07 m.
See also
Interested in learning more about rectangular prisms? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
