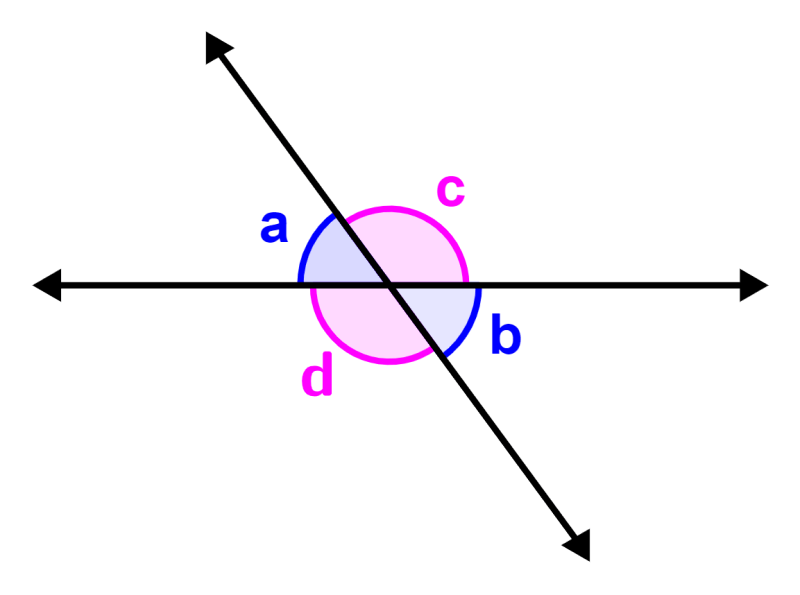
When two lines intersect each other, then the opposite angles, formed due to the intersection, are called vertical angles or vertex angles. A pair of opposite angles are always equal to each other. Also, an opposite angle and its adjacent angle are supplementary angles since they add up to 180 degrees.
In this article, we will review what it means to have intersecting lines and parallel lines. Then, we will look at the vertex angles in more detail and use diagrams to illustrate them. In addition, we will learn about the theorem of opposite angles and we will solve some exercises with these angles.
What are intersecting and parallel lines?
Intersecting lines are lines that meet or cross each other at a specific point. The following is an illustration of intersecting lines:
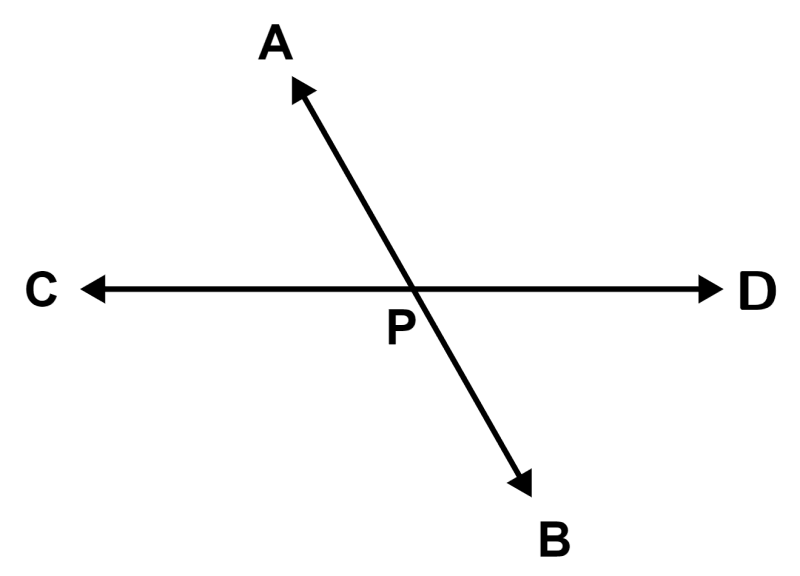
Line AB and line CD meet at point P. Therefore, the two lines are intersecting lines.
Parallel lines are lines that do not meet anywhere in the plane, as we have in the following diagram:
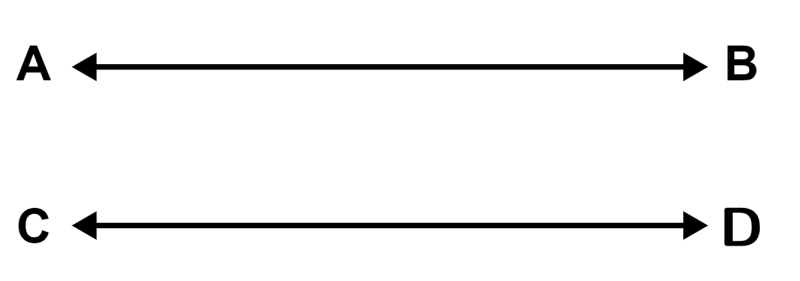
Lines AB and CD are parallel since they do not intersect at any point.
What are the opposite angles by the vertex?
Opposite angles are pairs of angles formed when two lines intersect. These angles are also called opposite vertical angles. Opposite angles are always equal to each other. In general, we can say that two pairs of opposite angles are formed when two lines intersect, as in the following diagram:
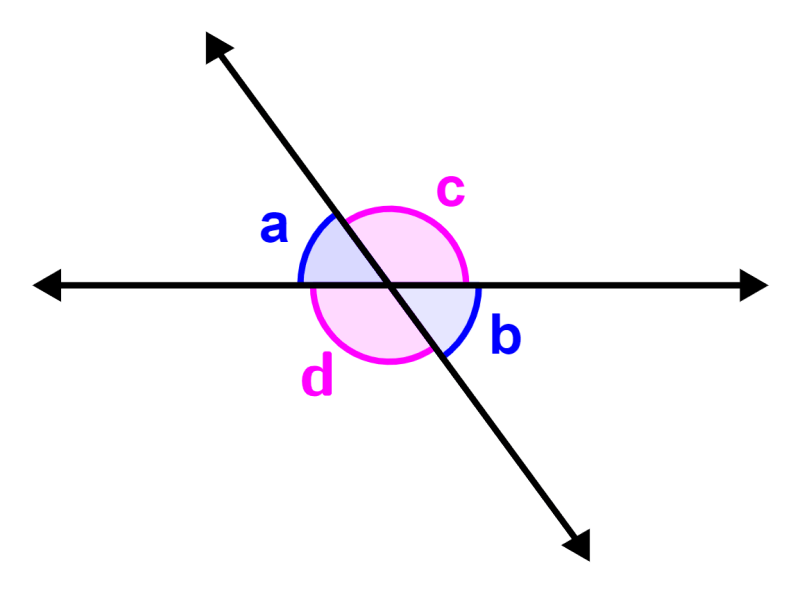
In this diagram:
- ∠a and ∠b are opposite angles. These angles are equal: ∠a = ∠b.
- ∠c and ∠d are opposite angles. These angles are equal: ∠c = ∠d.
Vertex Angles Theorem
This theorem indicates that “in a pair of intersecting lines, the angles opposed by the vertex are equal”.
Proof of the theorem: To prove this theorem, consider two lines AB and CD, which intersect at O. The two pairs of opposite angles are:
- ∠1 and ∠ 2
- ∠3 and ∠4
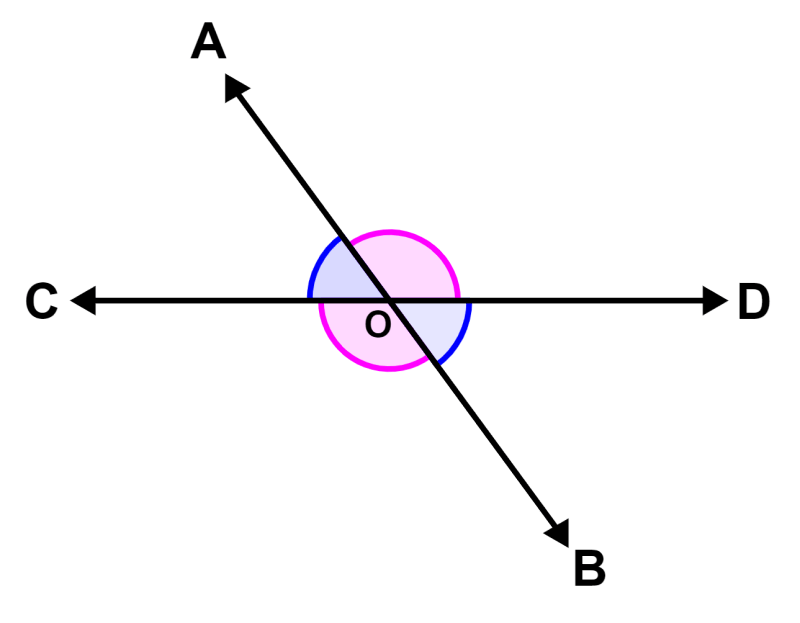
We can see that the ray OA is located on the line CD and according to the axiom of linear pairs, if a ray is located on a line, the adjacent angles form a linear pair of angles. Therefore, we have:
∠1 + ∠3 = 180° (linear pair)
In the same way, the ray OD is located on the line AB, so we also have:
∠3 + ∠2 = 180° (linear pair)
If we combine these two equations, we have:
∠1 + ∠3 = ∠3 + ∠2
∠1 = ∠2
Therefore, the pair of opposite sides are equal. We can use the same process to demonstrate this with the other pair of opposite sides.
Opposite angles by the vertex examples with answers
The properties of opposite angles can be used to solve the following exercises.
EXAMPLE 1
Calculate the missing angles in the following figure:
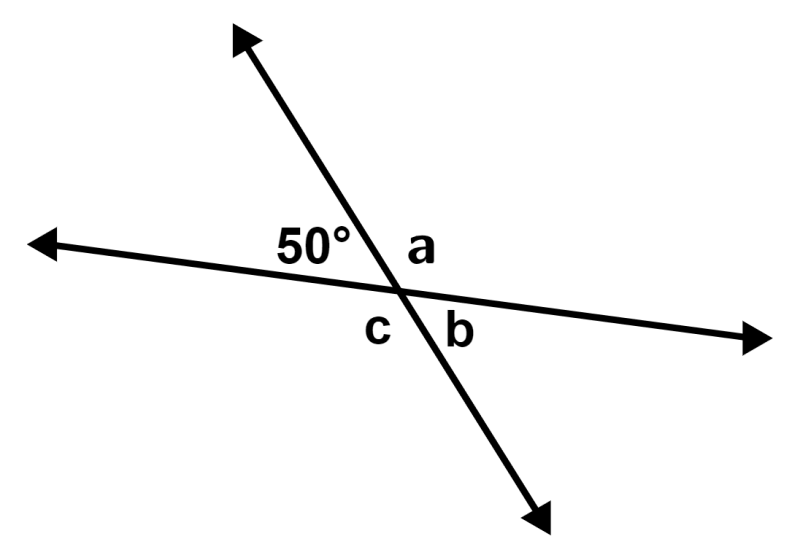
Solution: The angles ∠50° and ∠b are opposite vertical angles, so they are equal and we have:
∠b = 50°
The angles ∠50° and ∠a are supplementary angles, so we have:
50° + ∠a = 180°
∠a = 130°
The angles ∠a and ∠c are opposite, so we have:
∠c = 130°
EXAMPLE 2
Calculate the value of Y in the following figure:
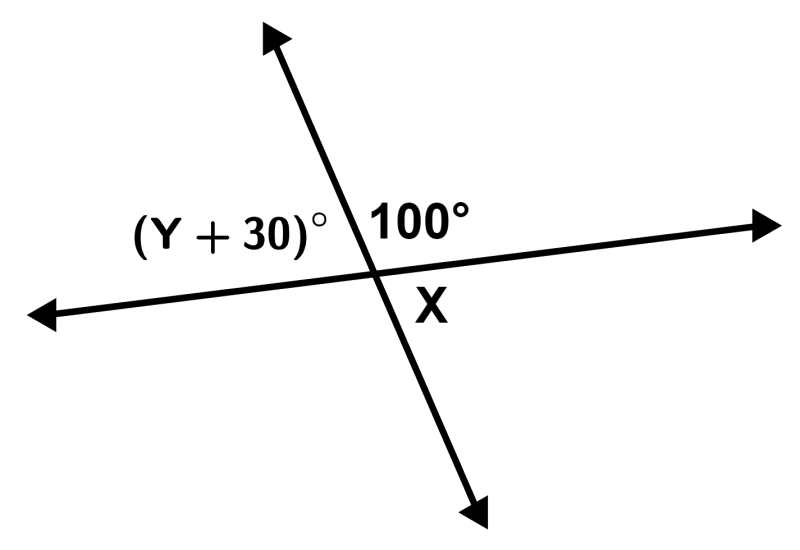
Solution: The angles ∠100° and ∠X are supplementary, so we have:
100° + ∠X = 180°
∠X = 80°
We know that the angles (Y + 30)° and X are vertical opposite, so we have:
Y + 30 = 80
Y = 50°
EXAMPLE 3
If the angles (4a-19)° and (3a + 16)° are opposite vertical angles, what is the value of a?
Solution: Since the angles are vertical opposite, we know that they are equal:
4a-19 = 3a + 16
4a-3a = 16 + 19
a = 35
The value of the given angles is:
4(35) -19 = 121°
EXAMPLE 4
If we have that the angles (2x+5)° and (3x-25)° are consecutive, what is their measure?
Solution: The consecutive angles are supplementary, so we have:
(2x + 5) + (3x-25) = 180
5x-20 = 180
5x = 200
x = 40
Therefore, the measure of the angles is:
2x+5 = 2(40)+5 = 85°
3x-25 = 3(40)-25 = 95°
See also
Interested in learning more about angles? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
