Complementary angles are defined with respect to the sum of two angles. We have a pair of complementary angles when the sum of the two angles equals 90 degrees. In other words, if the two angles add up to form a right angle, these angles are referred to as complementary angles. Here, we say that the two angles complement each other.
In this article, we will look at a more detailed definition of these types of angles along with diagrams to illustrate the concepts. In addition, we will solve some problems in which we will apply the ideas learned.
What is a complementary angle?
Complementary angles are pairs of angles that have a sum of 90 degrees. When referring to these angles, we always have to remember that they come in pairs, that is, one angle is the complement of another angle.
Although a right angle measures 90 degrees, it cannot be called a complementary angle since it does not appear in pairs. This angle is just a full angle. Similarly, three angles or more angles that have a sum equal to 90 degrees, cannot be called complementary.
EXAMPLES
The following are common examples of complementary angles:
- Two angles each measuring 45 degrees.
- Angles measuring 30 and 60 degrees.
- Angles that measure 5 and 85 degrees.
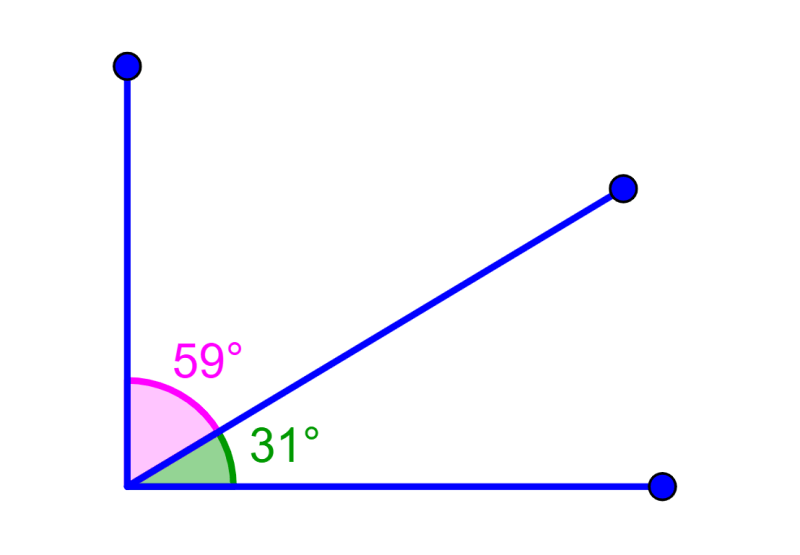
Complementary angles can be adjacent angles. For example, in the following diagram, the given angles are complementary and adjacent:
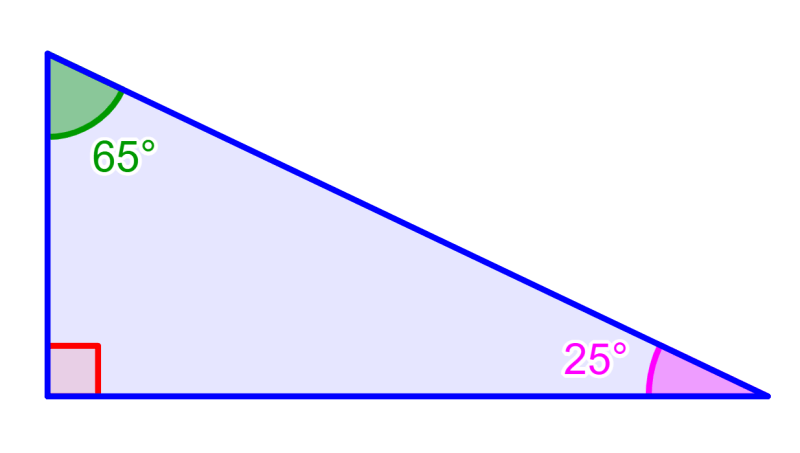
We can also have complementary angles that are not adjacent. For example, the 65° and 25° angles in the following diagram are complementary and not adjacent to each other:
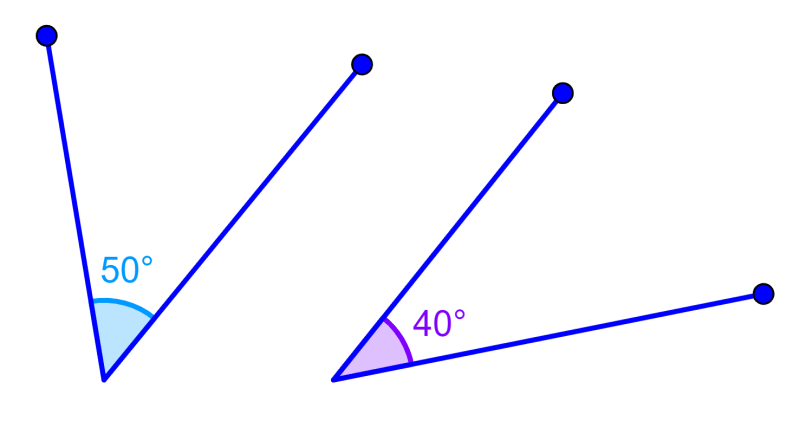
An important property of these angles is that they do not necessarily have to be part of the same figure. As long as the angles add up to 90 degrees, they will be complementary. For example, the angles in the following diagrams are complementary since they add up to 90 degrees:
How to find a complementary angle?
To find complementary angles, we have to apply the relevant arithmetic operations. We know that the sum of complementary angles is equal to 90 degrees and each of them is called the complement of the other.
Therefore, the complement of an angle is found by subtracting the angle from 90 degrees. In general terms, if we have the angle x°, its complement is equal to 90° – x°.
Suppose we have the angle 57° and we want to find its complement. The complement of the angle 57° is obtained by subtracting it from 90°: 90° – 57° = 33°. Therefore, the complementary angle of 57° is equal to 33°.
Properties of complementary angles
The following are some of the most important properties of complementary angles:
- Two angles are complementary if they add up to 90 degrees.
- Complementary angles can be adjacent or non-adjacent.
- Three or more angles cannot be complementary even if their sum is equal to 90 degrees.
- If two angles are complementary, each angle is called the “complement” or “complementary angle” of the other angle.
- Two acute angles of a right triangle are complementary.
Complementary angles – Examples with answers
We solve the following examples applying what we learned about complementary angles. Each exercise has its respective solution, where the process and reasoning used are detailed.
EXAMPLE 1
Find the complementary angle of 35°.
Solution
To find the complementary angle, we subtract the angle from 90°:
90° – 35° = 55°
The complementary angle of 35° is 55°.
EXAMPLE 2
Determine the missing angle from the following figure:
Solution
We know that the angles in a triangle add up to 180°, so we can use this and form the following equation:
A + 90° + C = 180°
A + C = 90°
Therefore, we know that angles A and C are complementary since they must add up to 90°.
A + 40° = 90°
A = 90° – 40°
A = 50°
EXAMPLE 3
If the difference between two complementary angles is 24°, find the angles.
Solution
We can use x to represent the small angle. This means that the large angle will be (90-x)°. Therefore, we have:
(90°-x)-x = 24°
90°-2x = 24°
2x = 66°
x = 33°
⇒ 90°-x = 90°-33°
= 67°
The two complementary angles are 33° and 67°.
EXAMPLE 4
Find the complementary angle of 1/3 of 90°.
Solution
We start by calculating the given angle:
90/3 = 30°
⇒ 90°-30° = 60°
Therefore, the complementary angle is 60°.
EXAMPLE 5
Find the angle that is 38° less than its complement.
Solution
We can use x to represent the angle we want to find, so the complementary angle is (90°-x). The question tells us that the difference between the angle and its complement is equal to 38°. Therefore, we have:
(90-x)-x = 38
90-2x = 38
-2x = 38-90
-2x = -38
x = 19
The angle is 19°.
Complementary angles – Practice problems
Use the following problems to practice what you have learned about complementary angles. Choose your answer and click “Verify” to check that you got the correct answer.
See also
Interested in learning more about angles? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
