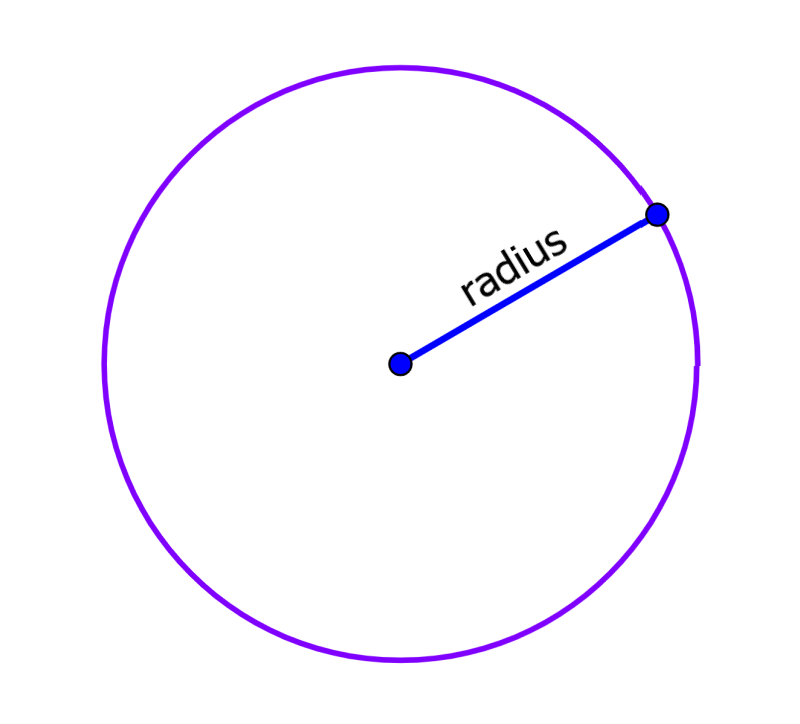
The radius of a circle is equal to the distance from the center of the circle to any point on the circumference. Usually, the radius is denoted with “R” or with “r“. This quantity is very important in geometry and appears in almost all formulas related to circles. Using the radius, we can calculate the length of the diameter, the perimeter, and the area. Similarly, we can start with any of these values to calculate the length of the radius.
Here, we will learn about the most common formulas of the circle that relate to the radius. In addition, we will learn to calculate the length of the radius using these formulas and we will see some problems.
Formulas to find the radius of a circle
The radius is the measure of the distance from the center of a circle to any point on the circumference. Using the length of the radius, we can calculate the length of the diameter, the perimeter, and the area of the circle. Similarly, we can use these expressions to find the radius.
Formula for the radius using the diameter
If we have the length of the diameter of a circle, we can find its radius using the following expression:
| $latex d=2r$ |
where d is the length of the diameter and r is the length of the radius.
Formula for the radius using the circumference
If we know the circumference, we can find the length of the radius of a circle using the following formula:
| $latex C=2\pi r$ |
where C is the circumference and r is the radius.
Formula for the radius using the area
We can use the area to calculate the radius using the following expression:
| $latex A=\pi {{r}^2}$ |
where A is the area of the circle and r is the radius.
Radius of a circle – Examples with answers
The formulas for the radius of circles are used to solve the following examples. Each example has its respective solution, where the process and reasoning used are detailed.
EXAMPLE 1
What is the radius of a circle that has a diameter of 15 m?
Solution
We can calculate the radius using the relation between of radius and diameter with the value $latex d = 15$:
$latex d=2r$
$latex r=\frac{d}{2}$
$latex r=\frac{15}{2}$
$latex r=7.5$
The radius has a length of 7.5 m.
EXAMPLE 2
If a circle has a circumference of 150 m, what is its radius?
Solution
We have $latex C =150$, so we use the ratio of the circumference and the radius with this value:
$latex C=2\pi r$
$latex r=\frac{C}{2\pi}$
$latex r=\frac{150}{2\pi}$
$latex r=23.9$
The length of the radius is 23.9 m.
EXAMPLE 3
What is the radius of a circle that has a circumference of 89 m?
Solution
Again, we have to use the relationship of the circumference and the radius. We plug the value $latex C=89$ into the circumference formula:
$latex C=2\pi r$
$latex r=\frac{C}{2\pi}$
$latex r=\frac{89}{2\pi}$
$latex r=14.2$
The length of the radius is 14.2 m.
EXAMPLE 4
What is the radius of a circle that has an area of 76 m²?
Solution
We can use the formula for the area of a circle and solve for the radius. We use the value $latex A=76$:
$latex A=\pi {{r}^2}$
$latex 76=\pi {{r}^2}$
$latex {{r}^2}=\frac{76}{\pi}$
$latex {{r}^2}=24.2$
$latex r=4.9$
The length of the radius is 4.9 m.
EXAMPLE 5
A circle has an area of 120 m². What is the length of its radius?
Solution
We use the value $latex A=120$ in the area formula and solve for $latex r$:
$latex A=\pi {{r}^2}$
$latex 120=\pi {{r}^2}$
$latex {{r}^2}=\frac{120}{\pi}$
$latex {{r}^2}=38.2$
$latex r=6.2$
The length of the radius is 6.2 m.
Radius of a circle – Practice problems
Use the following problems to practice applying the formula for the radius of circles. If you need help with these problems, you can look at the solved examples above.
See also
Interested in learning more about circles? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
