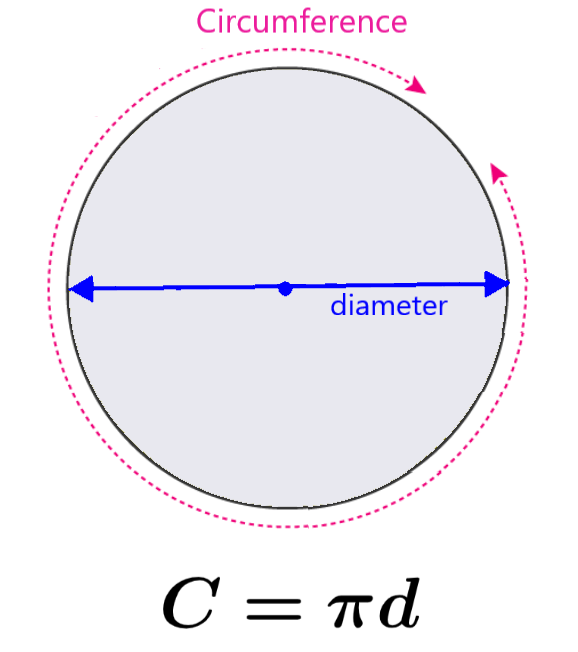
The circumference of a circle defines the length of the contour of the circle. The circumference is also referred to as the perimeter of the circle since it is a measure of the limits of the circle. The circumference can be calculated using the length of the diameter or the length of the radius and the constant π.
Here, we will learn about the circumference of the circle in more detail. We will discover what its formula is and we will learn how to derive it. In addition, we will know about the origin of the constant π. Finally, we will solve some problems where we will apply the circumference formula.
Formula for the circumference of a circle
The circumference represents the length obtained by going one complete revolution around the circle. This length can be obtained by using the length of the diameter or radius of the circle and the constant pi.
Recall that we use the Greek letter π to represent this constant and that it has an approximate value of 3.141592… To obtain a formula for the circumference, we can consider the following circle:
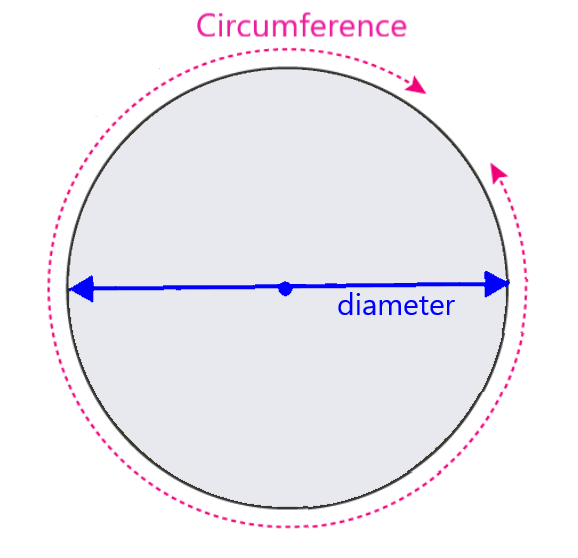
In the diagram, we can see that the circumference is the distance around the circle. Also, we can see that the diameter is the distance that passes through the center of the circle and connects two opposite parts of the circumference.
The constant π represents the ratio of the circumference of the circle to the diameter. This means that when we divide the circumference of any circle by the diameter, we get the constant π. We can express this relationship with the following formula:
$latex \frac{C}{d}=\pi$
where, C represents the circumference and d is the length of the diameter of the circle. Also, we can rewrite this expression as follows:
| $latex C=\pi d$ |
Circumference of a circle using the radius
The circumference of a circle can also be calculated using the length of the radius. For this, we use the relation $latex d = 2r$. By rewriting the expression, we have:
| $latex C=2\pi r$ |
Circumference of a circle – Examples with answers
The following examples are solved using the formulas for the circumference of circles. It is recommended that you solve the exercises yourself before looking at the solution.
EXAMPLE 1
What is the circumference of a circle that has a diameter of 5 m?
Solution
We have the length of the diameter $latex d=5$. Therefore, we use the first formula:
$latex C=\pi d$
$latex C=\pi (5)$
$latex C=15.7$
The circumference is equal to 15.7 m.
EXAMPLE 2
If a circle has a diameter of 9 m. What is the length of its circumference?
Solution
We can use the first formula for the circumference with the value $latex d=9$:
$latex C=\pi d$
$latex C=\pi (9)$
$latex C=28.3$
The circumference is equal to 28.3 m.
EXAMPLE 3
What is the length of the circumference of a circle that has a radius of 4 m?
Solution
Here, we have the length of the radius instead of the diameter. We can use the second formula with the value $latex r=4$:
$latex C=2\pi r$
$latex C=2\pi (4)$
$latex C=50.3$
The length of the circumference is 25.1 m.
EXAMPLE 4
A circle has a radius of 11 m. What is its circumference?
Solution
We use the second formula for the circumference with the value $latex r=11$. Therefore, we have:
$latex C=2\pi r$
$latex C=2\pi (11)$
$latex C=69.1$
The circumference is equal to 69.1 m.
EXAMPLE 5
If a circle has a circumference of 80 m, what is the length of its diameter?
Solution
Here, we start with the value of the circumference and want to find the length of the diameter, so we use the value $latex C = 80$ in the formula and solve for d:
$latex C=\pi d$
$latex 80=\pi d$
$latex d=\frac{80}{\pi}$
$latex d=25.5$
The length of the diameter is equal to 25.5 m.
Circumference of a circle – Practice problems
Use the formulas for the circumference of circles to solve the following problems. If you need help with this, you can look at the solved examples above.
See also
Interested in learning more about circles? Take a look at these pages: