The area of a circle is the region occupied by the circle in the two-dimensional plane. We can easily determine this area using the formula A=πr², where r is the length of the radius of the circle and where π is a mathematical constant with an approximate value of 3.14.
Here, we will explore the area of a circle in more detail. We will how to prove the formula for the area of a circle. In addition, we will look at other methods for calculating this area.
Finding the area of a circle using the radius
Remember that a circle is a closed geometric figure. Technically, a circle is a set of points located at a fixed distance from a central point. The fixed distance from the point is the radius of the circle.
The radius is the line that joins the center of the circle to the outer limit. The following is a circle with radius r:
The area of a circle can be calculated with the following formula:
| A=πr² |
where, r is the length of the radius and π is the value of pi, $latex \pi = \frac{22}{7}$ or approximately 3.14.
Proof of the formula for the area of a circle
We can derive the formula for the area of circles by dividing the circle into several sectors and arranging the sectors as shown in the following figure:
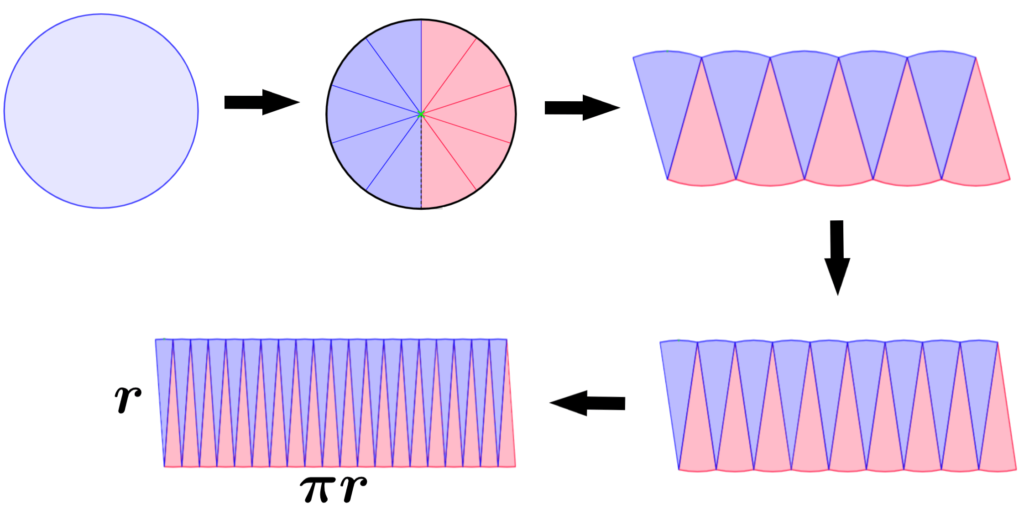
The area of the circle is equal to the area of the parallelogram formed by the cut sectors of the circle. Since all sectors have the same area, each sector will have the same arc length. If the number of sectors cut from the circle is increased, the parallelogram will eventually look like a rectangle with a base equal to πr and a height equal to r.
We know that the area of a rectangle equals base times height, so we have:
$latex A=\pi r\times r$
$latex A=\pi {{r}^2}$
How to find the area of a circle using the diameter?
To find the area of a circle when we know the length of the diameter, we have to find the length of the radius using the diameter and then use it in the formula for the area of a circle.
Let’s remember that the diameter is equal to $latex d=2r$. That is, the length of the radius is equal to the length of the diameter divided by 2.
Then, we can use the standard formula for the area of a circle with the length of the radius found:
$latex A=\pi r^2$
Alternatively, we can determine a formula for the area of a circle in terms of the diameter.
Therefore, recalling that the formula for a circle is as follows:
$latex A=\pi r^2$
we can substitute the following relationship into the formula:
$latex d=2r$
$latex r=\frac{d}{2}$
Then, we have:
$latex A=\pi r^2$
$latex A=\pi (\frac{d}{2})^2$
| $$A=\pi (\frac{d^2}{4})$$ |
where d is the diameter of the circle and A is its area.
How to find the area of n circle using the circumference?
We can find the area of a circle by determining the length of the radius from the circumference and then using that length in the standard formula for the area of a circle.
Then, we remember that the circumference can be written as follows:
$latex C=2\pi r$
Therefore, to find the length of the radius, we can divide the circumference by 2π. Then, we use the Area of a Circle formula with the radius found:
$latex A=\pi r^2$
Alternatively, we can derive a formula for the area of a circle in terms of the circumference. So, we start with the standard formula for the area of a circle:
$latex A=\pi r^2$
Now, we can substitute the following equation:
$latex C=2\pi r$
$latex r=\frac{C}{2\pi}$
Then, we have:
$latex A=\pi r^2$
$latex A=\pi (\frac{C}{2\pi})^2$
$latex A=\pi (\frac{C^2}{4\pi^2})$
| $$A= \frac{C^2}{4\pi}$$ |
where C is the circumference and A is the area of the circle.
Area of a circle – Examples with answers
EXAMPLE 1
What is the area of a circle that has a radius of 5 m?
Solution
We can use the first formula for the area with the value $latex r=5$. Therefore, we have:
$latex A=\pi {{r}^2}$
$latex A=\pi {{(5)}^2}$
$latex A=\pi (25)$
$latex A=78.5$
The area of the circle is 78.5 m².
EXAMPLE 2
A circle has a radius of 12 m. What is its area?
Solution
Here, we have the radius $latex r=12$, so we use this value in the first formula for the area:
$latex A=\pi {{r}^2}$
$latex A=\pi {{(12)}^2}$
$latex A=\pi (144)$
$latex A=452.4$
The area of the circle is 452.4 m².
EXAMPLE 3
What is the area of a circle that has a diameter of 10 m?
Solution
In this case, we have the diameter instead of the radius, so we use the second formula with the value $latex d=10$. Therefore, we have:
$latex A=\pi(\frac{{{d}^2}}{4})$
$latex A=\pi(\frac{{{(10)}^2}}{4})$
$latex A=\pi(\frac{100}{4})$
$latex A=\pi(25)$
$latex A=78.5$
The area of the circle is 78.5 m².
EXAMPLE 4
If a circle has a diameter of 20 m. What is its area?
Solution
Again, we use the diameter in the second formula with the value. Therefore, we substitute the value $latex d=20$:
$latex A=\pi(\frac{{{d}^2}}{4})$
$latex A=\pi(\frac{{{(20)}^2}}{4})$
$latex A=\pi(\frac{400}{4})$
$latex A=\pi(100)$
$latex A=314.16$
The area of the circle is 314.16 m².
EXAMPLE 5
A circle has an area of 150 cm². What is the length of its radius?
Solution
In this case, we start with the area and want to find the length of the radius. Therefore, we use the value $latex A=150$ in the first formula and solve for r:
$latex A=\pi {{r}^2}$
$latex 150=\pi {{r}^2}$
$latex {{r}^2}=\frac{150}{\pi}$
$latex {{r}^2}=47.75$
$latex r=6.91$
The radius of the circle is 6.91 cm.
EXAMPLE 6
Determine the length of the diameter of a circle that has an area of $latex 55~{{in}^2}$.
Solution
This example is similar to the previous one, so we have to use the given area value and solve for d:
$$A=\pi (\frac{d^2}{4})$$
$$55=\pi (\frac{d^2}{4})$$
$latex 220=\pi~{{d}^2}$
$latex d^2=70.028$
$latex d=8.368$
The diameter of the circle has a length of 8.368 in.
EXAMPLE 7
What is the area of a circle that has a circumference of 25 inches?
Solution
We are going to use the first method. Therefore, we find the length of the radius as follows:
$latex r=\frac{C}{2\pi}$
$latex r=\frac{25}{2\pi}$
$latex r=3.979$
Now, we use the formula for the area of a circle in terms of the radius:
$latex A=\pi~r^2$
$latex A=\pi~(3.979)^2$
$latex A\approx 49.739$
The area of the circle is 49.739 inches squared.
EXAMPLE 8
Find the circumference of a circle that has an area of $latex 88~{{in}^2}$.
Solution
We can solve this problem by using the formula for the area of a circle in terms of the circumference and solving for C:
$$A= \frac{C^2}{4\pi}$$
$$88= \frac{C^2}{4\pi}$$
$latex 352\pi={{C}^2}$
$latex C=33.254$
The circumference of the circle is equal to 33.254 in.
Area of a circle – Practice problems
If a circle that has an area of $latex 60 ~{{m}^2}$, what is its circumference?
Write the answer in decimal places.
See also
Interested in learning more about circles? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
