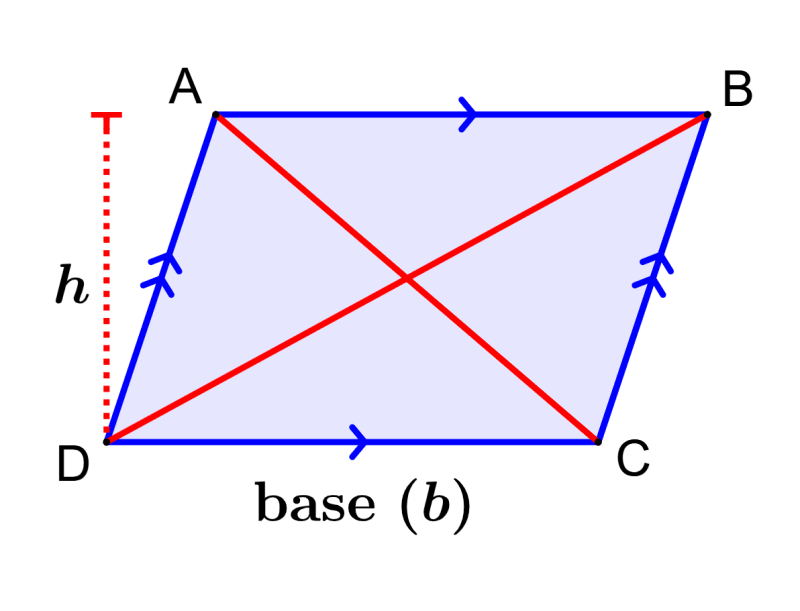
A parallelogram is a two-dimensional figure that has sides that are parallel to each other. The parallelogram is a type of polygon that has four sides (called a quadrilateral), where the pair of parallel sides are equal in length. In addition, the opposite interior angles of a parallelogram have the same measures. The sum of the adjacent angles of a parallelogram is equal to 180 degrees.
Here, we will learn about the fundamental properties of parallelograms. Also, we will look at the formulas for the most important parallelograms and use them to solve some problems.
Definition of a parallelogram
A parallelogram is a quadrilateral that has the main characteristic of having two pairs of parallel sides. The opposite sides of the parallelogram have the same length and the opposite angles have the same measure. Also, the internal angles on the same side of the transversal are supplementary. The sum of all the interior angles is equal to 360 degrees.
A square and a rectangle are two figures that have properties similar to a parallelogram.
If the sides of a parallelogram are congruent or equal to each other, then the figure is a rhombus.
The following is the image of a parallelogram:
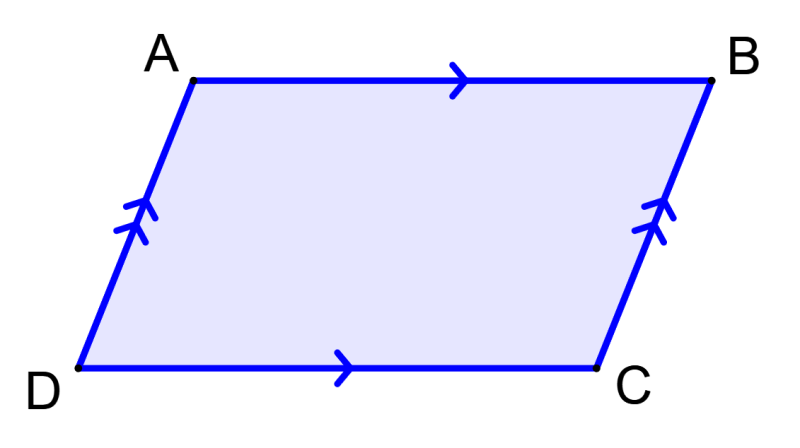
In the figure, we can see that AB and CD are parallel, as well as sides AD and BC. Also, sides AB and CD are equal and sides AD and BC are also equal.
Angle A is equal to angle C and angle B is equal to angle D. Also, angles A and D are supplementary since these angles are located on the same side of the transversal. Similarly, angles B and C are supplementary. Therefore, these angles add up to 180°.
Fundamental properties of parallelograms
The fundamental properties of parallelograms are as follows:
- The opposite sides are parallel.
- The opposite sides are congruent (they have the same length).
- Consecutive angles are supplementary.
- If one of the angles is a right angle, then the other angles will also be right angles.
- The two diagonals bisect each other.
- Each diagonal bisects the parallelogram into two congruent triangles.
- The sum of the square of the lengths of all the sides of the parallelogram is equal to the sum of the square of its diagonals.
Important formulas of parallelograms
The formulas for the area and perimeter of a parallelogram can be used to solve problems.
Area of a parallelogram
The area of the parallelogram is the region occupied by the figure in the two-dimensional plane. The following is the formula to find the area of the parallelogram:
| Area = Base × Height $latex A=b\times h$ |
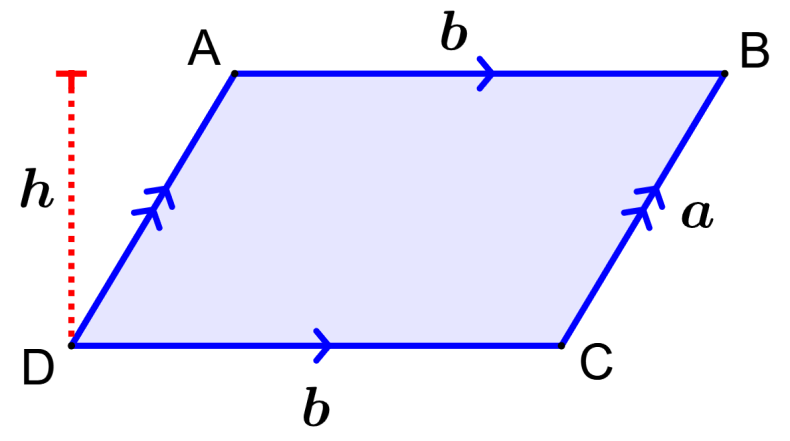
Perimeter of a parallelogram
The perimeter of any shape is the total distance covered around the shape. Similarly, the perimeter of the parallelogram is the total distance of the limits of the parallelogram. To calculate the perimeter, we need to know the lengths of its sides. A parallelogram has its opposite sides equal in length. Therefore, the perimeter formula is:
| $latex p=2(a+b)$ |
where a and b are the lengths of the sides of the parallelogram.
Examples of parallelograms problems
EXAMPLE 1
What is the area of a parallelogram that has sides of length 13 m and 15 m?
Solution: We have the following data:
- Base, $latex b=13$ m
- Height, $latex h=15$ m
Therefore, we use the area formula with these values:
$latex A=bh$
$latex A=(13)(15)$
$latex A=195$
The area of the parallelogram is 195 m².
EXAMPLE 2
What is the perimeter of a parallelogram that has sides of length 21 cm and 22 cm?
Solution: We have the following values:
- Side 1, $latex a=21$ m
- Side 2, $latex b=22$ m
Therefore, we use the perimeter formula with these values:
$latex p=2(a+b)$
$latex p=2(21+22)$
$latex p=2(43)$
$latex p=86$
The perimeter of the parallelogram is 86 m.
See also
Interested in learning more about parallelograms? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
