The area of a parallelogram is the region covered by a parallelogram in a 2D plane. A parallelogram is a two-dimensional figure with four sides and can be considered as a special case of a quadrilateral. The sum of the interior angles of a parallelogram is 360 degrees. In addition, a parallelogram has two pairs of parallel sides with equal measurements. Since it is a two-dimensional figure, it has an area and a perimeter.
Here, we will learn about the methods we can use to calculate the area of a parallelogram. We will look at the formulas to calculate the area and we will apply them to solve some problems.
How to find the area of a parallelogram
To find the area of a parallelogram, we multiply the length of the perpendicular base by its height. We have to bear in mind that the base and the height of the parallelogram are perpendicular to each other, while the lateral side of the parallelogram is not perpendicular to the base.
Therefore, we can use a dashed line to represent the height of the parallelogram:
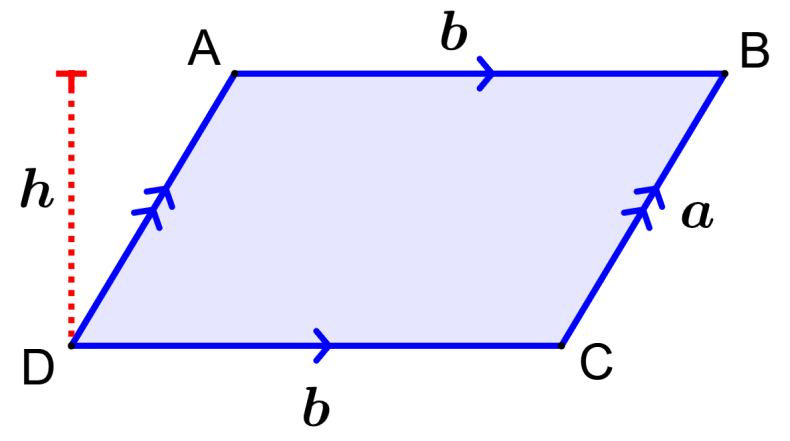
Therefore, we have the following formula to calculate the area of a parallelogram:
| $latex A=bh$ |
where b is the length of the base and h is the length of the height.
Area of a parallelogram without using its height
If we do not know the height of a parallelogram, we can use trigonometry to find its area with the following formula:
| $latex A=ab\sin(x)$ |
where a and b are the lengths of the sides of the parallelogram and x is the measure of the angle between the sides.
Area of a parallelogram using its diagonals
The area of any parallelogram can also be calculated with the lengths of its diagonals by using the following formula:
| $latex A=\frac{d_{1}\times d_{2}\sin(y)}{2}$ |
where, $latex d_{1}, ~ d_{2}$ are the lengths of the diagonals and y is the angle of intersection of the diagonals.
Area of a parallelogram – Examples with answers
The different methods of calculating the area of a parallelogram are used to solve the following examples. Each example has its answer, but it is recommended that you try to solve the examples yourself before looking at the answer.
EXAMPLE 1
A parallelogram has bases with a length of 12 m and a height of 11 m. What is its area?
Solution
We have the following values:
- Base, $latex b=12$ m
- Height, $latex h=11$ m
We use the area formula with these values:
$latex A=bh$
$latex A=(12)(11)$
$latex A=132$
The area of the parallelogram is 132 m².
EXAMPLE 2
What is the area of a parallelogram that has a base of 15 m and a height of 20 m?
Solution
We have the following information:
- Base, $latex b=15$ m
- Height, $latex h=20$ m
We use the area formula with these values:
$latex A=bh$
$latex A=(15)(20)$
$latex A=300$
The area of the parallelogram is 300 m².
EXAMPLE 3
If a parallelogram has sides with lengths of 14 m and 12 m and the angle between them is 60°, what is their area?
Solution
We have the following information:
- Side 1, $latex a=14$ m
- Side 2, $latex b=12$ m
- Angle, $latex x=60$°
We use the second formula with this information:
$latex A=ab\sin(x)$
$latex A=(14)(12)\sin(60°)$
$latex A=(168)(0.866)$
$latex A=145.5$
The area of the parallelogram is 145.5 m².
EXAMPLE 4
A parallelogram has diagonals with lengths of 10 m and 9 m. If the angle of intersection of the diagonals is 30°, what is their area?
Solution
We have the following values:
- Diagonal 1, $latex d_{1}=10$ m
- Diagonal 2, $latex d_{2}=9$ m
- Angle, $latex y=30$°
We can use these values in the third formula:
$latex A=\frac{d_{1}\times d_{2}\sin(y)}{2}$
$latex A=\frac{10\times 9\sin(30°)}{2}$
$latex A=\frac{(90)(0.5)}{2}$
$latex A=\frac{45}{2}$
$latex A=22.5$
The area of the parallelogram is 22.5 m².
EXAMPLE 5
The area of a parallelogram is equal to 182 m². If its height is 13 m, what is the length of its base?
Solution
We have the following values:
- Area, A = 182 m²
- Height, h = 13 m
We use the area formula with these values and solve for the base, b:
$latex A=bh$
$latex 182=13b$
$latex b=14$
The length of the base is 14 m.
Area of a parallelogram – Practice problems
Solve the following problems using the methods seen to calculate the area of parallelograms. If you need help with this, you can look at the solved examples above.
See also
Interested in learning more about parallelograms? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
