To find the points of intersection of two circles, we start by finding the equation of the common chord. This is accomplished by subtracting the equations of the circles to obtain a linear equation. Then, we substitute this equation into one of the equations of the circles and solve.
Below, we will learn the process we can use to find the points of intersection of two circles. Then, we will solve some practice examples.
How to find the intersection points of two circles
Two circles can intersect at two different points, as shown in the following diagram:
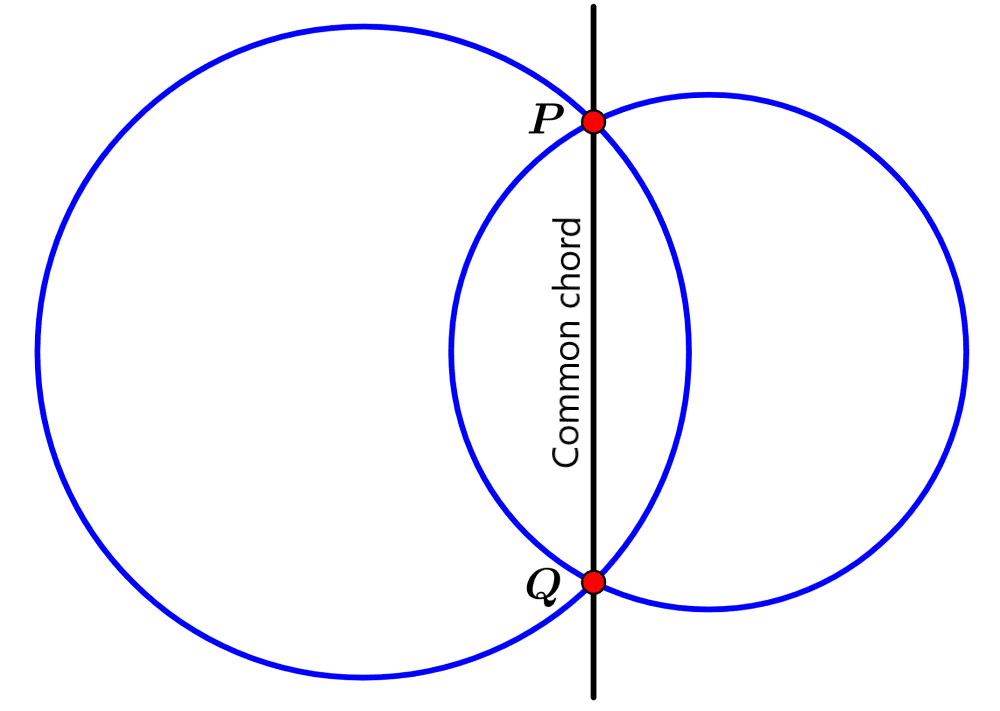
The coordinates of the intersection points, P and Q, satisfy the equations of both circles. In addition, the coordinates of P and Q also satisfy the equation of the common chord.
Considering this, we can find the coordinates of the intersection points of two circles, by following the steps below:
1. Find the equation of the common chord.
This equation is a linear equation found by subtracting the equations of the circles so that we eliminate the quadratic terms.
2. Solve the equation from step 1 for one of the variables.
3. Substitute the equation from step 2 into one of the equations of the circles.
By solving this, we will find both x-coordinates or y-coordinates of the points.
4. Use the coordinates from step 3 in any of the equations of the circles to find the missing coordinates.
Intersection of two circles – Examples with answers
EXAMPLE 1
What are the coordinates of the intersection points of the circles with equations $latex x^2+y^2-3x+5y-4=0$ and $latex x^2+y^2-x+4y-7=0$?
Solution
Step 1: By subtracting the equations of the circles, we can find the equation of the common chord:
$latex x^2+y^2-3x+5y-4=0$
$latex x^2+y^2-x+4y-7=0~(-$
______________________
$latex -2x+y+3=0$
Step 2: Solving the equation for y, we have:
$latex y=2x-3$
Step 3: Substituting the equation from step 2 into the equation of the second circle, we have:
$latex x^2+y^2-x+4y-7=0$
$$x^2+(2x-3)^2-x+4(2x-3)-7=0$$
$latex 5x^2-5x-10=0$
$latex 5(x-2)(x+1)=0$
Solving, we have $latex x=2$ and $latex x=-1$.
Step 4: When $latex x=2$, we have $latex y=1$ and when $latex x=-1$, we have $latex y=-5$.
Then, the intersection points of the circles are $latex (-1,~-5)$ and $latex (2, 1)$.
EXAMPLE 2
Determine the coordinates of the intersection points of the circles with equations $latex x^2+y^2-5x+3y-4=0$ and $latex x^2+y^2-4x+6y-12=0$.
Solution
Step 1: By subtracting the equations of the circles, we have:
$latex x^2+y^2-5x+3y-4=0$
$latex x^2+y^2-4x+6y-12=0~(-$
______________________
$latex -x-3y+8=0$
Step 2: Solving the equation for x, we have:
$latex x=-3y+8$
Step 3: Substituting the equation from step 2 into the equation of the first circle, we have:
$latex x^2+y^2-5x+3y-4=0$
$$(-3y+8)^2+y^2-5(-3y+8)+3y-4=0$$
$latex 10y^2-30y+20=0$
$latex 10(y-2)(y-1)=0$
Solving, we have $latex y=2$ and $latex y=1$.
Step 4: When $latex y=2$, we have $latex x=2$ and when $latex y=1$, we have $latex x=5$.
Then, the intersection points of the circles are $latex (2, ~2)$ and $latex (5,~ 1)$.
EXAMPLE 3
What are the intersection points of the circles $latex x^2+y^2-4x+3y+5=0$ and $latex x^2+y^2-6x+5y+9=0$?
Solution
Step 1: Let’s find the equation of the common chord by subtracting the equations of the circles:
$latex x^2+y^2-4x+3y+5=0$
$latex x^2+y^2-6x+5y+9=0~(-$
______________________
$latex 2x-2y-4=0$
Step 2: We can simplify the equation obtained by dividing by 2, and solving for x, we have:
$latex x-y-2=0$
$latex x=y-2$
Step 3: Let’s substitute the equation from step 2 into the equation of the first circle. Then, we have:
$latex x^2+y^2-4x+3y+5=0$
$$(y-2)^2+y^2+4(y-2)+3y+5=0$$
$latex 2y^2+3y+1=0$
$latex (2y+1)(y+1)=0$
Solving, we have $latex y=-\frac{1}{2}$ and $latex y=-1$.
Step 4: When $latex y=-\frac{1}{2}$, we have $latex x=1~\frac{1}{2}$ and when $latex y=-1$, we have $latex x=1$.
Therefore, the points of intersection of the circles are $latex (1 ~\frac{1}{2},~-\frac{1}{2})$ and $latex (1, -1)$.
EXAMPLE 4
Find the coordinates of the intersection points of the circles $latex x^2+y^2+3x-2y-7=0$ and $latex x^2+y^2+x-y-8=0$.
Solution
Step 1: Subtracting the equations of the circles, we have:
$latex x^2+y^2+3x-2y-7=0$
$latex x^2+y^2+x-y-8=0~(-$
______________________
$latex 2x-y+1=0$
Step 2: Solving the equation for y, we have:
$latex y=2x+1$
Step 3: Using the equation from step 2 in the equation of the second circle, we have:
$latex x^2+y^2+x-y-8=0$
$$x^2+(2x+1)^2+x-(2x+1)-8=0$$
$latex 5x^2+3x-8=0$
$latex (5x+8)(x-1)=0$
Solving, we have $latex x=-\frac{8}{3}$ and $latex x=1$.
Step 4: When $latex x=-\frac{8}{3}$, we have $latex y=-\frac{11}{5}$ and when $latex x=1$, we have $latex y=3$.
Therefore, the points of intersection of the circles are $latex (-\frac{8}{3},~\frac{11}{5})$ and $latex (1, 3)$.
EXAMPLE 5
Find the coordinates of the intersection points of the circles with equations $latex x^2+y^2-3x+13y-48=0$ and $latex x^2+y^2+x-3y=0$.
Solution
Step 1: We find the equation of the common chord by subtracting the equations of the circles:
$latex x^2+y^2-3x+13y-48=0$
$latex x^2+y^2+x-3y=0~~(-$
______________________
$latex -4x+16y-48=0$
Step 2: We can simplify the equation obtained by dividing by 4, and solving for x, we have:
$latex -x+4y-12=0$
$latex x=4y-12$
Step 3: Substituting the equation from step 2 into the equation of the second circle, we have:
$latex x^2+y^2+x-3y=0$
$$(4y-12)^2+y^2+(4y-12)-3y=0$$
$latex 17y^2-95y+132=0$
$latex (17y-44)(y-3)=0$
Solving, we have $latex y=\frac{44}{17}$ and $latex y=3$.
Step 4: When $latex y=\frac{44}{17}$, we have $latex x=-\frac{28}{17}$ and when $latex y=3$, we have $latex x=0$.
Therefore, the points of intersection of the circles are $latex (-\frac{28}{17},~\frac{44}{17})$ and $latex (0, 3)$.
Intersection of two circles – Practice problems


The circles $latex x^2-10x+y^2-8y+36=0$ and $latex x^2-2x+y^2-12y+32=0$ have only one point of intersection.
Write the coordinates of the point in the input box.
See also
Interested in learning more about circles? You can take a look at these pages:



