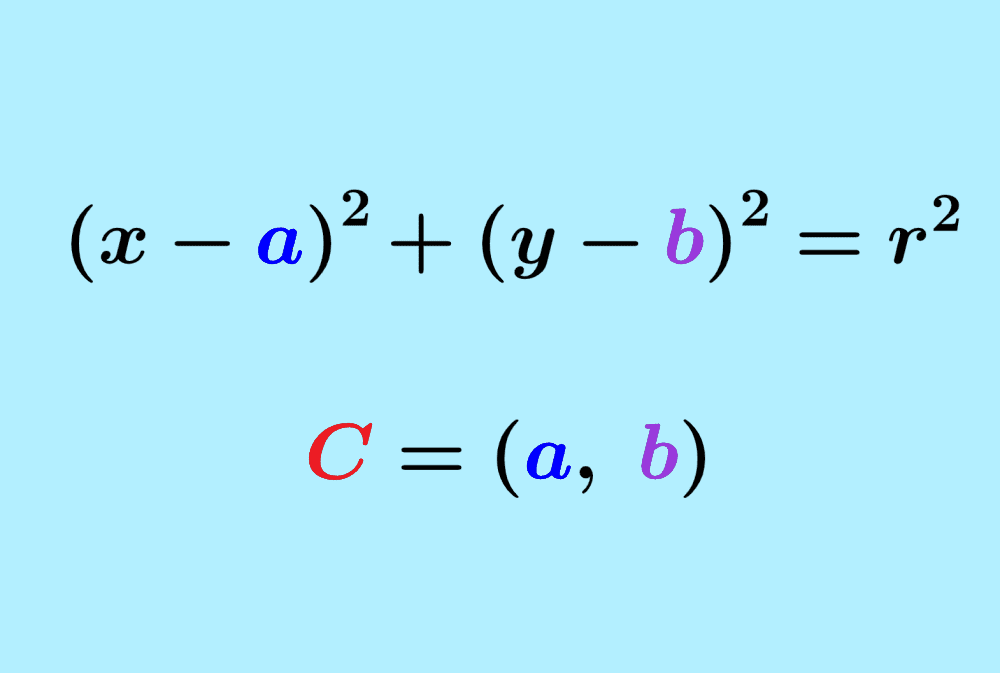To find the radius and coordinates of the center of a circle when we have its equation written in general form, we have to write the equation in its standard form. This is done by completing the square of both x, and y. Once we have the standard form, we can identify the center and radius easily.
In this article, we will learn how to find the radius and center of a circle when we have its equation in general form. We will look at some practice problems to apply what we have learned.
Steps to find the radius and center of a circle
To find the radius and center of a circle, let’s start by finding the standard equation of a circle.
Suppose we have a circle with center $latex C=(a,~b)$ and radius $latex r$. Moreover, the point $latex P=(x,~y)$ lies on the circumference of the circle.
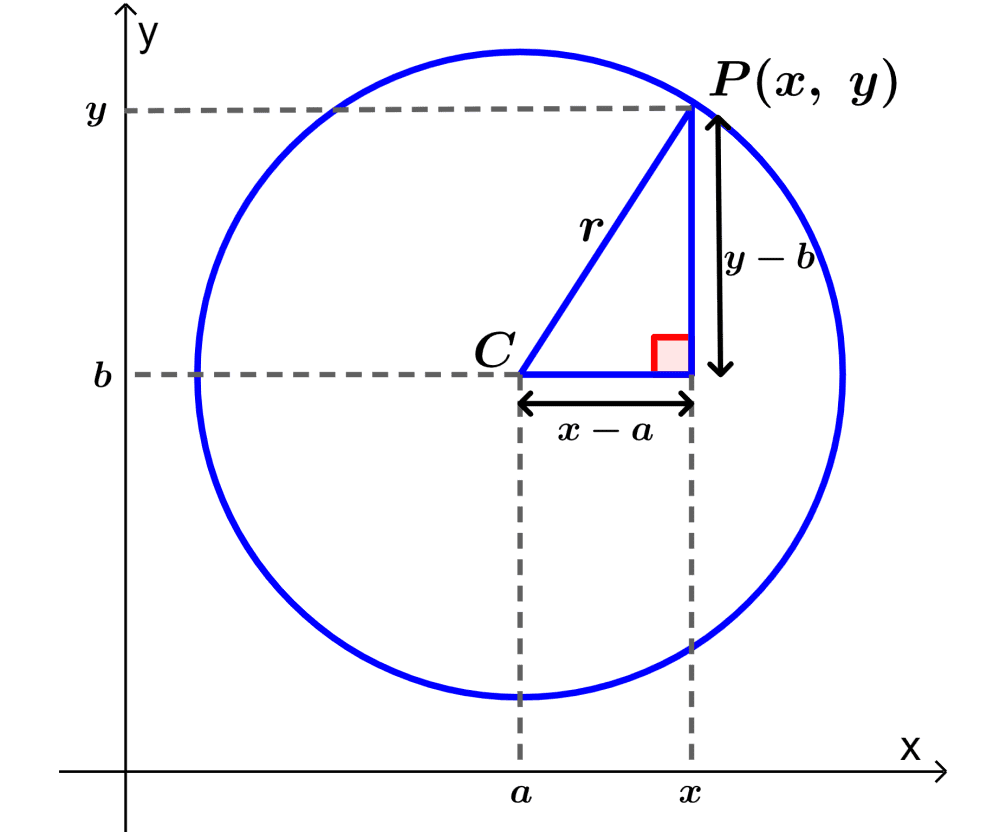
If we use the formula for the distance between two points, we have:
$$ r=\sqrt{(x-a)^2+(y-b)^2}$$
When squaring, we have:
$$ r^2=(x-a)^2+(y-b)^2$$
This is the standard form of the equation of the circle. In this form, $latex r$ is the radius and $latex (a, ~b)$ is the center of the circle.
When we expand and simplify this equation, we have the general equation of the circle:
$$ x^2+y^2-2ax-2by+c=0$$
where, $latex c=a^2+b^2-r^2$.
Then, if we have the equation of a circle given in its general form, we can find its center and radius as follows:
1. Write the equation of the circle in its standard form, $latex r^2=(x-a)^2+(y-b)^2$.
We can accomplish this by completing the square of x and y.
2. Take the square root of $latex r^2$ to get the radius of the circle.
3. The center of the circle is equal to $latex (a, ~b)$.
The standard form $latex r^2=(x-a)^2+(y-b)^2$ gives us the center of the circle.
Radius and center of a circle using its equation – Examples with answers
EXAMPLE 1
Find the radius and coordinates of the center of a circle having the equation $latex (x-5)^2+(y+3)^2=16$.
Solution
In this example, we have the equation of the circle given in its standard form. Then, we can obtain the coordinates of the center and the radius by comparing it with the equation:
$latex (x-a)^2+(y-b)^2=r^2$
Therefore, we see that $latex a=5$ and $latex b=-3$, so the center is $latex (5,~-3)$.
To find the radius, we have to take the square root of 16, which is equal to 4, so the radius is $latex r=4$.
EXAMPLE 2
What is the center and radius of a circle having the equation $latex (x+7)^2+(y-4)^2+6=10$?
Solution
This example is similar to the previous one, with the difference that we have to simplify the given equation first. Then, we have:
$latex (x+7)^2+(y-4)^2+6=10$
$latex (x+7)^2+(y-4)^2=4$
Now, we compare it with the standard form:
$latex (x-a)^2+(y-b)^2=r^2$
Then, we have $latex a=-7$ and $latex b=4$, so the center is $latex (5,~-3)$.
The radius is equal to $latex r=2$.
EXAMPLE 3
Find the radius and center of a circle having the equation $latex x^2+y^2+2x-4y-4=0$.
Solution
In this case, we have the equation of the circle in its general form. Then, we have to start by converting the equation to standard form.
For this, we complete the square of both x and y and we have:
$latex x^2+y^2+2x-4y-4=0$
$latex x^2+2x+y^2-4y-4=0$
$$(x+1)^2-1+(y-2)^2-4-4=0$$
$latex (x+1)^2+(y-2)^2=9$
Now that we have the equation of the circle in its standard form, we can easily see that the center is $latex (-1, ~2)$ and its radius is $latex r=3$.
EXAMPLE 4
What are the coordinates of the center and radius of the circle with the equation $latex x^2+y^2-4x-2y+1=0$?
Solution
To find the radius and the coordinates of the center, we have to find the standard form of the equation of the circle. Then, we complete the square of both variables:
$latex x^2+y^2-4x-2y+1=0$
$latex x^2-4x+y^2-2y+1=0$
$$(x-2)^2-4+(y-1)^2-1+1=0$$
$latex (x-2)^2+(y-1)^2=4$
The center of the circle is $latex (2, ~1)$ and its radius is $latex r=2$.
EXAMPLE 5
Find the radius and center of a circle having the equation $latex x^2+y^2-2x-8y+8=0$.
Solution
Let’s complete the square of both variables to find the standard form of the equation of the given circle:
$latex x^2+y^2-2x-8y+8=0$
$latex x^2-2x+y^2-8y+8=0$
$$(x-1)^2-1+(y-4)^2-16+8=0$$
$latex (x-1)^2+(y-4)^2=9$
The coordinates of the center of the circle are $latex (1, ~4)$ and its radius is $latex r=3$.
EXAMPLE 6
What is the radius and center of a circle represented by the equation $latex 9x^2+9y^2-12x+18y+4=0$?
Solution
To simplify the solution of this problem, we can divide the whole equation by 9:
$$ x^2+y^2-\frac{4}{3}x+2y+\frac{4}{9}=0$$
Rearranging the equation and completing the square of x and y, we have:
$$ x^2-\frac{4}{3}x+y^2+2y+\frac{4}{9}=0$$
$$ \left(x-\frac{2}{3}\right)^2-\frac{4}{9}+(y+1)^2-1+\frac{4}{9}=0$$
$$ \left(x-\frac{2}{3}\right)^2+(y+1)^2=1$$
The coordinates of the center of the circle are $latex(\frac{2}{3},~-1)$ and the radius is 1.
Radius and center of a circle – Practice problems
What are the coordinates of the center of the following circle? $$x^2+16x+y^2-10y+89=10$$
Write the coordinates in the input box.
See also
Interested in learning more about circles? You can take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
