The interior angles of a trapezoid always measure 360°. We have three main types of trapezoids: isosceles trapezoid, scalene trapezoid, and right trapezoid. Depending on the type of trapezoid, we can use a different method to find all the measures of its internal angles.
Here, we will learn how to calculate the interior angle measures of various types of trapezoids using examples.
Sum of interior angles of a trapezoid
A trapezoid is a quadrilateral that has one pair of opposite parallel sides. The opposite parallel sides are called the bases of the trapezoid and the other two sides are the lateral sides. The trapezoid is a closed figure that has four sides and four corners.
The sum of the four interior angles of a trapezoid is always equal to 360°. We can verify this using the following formula for interior angles of a polygon:
| $latex (n-2)\times 180$° |
where, n is the number of sides of the polygon. Therefore, for a trapezoid, we have:
$latex (n-2)\times 180$°
$latex =(4-2)\times 180$°
$latex =(2)\times 180$°
$latex =360$°
Alternatively, we can also use the following diagram. We see that we can divide the trapezoid into two triangles, so the sum of the interior angles in a trapezoid is equal to the sum of the interior angles of two triangles.
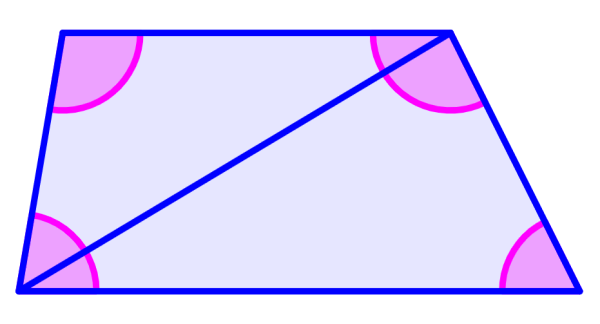
Calculate the interior angles of an isosceles trapezoid
An isosceles trapezoid is characterized by having its lateral sides of the same length. Furthermore, these trapezoids also have two pairs of equal interior angles. That means that to calculate the measure of an internal angle of an isosceles trapezoid, we need to have the measure of an angle of the trapezoid.
EXAMPLE 1
Find the measures of all the interior angles of the following isosceles trapezoid.
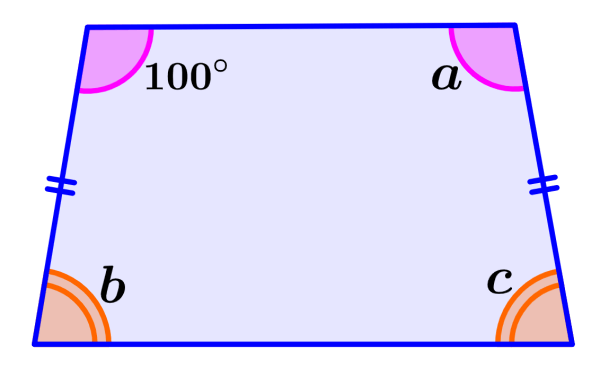
Solution: Angles that have the same color and the same number of lines are equal. Therefore, we know that angle a measures 100°. Similarly, we know that angles b and c also have the same measure. Therefore, to find the missing angles, we have to add the known angles and subtract from 360°:
100°+100° = 200°
⇒ 360°-200° = 160°
Since the two angles are equal, we divide the result by 2 and we get 80°. This is the measure of angles b and c.
EXAMPLE 2
Determine the measures of the missing angles in the isosceles trapezoid below.
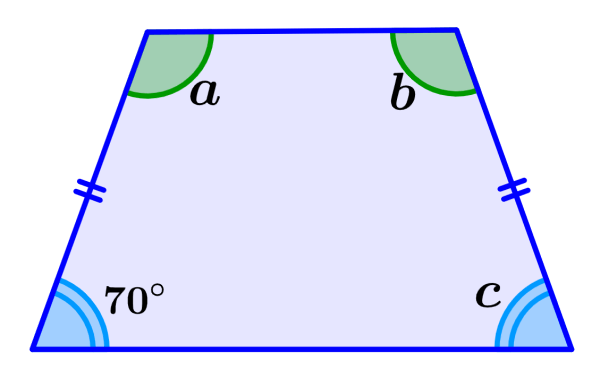
Solution: We solve this by following a process similar to the previous example. Therefore, we know that angle c measures 70°.
Now, we find the measures of the other two angles by adding the known angles and subtracting from 360°:
70°+70° = 140°
⇒ 360°-140° = 220°
The two missing angles have the same measure, so we divide the result by 2 and get 110°. This is the measure of angles a and b.
Calculate the interior angles of a scalene trapezoid
A scalene trapezoid is characterized by having all its sides of different lengths. This also means that all the internal angles of a scalene trapezoid are different from each other.
Therefore, to calculate the measure of an internal angle, we have to know the measures of the other three angles. We can also use the property that the adjacent interior angles of a trapezoid add up to 180°.
EXAMPLE
Find the measure of the missing angle in the scalene trapezoid below.
Solution: To find the missing angle, we have to add all the known angles and subtract the result from 360°. Therefore, we have:
100°+80°+70° = 250°
⇒ 360°-250° = 110°
The measure of the missing angle is 110°. We can see that the adjacent angles add up to 180°. That is, we have 100°+80° = 180° and we also have 110°+70° = 180°.
Calculate the interior angles of a right trapezoid
A right trapezoid has the main characteristic of having a pair of right angles, that is, a pair of 90° angles. One pair of sides of the trapezoid is parallel, so when we have a right angle, the angle of the other base must also be right.
We can find the measure of one angle in a right trapezoid if we know the measure of the other, different angles of the pair of right angles.
EXAMPLE
What is the measure of angle a in the following right trapezoid?
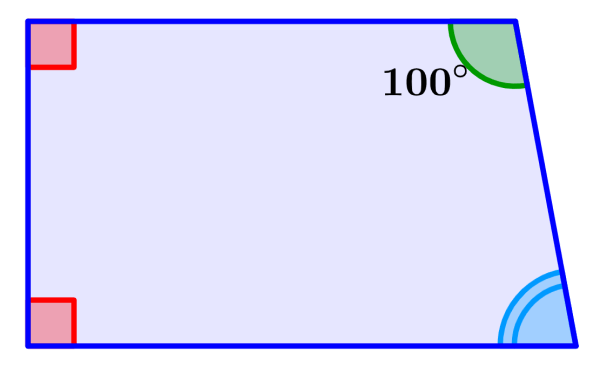
Solution: We know that the angles represented by a small triangle are the right angles, that is, they are equal to 90°. Therefore, we find the missing angle measure by adding all of the known angle measures and subtracting from 360°. Therefore, we have:
90°+90°+100° = 280°
Therefore, the missing angle measures 80°.
See also
Interested in learning more about the interior angles of a polygon? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
