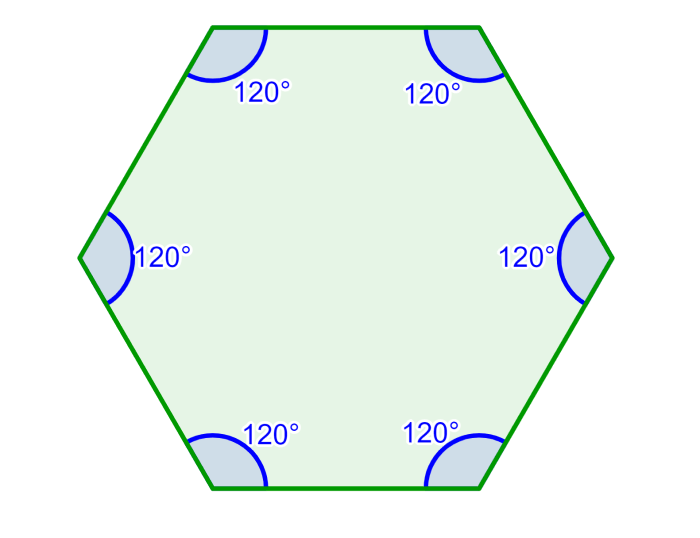
Hexagons have a sum of interior angles of 720°. A regular hexagon has all its angles with the same measure, so each interior angle measures 120°. On the other hand, irregular hexagons have angles with different measures, but they always have a total sum equal to 720°.
Here, we will learn about the interior angles of hexagons in more detail. We will learn the formula used to find the sum of these angles and we will look at some examples.
Sum of interior angles of a hexagon
The sum of all the interior angles of a hexagon is always equal to 720°. This is true regardless of whether the hexagon is regular or irregular. The sum of angles is obtained using the formula for the sum of polygons angles:
| $latex (n-2)\times 180$° |
where, n is the number of sides of the polygon. For a hexagon, we use $latex n = 6$. Therefore, we have:
$latex (n-2)\times 180$°
$latex =(6-2)\times 180$°
$latex =(4)\times 180$°
$latex =720$°
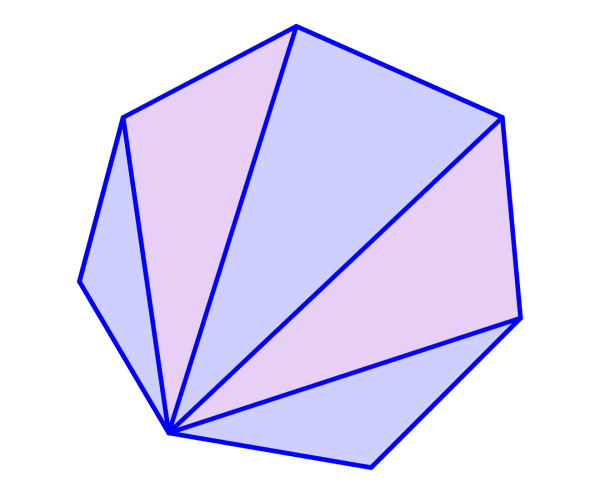
The formula for the sum of interior angles can be obtained when we divide any polygon into triangles as in the following diagram:
We know that the sum of interior angles of any triangle is equal to 180°. Furthermore, we can form a total of n-2 triangles in any polygon, where, n is the number of sides of the polygon. This means that $latex (n-2) \times 180$° corresponds to the sum of all the interior angles of the polygon.
How to determine the measures of all interior angles of hexagons?
When we have a regular hexagon, we can determine the measures of each interior angle by dividing the total sum of angles by 6. This is possible because all interior angles in a regular polygon have the same measure. Therefore, we have:
720°÷6 = 120°
Each interior angle in a regular hexagon has a measure equal to 120°.
To determine the measures of any missing angle in irregular hexagons, we need to know the measures of the other angles since these hexagons have internal angles that are different from each other.
For example, if we have a hexagon with interior angles 100°, 110°, 120°, 130°, 150°, we can determine the measure of the sixth angle by adding the known angles and subtracting from 720°:
100°+110°+120°+130°+150° = 610°
⇒ 720°-610° = 110°
The measure of the missing angle is 110°.
Solved examples of interior angles of a hexagon
EXAMPLE 1
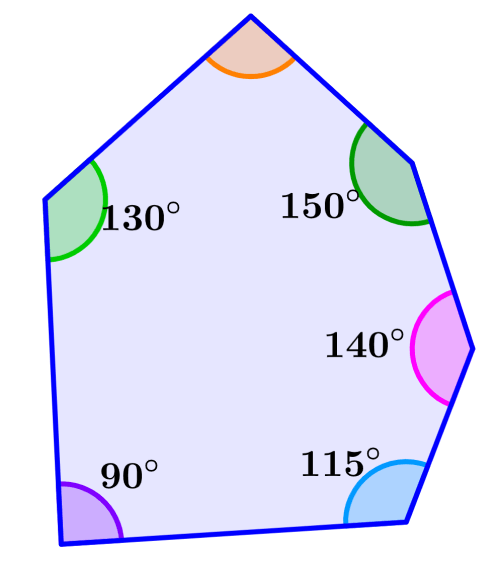
Determine the missing angle in the hexagon below.
Solution: We can look at the angles 130°, 90°, 115°, 140°, and 150°. Therefore, we start by adding them:
130°+90°+115°+140°+150° = 625°
Now, we subtract the obtained value from 720° to find the missing angle:
720°-615° = 95°
The missing angle measures 95°.
EXAMPLE 2
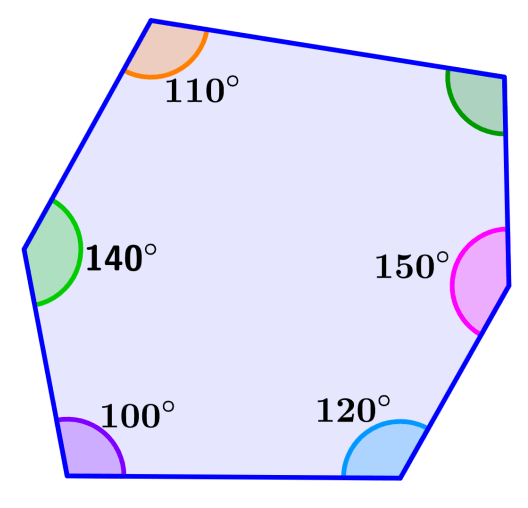
Find the missing angles in the hexagon below.
Solution: We have the measures of five of the six interior angles of the irregular hexagon. We know that the total sum equals 720°, so we can add the known angles and subtract from 720°:
110°+140°+100°+120°+150° = 620°
⇒ 720°-620° = 100°
The measure of the missing angle is 100°.
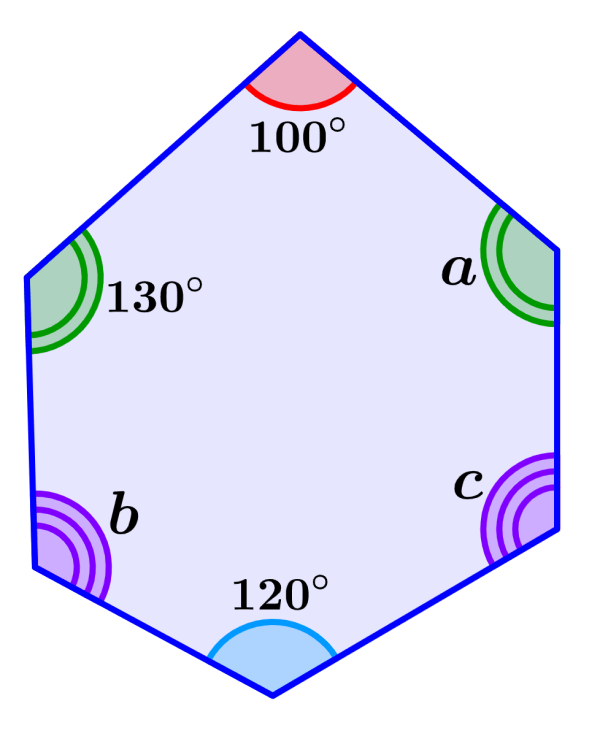
EXAMPLE 3
In the following example, we have to find more than one missing angle. In this case, the angles that are different have different symbols. For example, angles that have a double line are equal.
Solution: We know that the angles that have a double line are equal, therefore we have a=130°.
Similarly, angles b and c are equal since they have triple lines. We can find the measure of these angles by following a process similar to the previous example. We start by adding the known angles:
100°+130°+130°+120° = 480°
Now, we have to subtract this value from 480° to find the missing angles:
720°-480° = 240°
The missing angles have the same measure, so we divide the obtained value by 2 to obtain the value of each angle. Therefore, we have b=120° and c=120°.
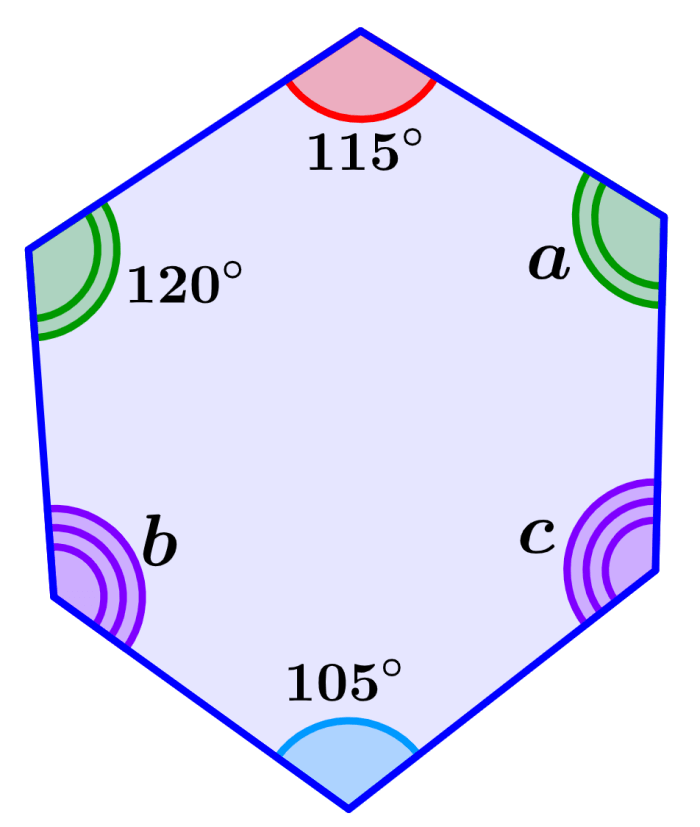
EXAMPLE 4
Find the missing angles in the hexagon below.
Solution: The angles shared by the three lines are equal. Therefore, we have a=120°.
Angles b and c also have the same measure since they are both represented by a double line. We can determine its measure by starting by adding the angles we know:
115°+120°+120°+105°=460°
Now, we subtract the obtained value from 720° and we have:
720°-460° = 260°
The result represents the sum of the two missing angles. Since both angles are equal, we have to divide by 2 to get the value of one angle. Therefore, we have b = 130° and c = 130°.
See also
Interested in learning more about the interior angles of a polygon? Take a look at these pages: