The height of a triangle is the perpendicular distance from the base to the opposite vertex. We can calculate the height of a scalene triangle using different formulas depending on the information we have available. For example, we can calculate the height if we know the lengths of all the sides. Additionally, we can use the length of a side and an adjacent angle or we can also use the area and the length of the base.
Here, we will learn about the different formulas that we can use to find the height of a scalene triangle. In addition, we will look at some problems in which we will apply these formulas to obtain the answer.
Formulas for the height of a scalene triangle
Depending on the information we have available, we can use two different formulas to find the height of a scalene triangle.
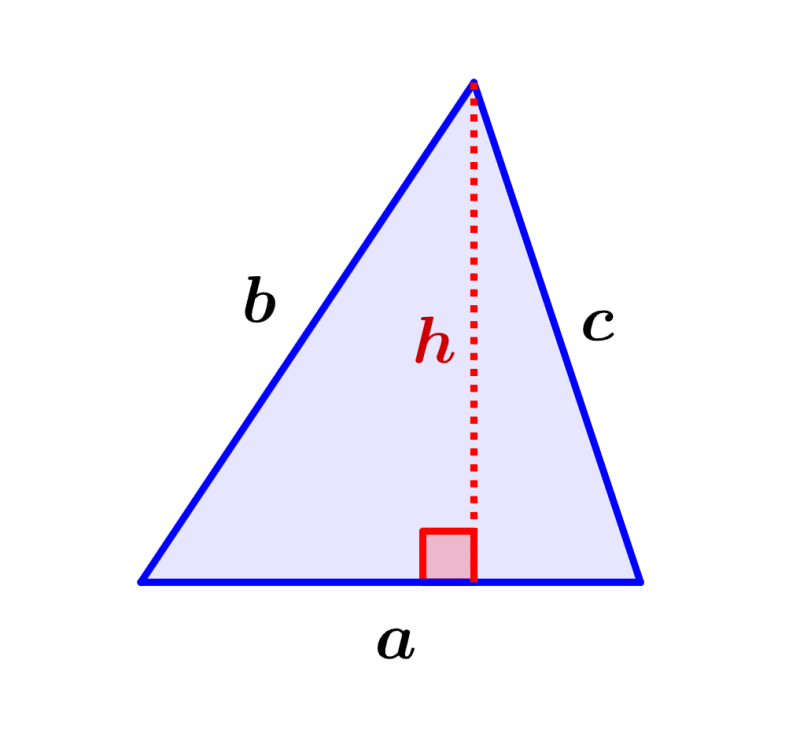
Height of a scalene triangle if we know all its sides
When we know the lengths of all the sides of the triangle, we can calculate the height using a formula that is derived from Heron’s formula, which is used to calculate the area:
| $latex h=\frac{2}{a}\sqrt{S(S-a)(S-b)(S-c)}$ |
where,
- $latex a, ~b, ~c$ are the lengths of the sides of the triangle
- $latex S$ is the semiperimeter, which is equal to $latex S=\frac{a+b+c}{2}$
- $latex h$ is the height perpendicular to the base
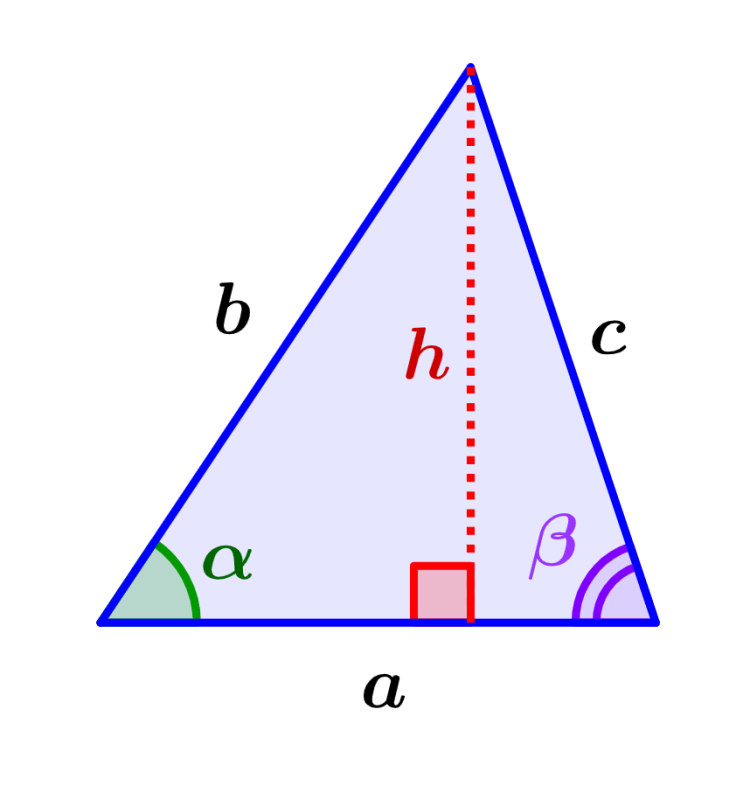
Height of a scalene triangle if we know a side and its angle or the area and its base
If we know the length of one of its sides and the measure of one of its angles or if we know its area and the length of its base, we can use the following formulas:
| $latex h=b\cdot\sin(\alpha)$ $latex h=c\cdot\sin(\beta)$ $latex h=\frac{2A}{a}$ |
where,
- $latex b,~c$ are the lengths of the lateral sides
- $latex a$ is the length of the base
- $latex \alpha,~\beta$ are the measures of the angles at the base
- $latex A$ is the area of the triangle
- $latex h$ is the height perpendicular to the base
Height of a scalene triangle – Examples with answers
The formulas for the height of a scalene triangle indicated above are applied to solve the following examples. Each example has its respective solution, but it is recommended that you try to solve the problems yourself before looking at the answer.
EXAMPLE 1
A scalene triangle has sides of lengths 6 m, 8 m, and 10 m, where the base is 6 m. What is the length of its height?
Solution
We can use the first formula with the following data:
- Side 1 and base, $latex a=6$m
- Side 2, $latex b=8$m
- Side 3, $latex c=10$m
We substitute these values in the formula:
$latex h=\frac{2}{a}\sqrt{S(S-a)(S-b)(S-c)}$
To find S, we use the formula:
$latex S=\frac{a+b+c}{2}$
$latex S=\frac{6+8+10}{2}$
$latex S=\frac{24}{2}$
$latex S=12$
Using these values, we have:
$latex h=\frac{2}{a}\sqrt{S(S-a)(S-b)(S-c)}$
$latex h=\frac{2}{6}\sqrt{12(12-6)(12-8)(12-10)}$
$latex h=\frac{2}{6}\sqrt{12(6)(4)(2)}$
$latex h=\frac{2}{6}\sqrt{576}$
$latex h=\frac{2}{6}(24)$
$latex h=8$
The height is 8 m.
EXAMPLE 2
A scalene triangle has sides of lengths 12 m, 14 m, and 16 m, and the base is 14 m. What is the length of its height?
Solution
We have the following information:
- Side 1, $latex a=12$m
- Side 2 y base, $latex b=14$m
- Side 3, $latex c=16$m
We substitute these values in the formula:
$latex h=\frac{2}{b}\sqrt{S(S-a)(S-b)(S-c)}$
We start by finding S:
$latex S=\frac{a+b+c}{2}$
$latex S=\frac{12+14+16}{2}$
$latex S=\frac{42}{2}$
$latex S=21$
Using these values, we have:
$latex h=\frac{2}{a}\sqrt{S(S-a)(S-b)(S-c)}$
$$h=\frac{2}{14}\sqrt{21(21-12)(21-14)(21-16)}$$
$latex h=\frac{2}{14}\sqrt{21(9)(7)(5)}$
$latex h=\frac{2}{14}\sqrt{6615}$
$latex h=\frac{2}{14}(81.33)$
$latex h=11.62$
The height is 11.62 m.
EXAMPLE 3
What is the length of the height of a triangle if its lateral side is 16 m and its angle at the base is 30°?
Solution
We can use the following formula:
$latex h=b\cdot \sin(\alpha)$
where, $latex b=16$ m and $latex \alpha=30$°. Therefore, we have:
$latex h=b\cdot \sin(\alpha)$
$latex h=16\cdot \sin(30)$
$latex h=16(0.5)$
$latex h=8$
The length of the height is 8 m.
EXAMPLE 4
What is the length of the height of a triangle if its lateral side is 22 m and its angle at the base is 60°?
Solution
We use the following formula:
$latex h=b\cdot \sin(\alpha)$
where, $latex b=22$ m and $latex \alpha=60$°. Therefore, we have:
$latex h=b\cdot \sin(\alpha)$
$latex h=22\cdot \sin(60)$
$latex h=22(0.866)$
$latex h=19.05$
The length of the height is 19.05 m.
EXAMPLE 5
What is the height of a scalene triangle that has an area of 100 m² and a base of 25 m?
Solution
We can use the formula:
$latex h= \frac{2A}{b}$
where, $latex b=25$ m and $latex A=100$ m². Therefore, we have:
$latex h= \frac{2A}{b}$
$latex h= \frac{2(100)}{25}$
$latex h= 8$
The height is 8 m.
Height of a scalene triangle – Practice problems
Use the formulas for the height of a scalene triangle to solve the following problems. If you need help with this, you can look at the solved examples above.
See also
Interested in learning more about scalene triangles? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
