The diameter of a sphere is equal to the line segment connecting two ends of the sphere and passing through the center. Diameter is an important measure of the sphere since, similar to the radius, we can also use the diameter to calculate the volume and surface area of the sphere. This means that it is also possible to find the length of the diameter if we know the volume or the surface area of the sphere.
Here, we will learn about three different methods that we can use to find the length of the diameter. In addition, we will use these methods to solve some problems.
Diameter of a sphere using the radius
The radius of a sphere is the line segment that connects the center of the sphere to any point on its surface. The radius is probably the most important dimension of a sphere.
This means that in most cases, we will know the length of the radius. We can calculate the length of the diameter starting from the radius simply by multiplying the radius by 2. Therefore, if we have the length of the radius, we use the following expression to get the length of the diameter:
$latex d=2r$
EXAMPLE 1
If a sphere has a radius of 5 m, what is its diameter?
Solution: We have the length $latex r=5$. Therefore, we use the formula with this value:
$latex d=2r$
$latex d=2(5)$
$latex d=10$
The diameter is 10 m.
EXAMPLE 2
What is the diameter of a sphere that has a radius of 11 m?
Solution: We use the value $latex r=11$ in the given formula:
$latex d=2r$
$latex d=2(11)$
$latex d=22$
The diameter measures 22 m.
Diameter of a sphere using the volume
The diameter of a sphere can be calculated if we have its volume. Recall that the following is the formula for the volume of a sphere:
$latex V=\frac{4}{3}\pi {{r}^3}$
Writing this in terms of the diameter, we have:
$latex V=\frac{1}{6}\pi {{d}^3}$
Therefore, we use this formula and solve for d.
EXAMPLE 1
If a sphere has a volume of 100 m³, what is its diameter?
Solution: We use the value $latex V=100$ in the volume formula and solve for d:
$latex V=\frac{1}{6}\pi {{d}^3}$
$latex 100=\frac{1}{6}\pi {{d}^3}$
$latex {{d}^3}=\frac{6(100)}{\pi}$
$latex {{d}^3}=\frac{600}{\pi}$
$latex {{d}^3}=191$
$latex d \approx 5.76$
The diameter measures 5.76 m.
EXAMPLE 2
What is the diameter of a sphere that has a volume of 240 m³?
Solution: We substitute the value $latex V=240$ in the volume formula and solve for d:
$latex V=\frac{1}{6}\pi {{d}^3}$
$latex 240=\frac{1}{6}\pi {{d}^3}$
$latex {{d}^3}=\frac{6(240)}{\pi}$
$latex {{d}^3}=\frac{1440}{\pi}$
$latex {{d}^3}=458.4$
$latex d \approx 7.71$
The diameter measures 7.71 m.
Diameter of a sphere using the surface area
We can also use the surface area to calculate the diameter of a sphere. For this, we use the formula for surface area and solve for the diameter. Recall that the formula for the surface area of a sphere is:
$latex A_{s}=4\pi {{r}^2}$
Writing in terms of the diameter, we have:
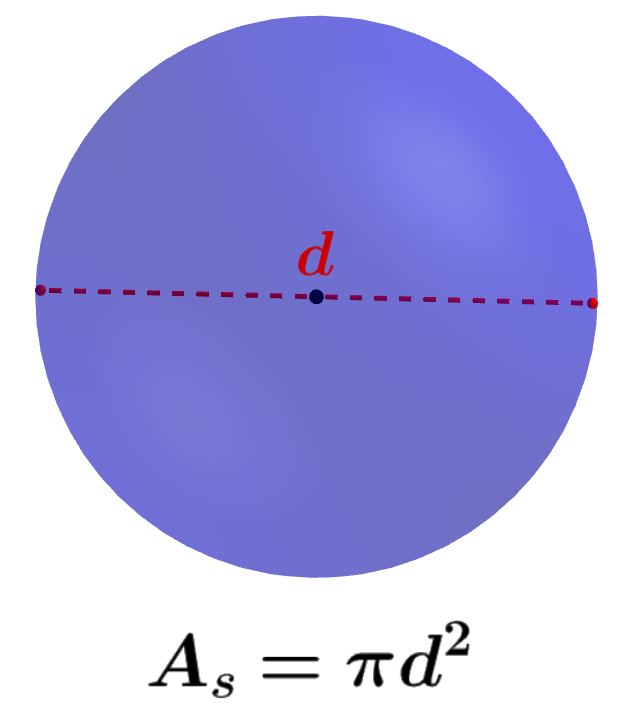
$latex A_{s}=\pi {{d}^2}$
EXAMPLE 1
What is the diameter of a sphere that has a surface area of 100 m²?
Solution: We use the value $latex A_{s}=100$ in the formula for surface area and solve for d:
$latex A_{s}=\pi {{d}^2}$
$latex 100=\pi {{d}^2}$
$latex {{d}^2}=\frac{100}{\pi}$
$latex {{d}^2}=31.83$
$latex d\approx 5.64$
The diameter of the sphere measures 5.64 m.
EXAMPLE 2
If a sphere has a surface area of 240 m², what is its diameter?
Solution: We have the value $latex A_{s}=240$, so we use it in the formula for surface area and solve for d:
$latex A_{s}=\pi {{d}^2}$
$latex 240=\pi {{d}^2}$
$latex {{d}^2}=\frac{240}{\pi}$
$latex {{d}^2}=76.4$
$latex d\approx 8.74$
The diameter of the sphere measures 8.74 m.
See also
Interested in learning more about spheres? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
