The cross-section represents the intersection of a plane with a three-dimensional object. The cross-section is the two-dimensional figure obtained by the intersection of a plane with a three-dimensional figure. For example, when a cylinder is cut by a plane that is parallel to one of its bases, the cross-section obtained is a circle. Depending on the orientation of the plane, we can obtain several cross-sections from the same object.
Here, we will learn more details about the cross-sections and we will explore the cross-sections of the most important figures.
Types of cross sections
Depending on the orientation of the plane that cuts the object, we can have three types of cross-sections:
- Horizontal cross section
- Vertical cross section
- Inclined cross section
Horizontal or parallel cross-section
This cross-section is formed when a plane intersects an object in a direction parallel to the base of the object.
Vertical or perpendicular cross-section
A vertical cross-section is formed when an object is cut by a plane perpendicular to its base, that is, at an angle of 90°.
Inclined cross-section
This cross-section is formed when the angle of inclination of the plane that intersects the object is greater than 0° and less than 90°.
Cross-section area
When a plane intersects a solid object, an area is projected onto the plane. If the plane is oriented horizontally, it will be perpendicular to the axis of symmetry. Depending on the figure, we can calculate the cross-sectional area by recognizing that the cross-section equals the bases of the figure.
EXAMPLE
Find the cross-sectional area of a plane parallel to the base of a cube that has a volume equal to 125 m³.
Solution: We can recognize that the cross-sectional area will be equal to the area of one of the faces of the cube since the plane is parallel to the bases. Therefore, we have to find the area of one face of the cube.
The volume of the cube is equal to $latex V = {{a}^3}$, where, a is the length of one side of the cube. This means that the length of one side is $latex a = 5$.
Now, we know that the area of a square is $latex A = {{a}^2}$, so the cross-sectional area is $latex A=25$.
Cross-sections of a cube
A cube is a three-dimensional figure that has all its sides of the same length. A cube has a total of six square faces. This means that when a plane intersects a cube in a direction that is parallel to one of its faces, the cross-section will always be a square.
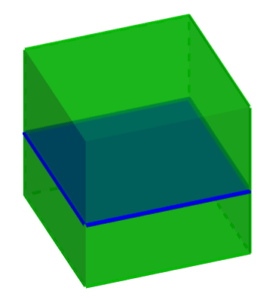
However, it is also possible to obtain different cross-sections by cutting the cube with an inclination relative to its base. If the plane intersects three edges of the cube, its cross-section will be a triangle.
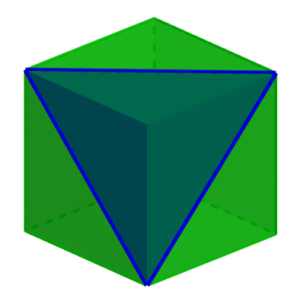
If the cutting plane cuts the cube in a way that crosses the diagonals of the faces, we will obtain a rectangular cross-section:
Additionally, we can also form a hexagonal cross-section by intersecting the cube with an inclined plane as follows:
Cross-sections of a cylinder
A cylinder is a 3D figure that has circular bases, which are connected by a lateral surface. Depending on how it is cut, the cross-sections of the cylinder can be a circle, a rectangle, or an oval. If the cylinder is cut with a plane parallel to one of its bases, the cross-section will be a circle.
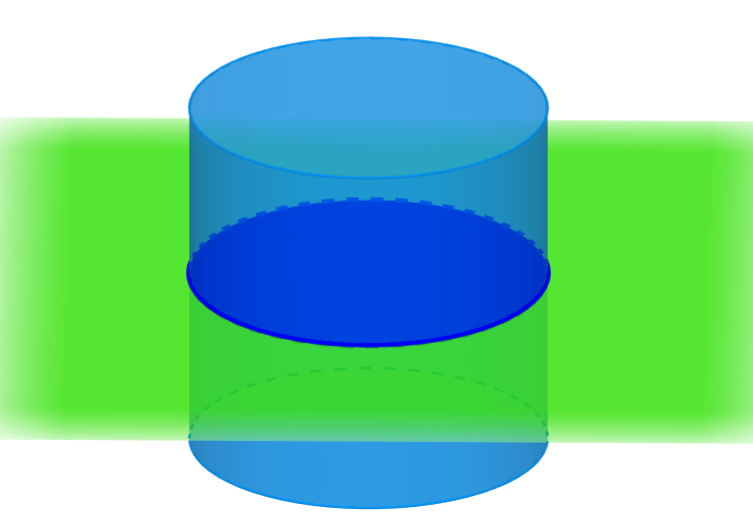
The oval cross-section is obtained when the plane intersects the cylinder with an angle greater than 0° and less than 90° with respect to the base.
If the plane cuts the cylinder in a direction perpendicular to the bases, the cross-section will be a rectangle.
Cross-sections of a cone
A cone can be considered as a pyramid with a circular cross-section. Depending on the relationship between the plane and the cut surface, the cross-sections of a cone can be circles, ellipses, parabolas, and hyperbolas.
A circle is formed when a cone is cut by a plane that is parallel to its base.
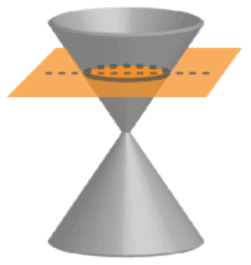
An ellipse is formed when a cone is cut by a plane that is inclined at a small angle (less than the angle of the lateral sides) with respect to the base of the cone.
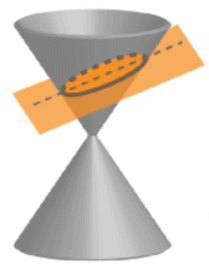
A parabola is formed when the plane that intersects the cone is parallel to one lateral side of the cone.
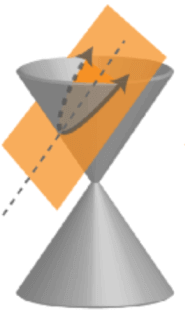
A hyperbola is formed when the plane that intersects the cone has a superior angle (greater than the angle of the lateral sides) with respect to the base of the cone.
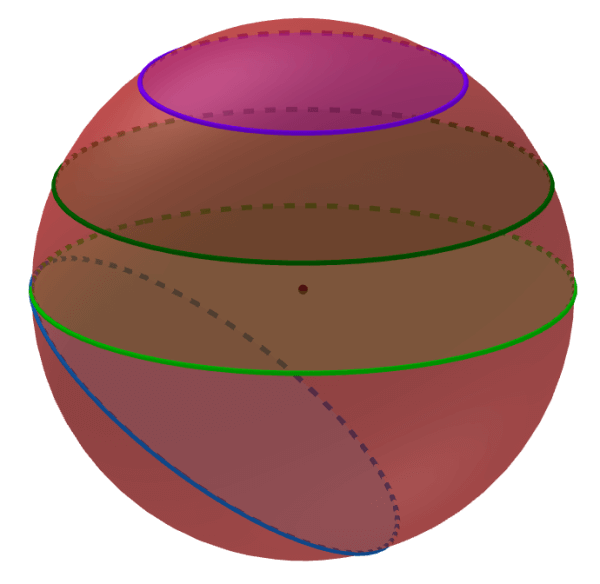
Cross-sections of a sphere
A sphere is a perfectly round three-dimensional figure. The cross-section of a sphere is always a circle regardless of the orientation of the plane.
See also
Interested in learning more about geometric figures? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
