The volume of geometric figures is one of the most important measurements of three-dimensional figures. Volume is a measure of the space occupied by an object in three-dimensional space. Since volume is a three-dimensional measure, we use cubic units to measure it. The volume formula depends on the shape of the figure and its different dimensions.
Here, we will learn about the formulas of the most important three-dimensional figures. Then, we will use these formulas to solve some problems.
GEOMETRY
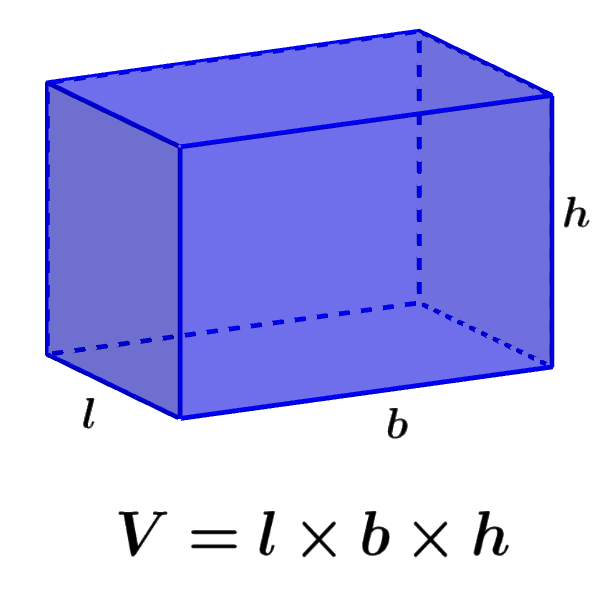
Relevant for…
Learning about the formulas for the volume of geometric figures.
GEOMETRY
Relevant for…
Learning about the formulas for the volume of geometric figures.
Definition of volume
The volume of a geometric figure is defined as the amount of space occupied by the object or figure in three-dimensional space. Volume is measured in cubic units, for example, m³, cm³, and so on. Volume can be considered as the capacity of a container to hold a quantity of fluid (gas or liquid).
Volume can be calculated using arithmetic by multiplying its various dimensions and, in certain cases, using some constants. Two geometric figures can have the same volume depending on their dimensions and shape.
Formulas for the volume of geometric figures
The formula for the volume of geometric figures depends on the shape and dimensions of the figure. There are a large number of three-dimensional geometric figures, however, the most important ones are the cube, the rectangular prism, the cylinder, the sphere, the pyramid, and the tetrahedron.
Volume of a rectangular prism
A rectangular prime is a prism with rectangular bases and with rectangular lateral faces. The volume of these prisms depends on their three dimensions.
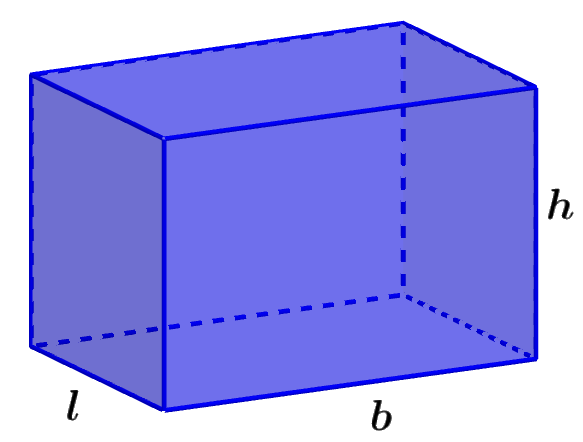
Volume of rectangular prism = lbh
where l is the length of the width of the prism and b is the length of the base and h is the length of the height.
Volume of a cube
A cube is a three-dimensional figure that has all its sides of the same length. A cube has a total of six square faces.
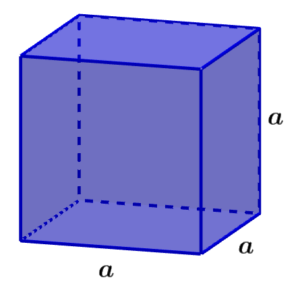
Volume of a cube = a³
where a is the length of one of the sides of the cube.
Volume of a cylinder
A cylinder is characterized by having two circular bases and a surface that joins the two bases.
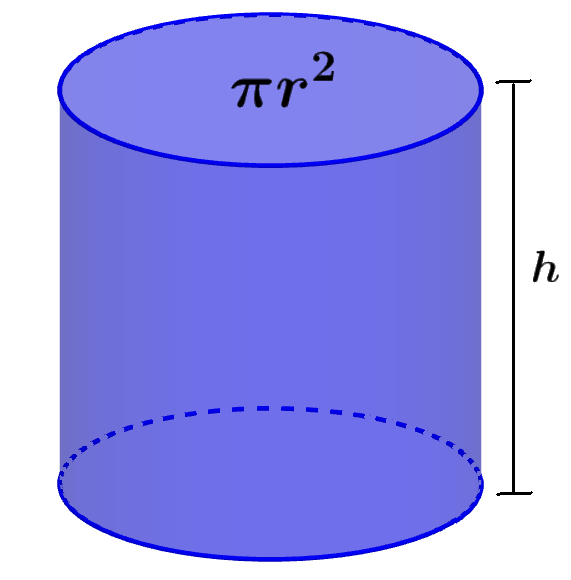
Volume of cylinder = πr²h
where r is the radius of the bases and h is the height of the cylinder.
Volume of a sphere
A sphere is a completely round three-dimensional figure. The sphere is defined by the radius.
Volume of sphere = (4⁄3)πr³
where r represents the radius of the sphere and π is a mathematical constant with a value of 3.1415…
Volume of a tetrahedron
A tetrahedron is a three-dimensional figure that has four triangular faces.
Volume of tetrahedron = $latex \frac{{{a}^3}}{6 \sqrt{2}}$
where a is the length of one of the sides of the tetrahedron.
Table of formulas for the volume of geometric figures
| Figure | Volume |
| Rectangular prism | V = lbh |
| Cube | V = a³ |
| Cylinder | V = πr²h |
| Prism | V = Bh |
| Sphere | V = (4⁄3)πr3 |
| Pyramid | V = (1⁄3) Bh |
| Circular Cone | V = (1⁄3)πr2h |
| Tetrahedron | V = $latex \frac{{{a}^3}}{6\sqrt{2}}$ |
where r is the radius, a and l represent the different lengths of the figures, h represents the height and B represents the area of the base.
Volume of geometric figures – Examples with answers
The formulas for the volume of three-dimensional figures are used to solve the following examples. Each exercise has its respective solution, where you can see the process used.
EXAMPLE 1
If a cube has sides of length 10 m, what is its volume?
Solution
The volume of a cube is found by cubing the length of one of its sides. Therefore, we have:
$latex V={{a}^3}$
$latex V={{10}^3}$
$latex V=1000$
Thus, the volume of the cube is 1000 m³.
EXAMPLE 2
A cylinder has bases with a radius of 5 m and a height of 6 m. What is its volume?
Solution
We can recognize the dimensions $latex r = 5$ and $latex h = 6$. Therefore, using the formula for the volume with these dimensions, we have:
$latex V=\pi {{r}^2}h$
$latex V=\pi {{(5)}^2}(6)$
$latex V=\pi (25)(6)$
$latex V=471.2$
Thus, the volume of the cylinder is 471.2 m³.
EXAMPLE 3
What is the volume of a sphere that has a radius of 8 m?
Solution
We use the formula for the volume of the sphere with the given radius. Therefore, we have:
$latex V=\frac{4}{3}\pi {{r}^3}$
$latex V=\frac{4}{3}\pi {{(8)}^3}$
$latex V=2144.7$
Thus, the volume of the sphere is 2144.7 m³.
EXAMPLE 4
What is the volume of a tetrahedron that has sides of length 5 m?
Solution
We use the given length in the formula for the volume of a tetrahedron:
$latex V=\frac{{{a}^3}}{6\sqrt{2}}$
$latex V=\frac{{{5}^3}}{6\sqrt{2}}$
$latex V=\frac{125}{6\sqrt{2}}$
$latex V=14.7$
The volume of the tetrahedron is 14.7 m³.
Volume of geometric figures – Practice problems
Apply the formulas for the volume of three-dimensional figures to solve the following practice problems. Select an answer and click “Check” to verify that you got the correct answer.
See also
Interested in learning more about geometric figures? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
