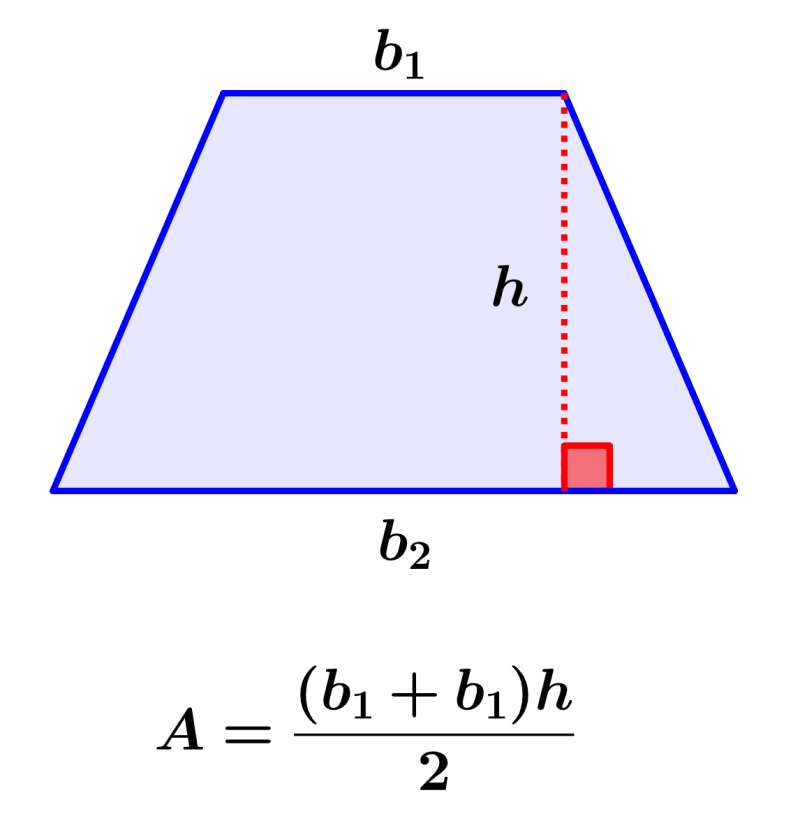
The area of a trapezoid can be considered as the region covered by the trapezoid in a two-dimensional plane. A trapezoid is a 2D figure that falls within the category of quadrilaterals. In a trapezoid, one pair of sides is parallel and the other pair of sides is not parallel. Similar to other geometric figures, the trapezoid also has its own properties and formulas based on area and perimeter.
Here, we will learn about the formula for the area of a trapezoid. In addition, we will look at some exercises in which we will apply this formula to find the area.
Formula for the area of a trapezoid
To find the area of a trapezoid, we calculate the sum of its bases, multiply that sum by the height of the trapezoid, and then divide the result by 2. The formula for the area of the trapezoid is:
| $latex A=\frac{(b_{1}+b_{2})h}{2}$ |
where,
- $latex b_{1}=$ the length of the base 1 of the trapezoid
- $latex b_{2}=$ the length of the base 2 of the trapezoid
- $latex h=$ the length of the height of the trapezoid
Each base of the trapezoid should be perpendicular to the height. In the figure, we can see that both bases are sides of the trapezoid. However, since the lateral sides are not perpendicular to either base, a broken line is drawn to represent the height.
Derivation of the formula for the area of a trapezoid
Let’s use the following figure to derive the formula for the area of a trapezoid:
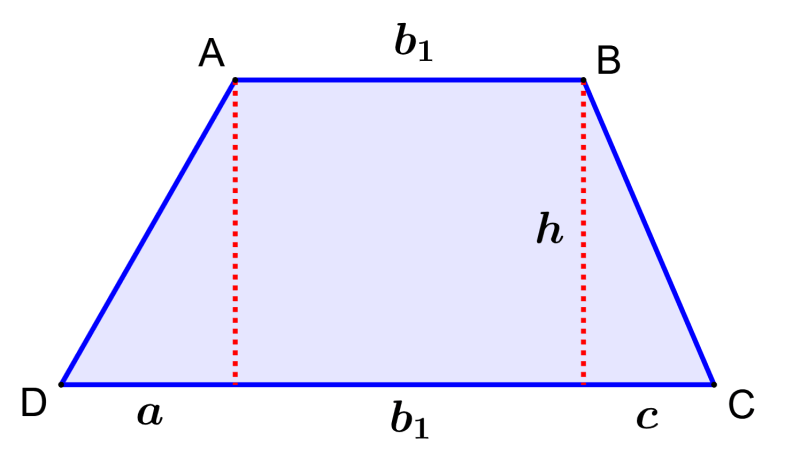
The area of a trapezoid is equal to the sum of the areas of the two triangles and the area of the rectangle. Thus, we know that:
trapezoid area = triangle area 1 + rectangle area + triangle area 2
$latex A=\frac{ah}{2}+b_{1}h+\frac{ch}{2}$
$latex A=\frac{ah+2b_{1}h+ch}{2}$
We can simplify the expression and rearrange the terms to get:
$latex A=\frac{h}{2}(b_{1}+(a+b_{1}+c))$
If we use $latex b_{2}$ to represent the longest base of the trapezoid, we have:
$latex b_{2}=a+b_{1}+c$
Substituting this in the previous equation, we have:
$latex A=\frac{h}{2}(b_{1}+b_{2})$
Therefore, the area of the trapezoid with bases $latex b_{1}, ~b_{2}$ and height $latex h$ is $latex A=\frac{h}{2}(b_{1}+b_{2})$.
Area of a trapezoid – Examples with answers
The following examples can be used to practice applying the formula for the area of a trapezoid. Try to solve the examples yourself before looking at the result.
EXAMPLE 1
Find the area of a trapezoid that has bases of length 8 m and 12 m and a height of 10 m.
Solution
We have the following information:
- Base 1, $latex b_{1}=8$ m
- Base 2, $latex b_{2}=12$ m
- Height, $latex h=10$ m
Thus, we use the area formula by replacing the given values:
$latex A=\frac{(b_{1}+b_{2})h}{2}$
$latex =\frac{(8+12)10}{2}$
$latex =\frac{(20)(10)}{2}$
$latex =\frac{200}{2}$
$latex A=100$
The area of the trapezoid is 100 m².
EXAMPLE 2
What is the area of a trapezoid that has bases of length 11 m and 15 m and height 12 m?
Solution
The question gives us the following information:
- Base 1, $latex b_{1}=11$ m
- Base 2, $latex b_{2}=15$ m
- Height, $latex h=12$ m
Using the given information, we have:
$latex A=\frac{(b_{1}+b_{2})h}{2}$
$latex =\frac{(11+15)12}{2}$
$latex =\frac{(26)(12)}{2}$
$latex =\frac{312}{2}$
$latex A=156$
The area of the trapezoid is 156 m².
EXAMPLE 3
A trapezoid has an area of 200 cm², a base of length 9 cm, and the other base of length 11 cm. What is the height of the trapezoid?
Solution
We have the following information:
- Area, $latex A=200$ cm²
- Base 1, $latex b_{1}=9$ cm
- Base 2, $latex b_{2}=11$ cm
To find the height, we use the area formula and solve for h:
$latex A=\frac{(b_{1}+b_{2})h}{2}$
$latex 200=\frac{(9+11)h}{2}$
$latex 400=(9+11)h$
$latex 400=20h$
$latex h=20$
The height of the trapezoid is 20 cm.
EXAMPLE 4
A trapezoid has an area of 240 m², a base of length 11 m, and the other base of length 13 m. What is the height of the trapezoid?
Solution
From the question, we can get the following values:
- Area, $latex A=240$ m²
- Base 1, $latex b_{1}=11$ m
- Base 2, $latex b_{2}=13$ m
We use the formula with the given values and solve for h:
$latex A=\frac{(b_{1}+b_{2})h}{2}$
$latex 240=\frac{(11+13)h}{2}$
$latex 480=(11+13)h$
$latex 480=24h$
$latex h=20$
The height of the trapezoid is 20 m.
EXAMPLE 5
Find the area of the following trapezoid:
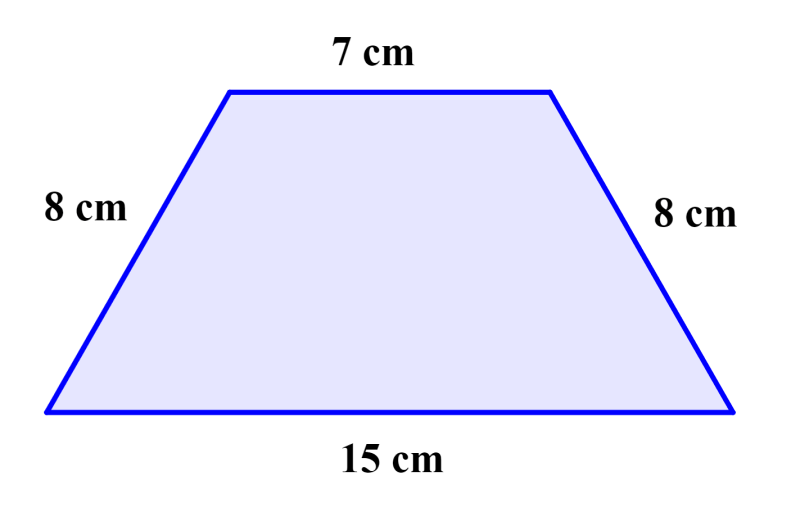
Solution
Since the non-parallel sides of the trapezoid are equal, the height can be calculated as follows:
We get the bases of the two triangles by subtracting 7 from 15 and dividing by 2.
⇒ $latex \frac{15-7}{2}=4$ cm
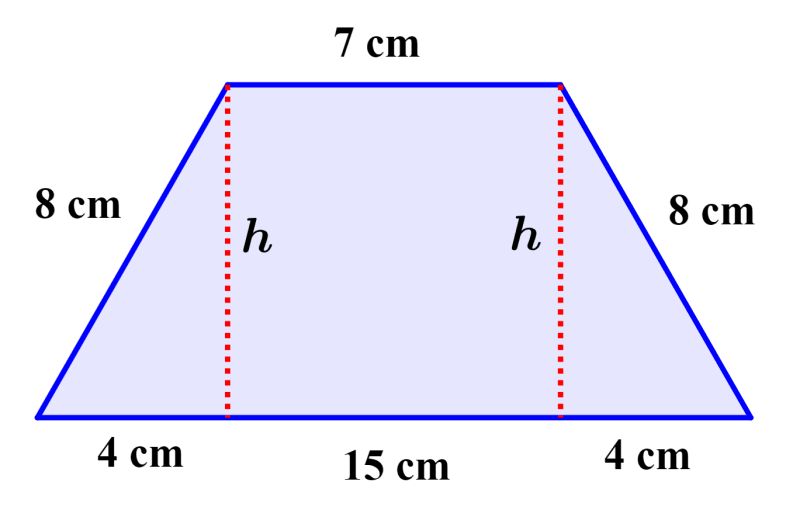
Now, we can use the Pythagorean Theorem to find the height. Therefore, we have:
$latex {{8}^2}={{h}^2}+{{4}^2}$
$latex 64={{h}^2}+16$
$latex {{h}^2}=48$
$latex h=6.93$ cm
The height of the trapezoid is 6.93 cm. Now, we calculate the area with these values:
$latex A=\frac{(b_{1}+b_{2})h}{2}$
$latex =\frac{(15+7)6.93}{2}$
$latex =\frac{(22)(6.93)}{2}$
$latex A=76.23$
The area of the trapezoid is 76.23 cm².
Area of a trapezoid – Practice problems
Put into practice what you have learned about the area of a trapezoid to solve the following problems. Select an answer and check it to make sure you selected the correct one.
See also
Interested in learning more about trapezoids? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
