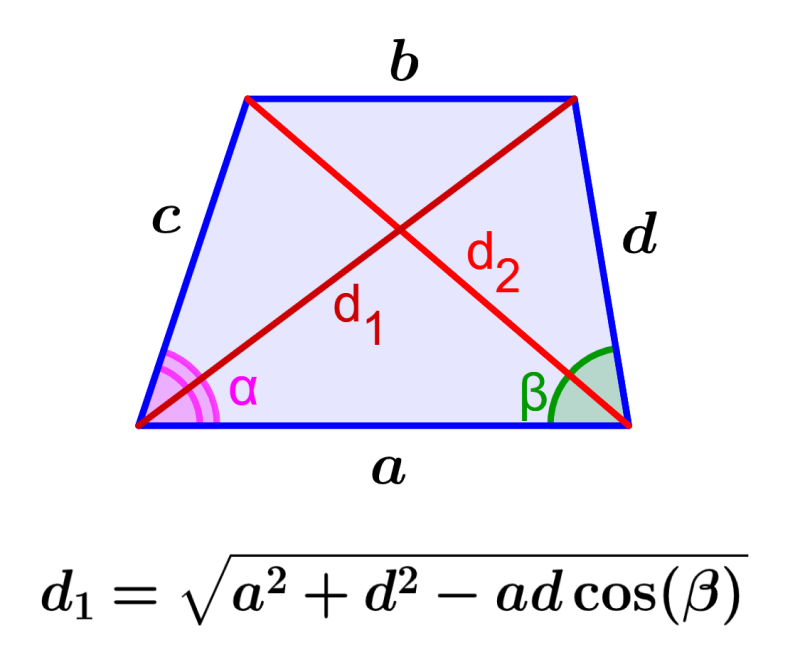
Recall that trapezoids are quadrilaterals that have a pair of sides that are parallel. The diagonals of the trapezoids connect to two opposite corners of the trapezoid. The lengths of these diagonals can be found using the law of cosines if we know the lengths of the sides and the angles of the bases. This can be done because the diagonals divide the trapezoid into two congruent triangles.
Here, we will learn about the formulas that we can use to find the lengths of both diagonals of a trapezoid. In addition, we will look at some examples where we will apply these formulas to obtain the answer.
Formula for the diagonal of a trapezoid
Suppose we have the following trapezoid:
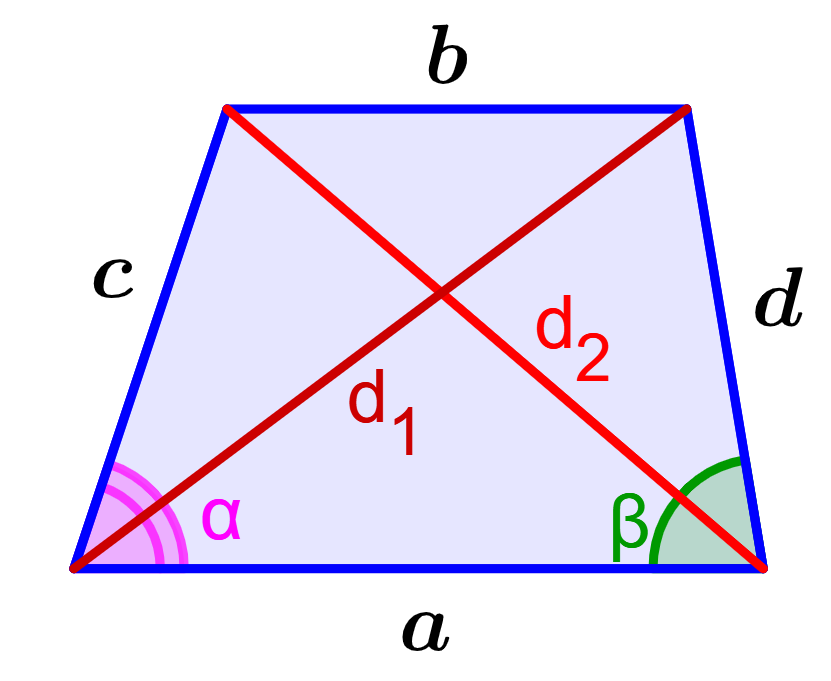
If we know the lengths of the sides and the angles of the bases, we can find the length of the diagonals of the trapezoid using the law of cosines:
$latex d_{1}=\sqrt{{{a}^2}+{{d}^2}-2ad~\cos(\beta)}$
$latex d_{2}=\sqrt{{{a}^2}+{{c}^2}-2ac~\cos(\alpha)}$
where,
- $latex a, ~b$ represent the lengths of the bases
- $latex b, ~c$ represent the lengths of the lateral sides
- $latex \alpha, ~\beta$ represent the angles of the bases
- $latex d_{1}, ~d_{2}$ represent the lengths of the diagonals
Diagonal of a trapezoid – Examples with answers
In the following examples, we apply the formulas detailed above to find the length of the diagonals of a trapezoid. Try to solve the examples yourself before looking at the solution.
EXAMPLE 1
We have that a trapezoid has sides of length 10 m and 12 m and the angle between them is 60°. What is the length of its diagonal?
Solution
We can use any definition for the sides of the trapezoid. The important thing when using the law of cosines is that the given angle is the angle that lies between the two given sides.
In this case, it is, so we can use the following definitions:
- Side 1, $latex a=10$ m
- Side 2, $latex d=12$ m
- Angle, $latex \beta= 60$°
And we replace these values in the formula:
$latex d_{1}=\sqrt{{{a}^2}+{{d}^2}-2ad~\cos(\beta)}$
$$d_{1}=\sqrt{{{10}^2}+{{12}^2}-2(10)(12)~\cos(60°)}$$
$latex d_{1}=\sqrt{100+144-240(0.5)}$
$latex d_{1}=\sqrt{244-120}$
$latex d_{1}=\sqrt{124}$
$latex d_{1}=11.14$
The length of the diagonal of the trapezoid is 11.14 m.
EXAMPLE 2
A trapezoid has sides of length 6 m and 8 m and the angle between them is 60°. What is the length of its diagonal?
Solution
We can recognize the following information:
Side 1, $latex a=6$ m
Side 2, $latex d=8$ m
Angle, $latex \beta=60$°
Now, we use the diagonal formula with these values:
$latex d_{1}=\sqrt{{{a}^2}+{{d}^2}-2ad~\cos(\beta)}$
$$d_{1}=\sqrt{{{6}^2}+{{8}^2}-2(6)(8)~\cos(60°)}$$
$latex d_{1}=\sqrt{36+64-96(0.5)}$
$latex d_{1}=\sqrt{100-48}$
$latex d_{1}=\sqrt{52}$
$latex d_{1}=7.2$
The length of the diagonal of the trapezoid is 7.2 m.
EXAMPLE 3
What is the length of the diagonal of a trapezoid that has sides with a length of 9 m and 15 m and the angle between those sides is 45°?
Solution
We can identify the following information:
Side 1, $latex a=9$ m
Side 2, $latex d=15$ m
Angle, $latex \beta=45$°
Now, we use the diagonal formula with these values:
$latex d_{1}=\sqrt{{{a}^2}+{{d}^2}-2ad~\cos(\beta)}$
$$d_{1}=\sqrt{{{9}^2}+{{15}^2}-2(9)(15)~\cos(45°)}$$
$latex d_{1}=\sqrt{81+225-270(0.707)}$
$latex d_{1}=\sqrt{306-190.89}$
$latex d_{1}=\sqrt{115.11}$
$latex d_{1}=10.73$
The length of the diagonal of the trapezoid is 10.73 m.
EXAMPLE 4
Determine the length of the diagonal of a trapezoid that has sides with a length of 20 m and 22 m and the angle between them is 30°.
Solution
We have the following data:
- Side 1, $latex a=20$ m
- Side 2, $latex d=22$ m
- Angle, $latex \beta =30$°
We use these values in the diagonal formula:
$latex d_{1}=\sqrt{{{a}^2}+{{d}^2}-2ad~\cos(\beta)}$
$$d_{1}=\sqrt{{{20}^2}+{{22}^2}-2(20)(22)~\cos(30°)}$$
$latex d_{1}=\sqrt{400+484-880(0.866)}$
$latex d_{1}=\sqrt{884-762.1}$
$latex d_{1}=\sqrt{121.9}$
$latex d_{1}=11.04$
The length of the diagonal of the trapezoid is 11.04 m.
Diagonal of a trapezoid – Practice problems
Put into practice what you have learned about the diagonals of a trapezoid and use the formulas to find the lengths of the diagonals. If you need help, you can look at the solved examples above.
See also
Interested in learning more about trapezoids? Take a look at these pages: