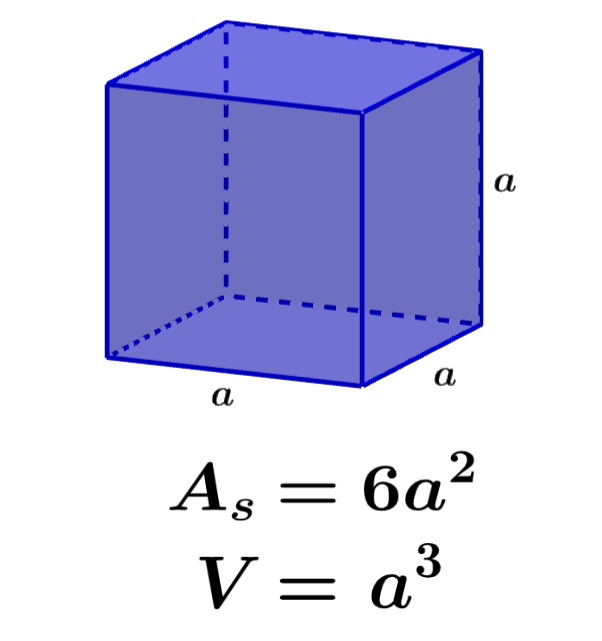
The surface area of a cube represents the sum of the areas of all the faces of the cube. On the other hand, volume is a measure of the three-dimensional space occupied by the cube. We can calculate the surface area of a cube using the formula A=6a² and we can calculate its volume using the formula V=a³, where a is the length of one of the sides of the cube.
In this article, we will learn all about the surface area and volume of a cube. We will explore their formulas and use them to solve some practice problems.
How to find the surface area of a cube?
We can calculate the surface area of a cube by adding the areas of its six faces. We know that the faces of a cube have a square shape. Therefore, we can calculate the area of each face of the cube by squaring the length of one of its faces.
Using the letter a to represent the length of one of the sides of the cube, we have:
$latex \text{Area of one face}={{a}^2}$
Adding the areas of the six faces of the cube, we have:
$latex A_{s}={{a}^2}+{{a}^2}+{{a}^2}+{{a}^2}+{{a}^2}+{{a}^2}$
| $latex A_{s}=6{{a}^2}$ |
where, $latex A_{s}$ represents the surface area and a represents the length of one of the sides of the cube.
How to find the volume of a cube?
Since all the sides of a cube have the same length, we can calculate its area by cubing the length of one of its sides. Therefore, we have the following:
Volume = Length × Width × Height
$latex V=a\times a \times a$
| $latex V={{a}^3}$ |
where, a is the length of one of the sides of the cube.
Calculate the volume of a cube using the diagonal
If we know the length of one of the diagonals of the cube instead of the length of its sides, we can use the following formula to calculate its volume:
| $latex V=\sqrt{3} \times \frac{{{d}^3}}{9}$ |
where d is the length of the diagonal of a cube.
Surface area and volume of cubes – Examples with answers
The formulas for the surface area and volume of a cube are used to solve the following examples. Each example has its solution, but try to solve the problems yourself before looking at the answer.
EXAMPLE 1
Find the surface area of a cube that has sides with a length of 5 inches.
Solution
We are going to use the surface area formula with the length $latex a=5$. Therefore, we have:
$latex A_{s}=6{{a}^2}$
$latex A_{s}=6{{(5)}^2}$
$latex A_{s}=6(25)$
$latex A_{s}=150$
The surface area is equal to 150 in².
EXAMPLE 2
Find the volume of a cube that has sides with a length of 5 feet.
Solution
Using the formula for the volume with the length of $latex a=5$, we have:
$latex V=a^3$
$latex V={{5}^3}$
$latex V=125$
The volume is equal to 125 ft³.
EXAMPLE 3
Find the surface area of a cube that has side lengths of 10 feet.
Solution
Using the length $latex a=10$ in the formula for the surface area, we have:
$latex A_{s}=6{{a}^2}$
$latex A_{s}=6{{(10)}^2}$
$latex A_{s}=6(100)$
$latex A_{s}=600$
The surface area is equal to 600 ft².
EXAMPLE 4
What is the volume of a cube that has sides with a length of 10 inches?
Solution
Using the formula for the volume with the length $latex a=10$, we have:
$latex V=a^3$
$latex V={{10}^3}$
$latex V=1000$
The volume is equal to 1000 in³.
EXAMPLE 5
Find the surface area of a cube that has sides with a length of 12 yards.
Solution
Using the length $latex a=12$ in the surface area formula, we have:
$latex A_{s}=6{{a}^2}$
$latex A_{s}=6{{(12)}^2}$
$latex A_{s}=6(144)$
$latex A_{s}=864$
The surface area is equal to 864 yd².
EXAMPLE 6
Find the length of the sides of a cube that has a volume of 512 in³.
Solution
In this case, we know the measure of the area, and we need to find the length of one of the sides. Therefore, we use the volume formula and solve for a:
$latex V=a^3$
$latex 512={{a}^3}$
$latex a=8$
The length of one of the sides is 8 in.
EXAMPLE 7
Find the length of the sides of a cube that has a surface area of 120 ft².
Solution
In this case, we know the surface area, and we need to find the length of its sides. Therefore, we use the surface area formula and solve for a:
$latex A_{s}=6{{a}^2}$
$latex 120=6{{a}^2}$
$latex 20={{a}^2}$
$latex a=4.47$
The length of the sides is equal to 4.47 ft.
EXAMPLE 8
If a cube has a diagonal of 5 inches, find its volume.
Solution
Here, we know the length of the diagonal $latex d=5$, so we can use the formula for the volume in terms of the diagonal with this value:
$latex V=\sqrt{3}\times \frac{{{d}^3}}{9}$
$latex V=\sqrt{3}\times \frac{{{5}^3}}{9}$
$latex V=\sqrt{3}\times \frac{125}{9}$
$latex V=24.1$
The volume is equal to 24.1 in³.
EXAMPLE 9
What is the length of the sides of a cube that has a surface area of 240 yd²?
Solution
We can use the surface area formula with $latex A_{s}=240$ and solve for a:
$latex A_{s}=6{{a}^2}$
$latex 240=6{{a}^2}$
$latex 40={{a}^2}$
$latex a=6.32$
The length of the sides is equal to 6.32 yd.
EXAMPLE 10
Find the volume of a cube that has a diagonal of 10 feet.
Solution
Using the length $latex d=10$ in the formula for volume in terms of the diagonal, we have:
$latex V=\sqrt{3}\times \frac{{{d}^3}}{9}$
$latex V=\sqrt{3}\times \frac{{{10}^3}}{9}$
$latex V=\sqrt{3}\times \frac{1000}{9}$
$latex V=192.5$
The volume is equal to 192.5 ft³.
Surface area and volume of a cube – Practice problems
Use the following problems to practice using the formulas for surface area and volume of cubes. You can use the solved examples above as a guide.
See also
Interested in learning more about the area and volume of geometric figures? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
