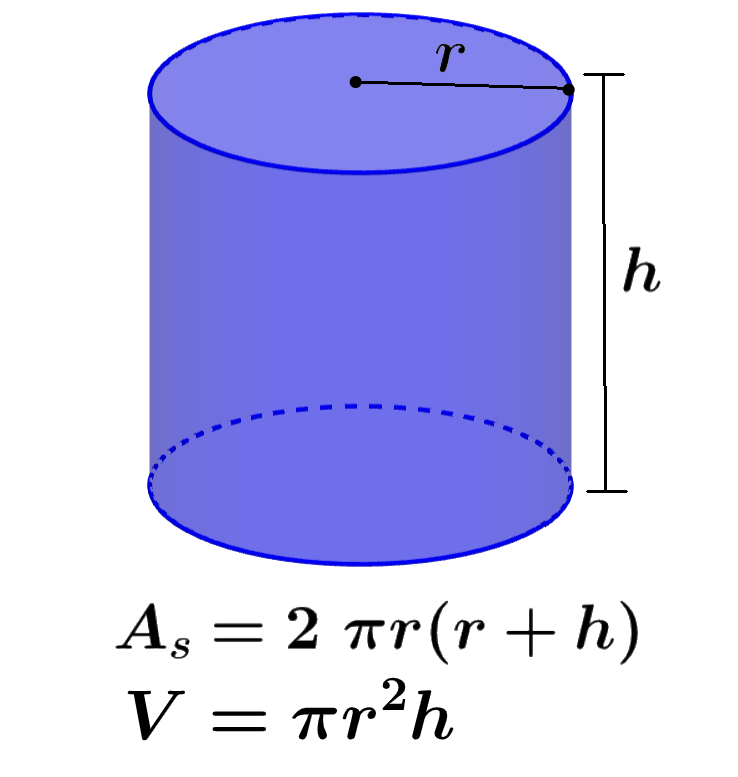
The surface area of a cylinder represents the sum of the areas of its faces and is a two-dimensional measure. On the other hand, volume is a measure of the three-dimensional space occupied by the cylinder. We can calculate the surface area of a cylinder using the formula A=2πr(r+h) and we can calculate its volume using the formula V=πr²h, where r is the radius and h is the height of the cylinder.
In this article, we will learn about the surface area and volume of a cylinder. We will explore the different formulas that we can use to calculate these measurements, and we will apply them to solve some problems.
How to find the surface area of a cylinder?
To calculate the surface area of a cylinder, we have to add the areas of all the faces of the cylinder. Then, we can use the following formulas:
| $latex A_{s}=2\pi {{r}^2}+2\pi r h$ or $latex A_{s}=2\pi r(r+h)$ |
where, r is the length of the radius and h is the height of the cylinder.
Proof of the formula for the surface area of a cylinder
To prove the formula for the surface area of a cylinder, we consider the total area of a cylinder to be made up of the following parts:
- Bases area
- Curved surface area
Area of the cylinder bases
The cylinder has two circular bases, so we can calculate its area using the formula for the area of a circle. Since we have two circular bases, we multiply the formula for the area of a circle by 2:
$latex \text{Area}_{\text{bases}}=2\pi{{r}^2}$
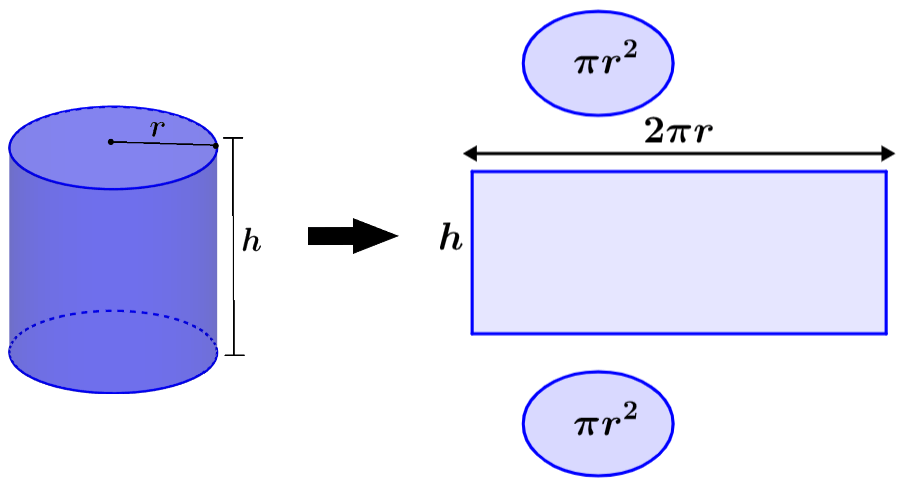
Area of the curved surface of the cylinder
The lateral surface area can be calculated using the diagram shown below. If we stretch this surface, we form a rectangle with a height of h and a base that is equal to the circumference of the circular bases, that is, 2πr.
Therefore, we can find this area with the following formula:
$latex \text{Area}_{\text{lateral}}=2\pi r h$
Total cylinder surface area
To find the total surface area of the cylinder, we have to add the area of the circular bases and the area of the lateral surface:
$latex A_{s}=2\pi {{r}^2}+2\pi r h$
or
$latex A_{s}=2\pi r(r+h)$
How to find the volume of a cylinder?
We can calculate the volume of a cylinder by multiplying the area of the base by its height:
Volume = Base × Height
Since the bases of a cylinder are circular, the area of the base is equal to πr², where r is the radius. Therefore, the formula for the volume of a cylinder is:
| $latex V=\pi {{r}^2}\times h$ |
where, r is the length of the radius of the cylinder and h is the length of its height.
Calculate the volume of a cylinder using the diameter
To calculate the volume of a cylinder using the diameter, we can use two different methods. The first method consists in dividing the diameter by 2 to get the length of the radius and applying the formula for volume shown above.
Alternatively, we can find a formula for the volume of a cylinder in terms of the diameter by substituting the expression r=d/2:
$latex V=\pi {{r}^2}\times h$
$latex V=\pi {{(\frac{d}{2})}^2}\times h$
$latex V=\pi \frac{{{d}^2}}{4}\times h$
| $latex V= \frac{\pi{{d}^2}}{4}\times h$ |
where, d is the length of the diameter.
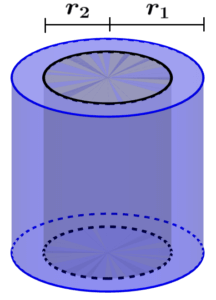
How to find the volume of a hollow cylinder
We can calculate the volume of a hollow cylinder by subtracting the volume of the hollow part from the total volume of the cylinder. This can be achieved using the following formula:
| $latex V=\pi h({{r_{1}}^2}-{{r_{2}}^2})$ |
where, $latex r_{1}$ is the radius of the cylinder, $latex r_{2}$ is the radius of the hollow part, and h is the height of the cylinder.
This formula is equivalent to calculating the volume of an entire cylinder and then extracting the volume of the inner cylinder that was removed.
Area and volume of a cylinder – Examples with answers
The formulas for the surface area and volume of a cylinder are used to solve the following examples. Try to solve the problems yourself before looking at the solution.
EXAMPLE 1
Find the surface area of a cylinder that has a radius of 5 yards and a height of 8 yards.
Solution
We have the following lengths:
- Radius, $latex r=5$
- Height, $latex h=8$
Using these lengths in the formula for the surface area, we have:
$latex A_{s}=2\pi r(r+h)$
$latex A_{s}=2\pi (5)(5+8)$
$latex A_{s}=2\pi (5)(13)$
$latex A_{s}=408.4$
The surface area is equal to 408.4 yd².
EXAMPLE 2
Find the volume of a cylinder that has a radius of 5 inches and a height of 10 inches.
Solution
We have the following:
- Radius, $latex r=5$
- Height, $latex h=10$
Applying the formula for the volume with the given lengths, we have:
$latex V=\pi {{r}^2}\times h$
$latex V=\pi {{(5)}^2}\times 10$
$latex V=\pi (25)\times 10$
$latex V=785.4$
The volume is equal to 785.4 in³.
EXAMPLE 3
What is the surface area of a cylinder that has a height of 7 feet and a radius of 6 feet?
Solution
We have the following:
- Radius, $latex r=6$
- Height, $latex h=7$
Using these values in the formula for the surface area, we have:
$latex A_{s}=2\pi r(r+h)$
$latex A_{s}=2\pi (6)(6+7)$
$latex A_{s}=2\pi (6)(13)$
$latex A_{s}=490.1$
The surface area is equal to 490.1 ft².
EXAMPLE 4
Find the volume of a cylinder that has a radius of 6 inches and a height of 8 inches.
Solution
We have the following lengths:
- Radius, $latex r=6$
- Height, $latex h=8$
Using the formula for the volume with these lengths, we have:
$latex V=\pi {{r}^2}\times h$
$latex V=\pi {{(6)}^2}\times 8$
$latex V=\pi (36)\times 8$
$latex V=904.8$
The volume is equal to 904.8 in³.
EXAMPLE 5
What is the surface area of a cylinder that has a height of 12 yards and a radius of 8 yards?
Solution
We have the following lengths:
- Radius, $latex r=8$
- Height, $latex h=12$
Using the formula for the surface area, we have:
$latex A_{s}=2\pi r(r+h)$
$latex A_{s}=2\pi (8)(8+12)$
$latex A_{s}=2\pi (8)(20)$
$latex A_{s}=1005.3$
The surface area is equal to 1005.3 yd².
EXAMPLE 6
Find the volume of a cube that has a diameter of 8 inches and a height of 12 inches.
Solution
We have the following lengths:
- Diameter, $latex d=8$
- Height, $latex h=12$
In this case, we have the length of the diameter, so we use the formula for volume in terms of the diameter of the cylinder:
$latex V=\pi (\frac{{{d}^2}}{4})\times h$
$latex V=\pi (\frac{{{(8)}^2}}{4})\times 12$
$latex V=\pi (\frac{64}{4})\times 12$
$latex V=\pi (16)\times 12$
$latex V=603.2$
The volume is equal to 603.2 in³.
EXAMPLE 7
What is the surface area of a cylinder that has a diameter of 6 feet and a height of 7 feet?
Solution
Since we have the length of the diameter, we can simply divide the diameter by 2 to get the radius of the cylinder. Therefore, we have:
- Radius, $latex r=3$
- Height, $latex h=7$
Applying the surface area formula, we have:
$latex A_{s}=2\pi r(r+h)$
$latex A_{s}=2\pi (3)(3+7)$
$latex A_{s}=2\pi (3)(10)$
$latex A_{s}=188.5$
The surface area is equal to 188.5 ft².
EXAMPLE 8
Find the volume of a cylinder that has a diameter of 12 feet and a height of 11 feet.
Solution
We have the following:
- Diameter, $latex d=12$
- Height, $latex h=11$
Using the formula for volume in terms of diameter, we have:
$latex V=\pi (\frac{{{d}^2}}{4})\times h$
$latex V=\pi (\frac{{{(12)}^2}}{4})\times 11$
$latex V=\pi (\frac{144}{4})\times 11$
$latex V=\pi (36)\times 11$
$latex V=1244.1$
The volume is equal to 1244.1 ft³.
EXAMPLE 9
Find the surface area of a cylinder that has a diameter of 12 inches and a height of 13 inches.
Solution
We can divide the diameter by 2 to get the radius, and we have:
- Radius, $latex r=6$
- Height, $latex h=13$
Using the surface area formula with the given values, we have:
$latex A_{s}=2\pi r(r+h)$
$latex A_{s}=2\pi (6)(6+13)$
$latex A_{s}=2\pi (6)(19)$
$latex A_{s}=716.3$
The surface area is equal to 716.3 in².
EXAMPLE 10
What is the volume of a hollow cylinder that has a height of 15 inches, an internal radius of 5 inches, and an external radius of 6 inches?
Solution
We have the following lengths:
- Height, $latex h=15$
- External radius, $latex r_{1}=6$
- Internal radius, $latex r_{2}=5$
Using the formula for the volume of a hollow cylinder, we have:
$latex V=\pi h({{r_{1}}^2}-{{r_{2}}^2})$
$latex V=\pi (15)({{6}^2}-{{5}^2})$
$latex V=\pi (15)(36-25)$
$latex V=\pi (15)(11)$
$latex V=518.4$
The volume is equal to 518.4 in³.
Area and volume of a cylinder – Practice problems
Solve the following problems using the different formulas for the area and volume of a cylinder. You can use the solved examples above as a guide.
See also
Interested in learning more about the area and volume of geometric figures? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
