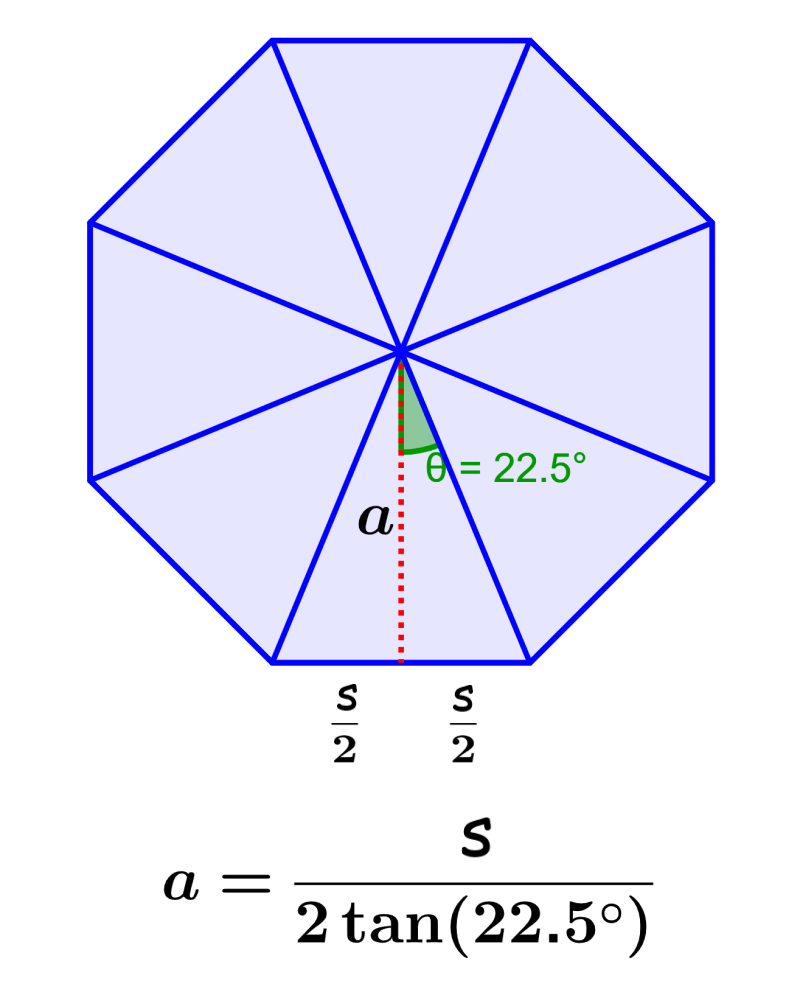
The apothem of any polygon is equal to the line that connects the center of the polygon with one of its sides perpendicularly. Using the apothem, we can calculate the area of the polygons in an easier way. We can find a formula for the apothem of an octagon by dividing the octagon into eight congruent triangles and using trigonometry to determine the height of one of the triangles since it is equivalent to the apothem.
Here, we will derive a formula for the octagon apothem using trigonometry. In addition, we will apply this formula to solve some problems.
Formula to find the apothem of an octagon
We can find a formula for the apothem of an octagon using trigonometry. For this, we start by dividing the octagon into eight congruent triangles:
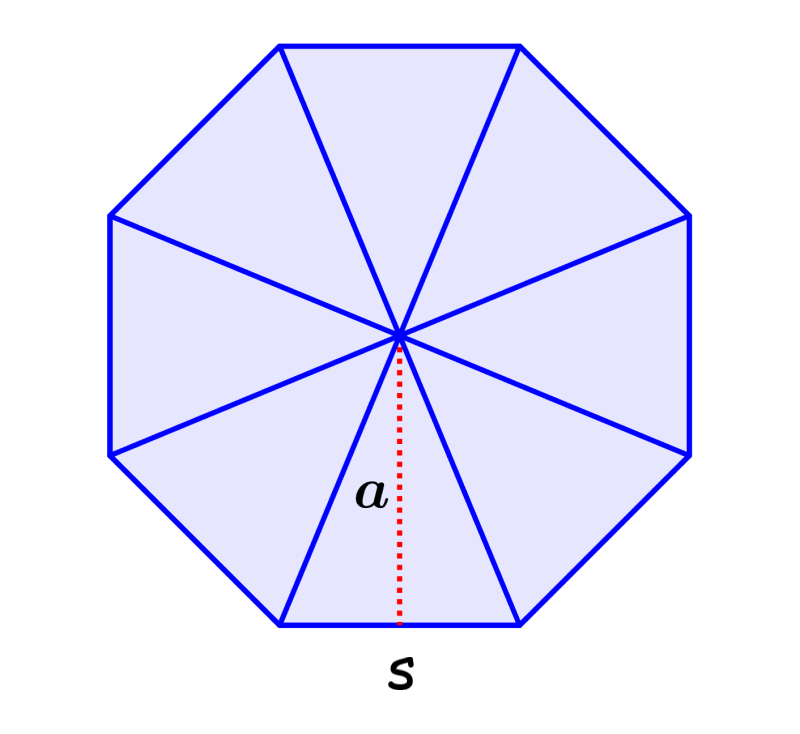
We see that the apothem divides the triangle into two small right triangles. We can see that the height of the triangle is equal to the apothem, so we can find an expression for the apothem using trigonometry. We need to find the measure of the central angle of one of the right triangles.
We know that the central angle of the octagon is equal to 360°. Also, we know that we have 16 small right triangles, so the central angle of each is $latex 360 \div 16=22.5$°:
Now that we have the angle, we can use the tangent function, which tells us that the tangent of the angle is equal to the opposite side over the adjacent side. Therefore, we have:
$$\tan(22.5)=\frac{\text{opposite}}{\text{adjacent}}$$
$$\tan(22.5)=\frac{\frac{s}{2}}{a}$$
$$\tan(22.5)=\frac{s}{2a}$$
| $$a=\frac{s}{2\tan(22.5)}$$ |
Apothem of an octagon – Examples with answers
The octagon apothem formula is used to solve the following examples. Each example has its respective solution, but it is recommended that you try to solve the exercises yourself first.
EXAMPLE 1
An octagon has sides of length 4 m. What is its apothem?
Solution
Using the apothem formula with length $latex s = 4$, we have:
$latex a=\frac{s}{2\tan(22.5°)}$
$latex a=\frac{4}{2\tan(22.5°)}$
$latex a=\frac{4}{0.828}$
$latex a=4.83$
The length of the apothem is 4.83 m.
EXAMPLE 2
What is the length of the apothem of an octagon that has sides of length 5 m?
Solution
In this case, we have the length $latex s = 5$, so we use the formula with this value:
$latex a=\frac{s}{2\tan(22.5°)}$
$latex a=\frac{5}{2\tan(22.5°)}$
$latex a=\frac{5}{0.828}$
$latex a=6.04$
The length of the apothem is 6.04 m.
EXAMPLE 3
An octagon has sides of length 9 m. What is its apothem?
Solution
We can use the apothem formula with length $latex s = 9$. Therefore, we have:
$latex a=\frac{s}{2\tan(22.5°)}$
$latex a=\frac{9}{2\tan(22.5°)}$
$latex a=\frac{9}{0.828}$
$latex a=10.87$
The length of the apothem is 10.87 m.
EXAMPLE 4
An octagon has an apothem of the length of 11.5 m. What is the length of its sides?
Solution
Here, we start with the length of the apothem and want to find the length of the sides. Therefore, we use the apothem formula with $latex a=11.5$ and solve for s:
$latex a=\frac{s}{2\tan(22.5°)}$
$latex 11.5=\frac{s}{2\tan(22.5°)}$
$latex 11.5=\frac{s}{0.828}$
$latex s=11.5(0.828)$
$latex s=9.52$
The length of the sides of the octagon is 9.52 m.
EXAMPLE 5
What is the length of the sides of an octagon that has an apothem of length 15 m?
Solution
Again, we use the apothem formula with $latex a=15$ and solve for s:
$latex a=\frac{s}{2\tan(22.5°)}$
$latex 15=\frac{s}{2\tan(22.5°)}$
$latex 15=\frac{s}{0.828}$
$latex s=15(0.828)$
$latex s=12.42$
The length of the sides of the octagon is 12.42 m.
Apothem of an octagon – Practice problems
Put into practice the use of the apothem formula to solve the following problems. If you need help with this, you can look at the solved examples above.
See also
Interested in learning more about octagons? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
