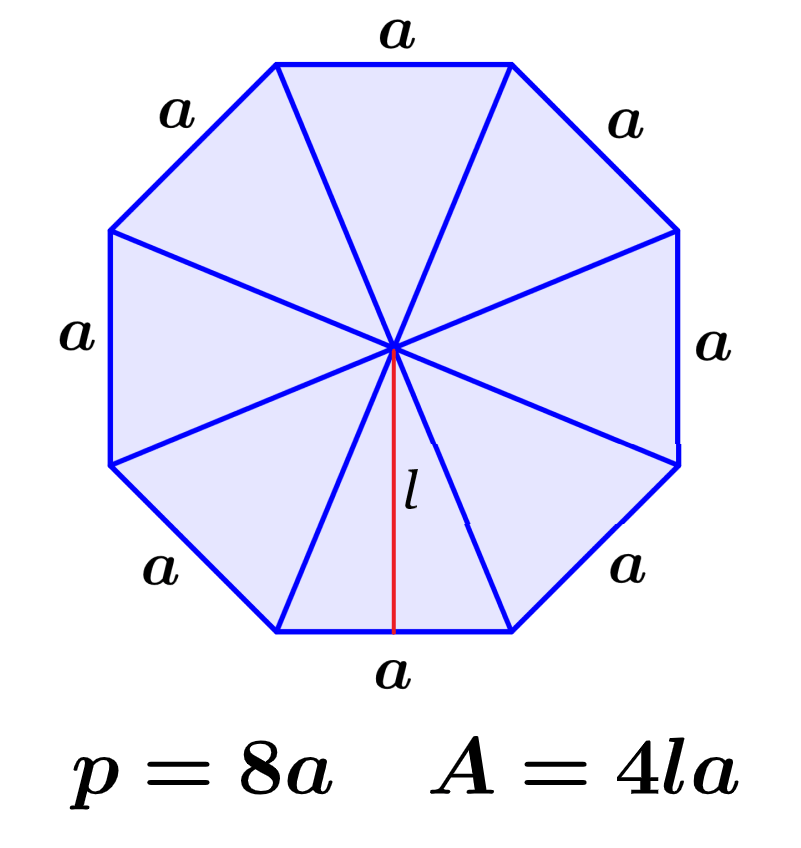
The perimeter of an octagon is the total length around its outline. On the other hand, the area is a measure of the two-dimensional space occupied by the figure. We can calculate the perimeter of an octagon by adding the lengths of its eight sides and we can calculate its area by multiplying by four the product of one of its sides and its apothem.
In this article, we will learn all about the perimeter and area of an octagon. We will explore its formulas and apply them to solve some practice problems.
How to find the perimeter of an octagon?
To calculate the perimeter of an octagon, we have to add the lengths of its eight sides. Therefore, we can use the following formula:
$$p=a+b+c+d+e+f+g+h$$
where, $latex a,~b,~c,~d,~e,~f,~g,~h$ are the lengths of the eight sides of the octagon.
Also, if we have a regular octagon, we know that the lengths of its eight sides are the same, so we can multiply the length of one of its sides by eight to find the perimeter:
| $latex p=8a$ |
where, a is the length of one of the sides of the regular octagon.
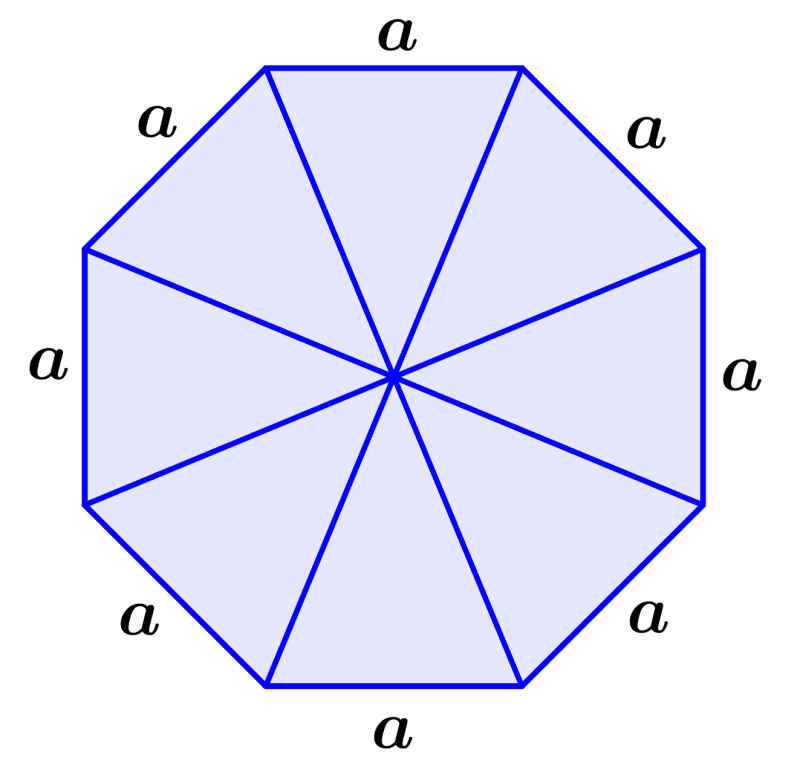
How to find the area of an octagon?
To calculate the area of an octagon, we can multiply by 4 the product of the length of one of its sides and its apothem. Therefore, we can use the following formula:
| $latex A=4sa$ |
where, s is the length of one of the sides of the octagon and a is the length of the apothem.
Proof of the formula for the area of an octagon
The area of any polygon can be found by dividing it into congruent triangles and calculating the area of each triangle. In the case of octagons, we can divide the figure into eight congruent triangles, as shown below:
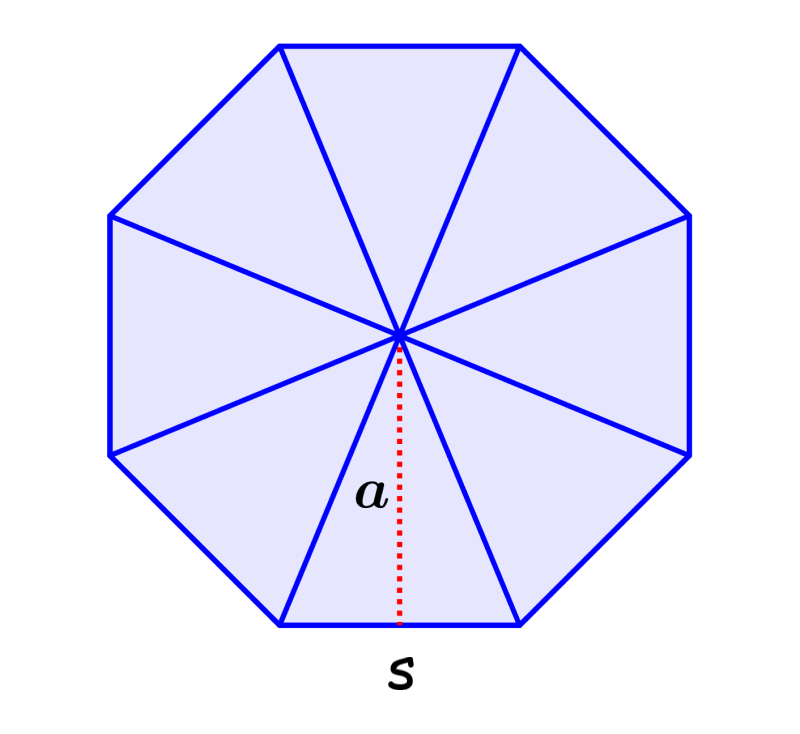
Now, we recall that the area of any triangle can be calculated using the formula $latex A=\frac{1}{2}bh$, where b is the length of the base and h is the length of the height.
In the diagram, we can see that the height of the triangle is equal to the apothem of the octagon and the base of the triangle is equal to the length of one of its sides, so we have $latex A=\frac{1}{2} sa$.
Since we have eight congruent triangles, we can multiply by eight to get the following formula:
$latex A=4sa$
Find the area of an octagon without using the apothem
We can calculate the area of a regular octagon without using the length of its apothem. For this, we can obtain a formula for the area of a regular octagon only in terms of its sides.
Using trigonometry and simplifying, we can find the following formula:
| $latex A=2(1+\sqrt{2}){{s}^2}$ |
where, s is the length of one of the sides of the octagon.
Area and perimeter of an octagon – Examples with answers
EXAMPLE 1
What is the perimeter of a regular octagon that has sides with a length of 5 inches?
Solution
Applying the formula for the perimeter with the length $latex a=5$, we have:
$latex p=8a$
$latex p=8(5)$
$latex p=40$
The perimeter of the octagon is equal to 40 in.
EXAMPLE 2
Find the area of a regular octagon that has sides with a length of 5 inches and an apothem with a length of 6.04 inches.
Solution
We have the following lengths:
- Sides, $latex s=5$ in
- Apothem, $latex a=6.04$ in
Using these lengths in the area formula, we have:
$latex A=4la$
$latex A=4(5)(6.04)$
$latex A=120.8$
The area of the octagon is equal to 120.8 in².
EXAMPLE 3
What is the perimeter of a regular octagon that has sides with a length of 8 feet?
Solution
Using the length $latex a=8$ in the formula for the perimeter of the octagon, we have:
$latex p=8a$
$latex p=8(8)$
$latex p=64$
The perimeter of the octagon is equal to 64 ft.
EXAMPLE 4
Find the area of a regular octagon that has sides with a length of 6 inches and an apothem of 7.24 inches.
Solution
We have the following:
- Sides, $latex s=6$ in
- Apothem, $latex a=7.24$ in
Using these lengths in the formula for the area, we have:
$latex A=4sa$
$latex A=4(6)(7.24)$
$latex A=173.76$
The area of the octagon is equal to 173.76 in².
EXAMPLE 5
Find the perimeter of a regular octagon that has sides with a length of 15 inches.
Solution
We have the length $latex a=15$. Using this value in the perimeter formula, we have:
$latex p=8a$
$latex p=8(15)$
$latex p=120$
The perimeter of the octagon is equal to 120 in.
EXAMPLE 6
Find the area of a regular octagon that has sides with a length of 11 feet and an apothem with a length of 13.28 feet.
Solution
We have the following lengths:
- Sides, $latex s=11$ ft
- Apothem, $latex a=13.28$ ft
Applying these values in the formula for the area, we have:
$latex A=4sa$
$latex A=4(11)(13.28)$
$latex A=584.32$
The area of the octagon is equal to 584.32 ft².
EXAMPLE 7
Find the length of the sides of a regular octagon that has a perimeter of 112 yards.
Solution
In this case, we know the perimeter of the octagon, and we want to find the length of the sides of the octagon. Therefore, we use the formula for the perimeter and solve for a:
$latex p=8a$
$latex 112=8a$
$latex a=14$
The length of the sides of the octagon is 14 yd.
EXAMPLE 8
Find the area of a regular octagon that has sides with a length of 8 feet.
Solution
In this case, we only have the length of one side of the octagon, so we can use the second formula for the area with $latex s=8$:
$latex A=2(1+\sqrt{2}){{s}^2}$
$latex A=2(1+\sqrt{2}){{(8)}^2}$
$latex A=2(1+\sqrt{2})(64)$
$latex A=309.02$
The area of the octagon is equal to 309.02 ft².
EXAMPLE 9
What is the length of the sides of a regular octagon that has a perimeter of 152 inches?
Solution
Using the formula for the perimeter with $latex p=152$ and solving for a, we have:
$latex p=8a$
$latex 152=8a$
$latex a=19$
The length of the sides of the octagon is equal to 19 in.
EXAMPLE 10
Find the area of a regular octagon that has sides with a length of 10 yards.
Solution
We can use the second area formula with $latex s=10$:
$latex A=2(1+\sqrt{2}){{s}^2}$
$latex A=2(1+\sqrt{2}){{(10)}^2}$
$latex A=2(1+\sqrt{2})(100)$
$latex A=482.84$
The area of the octagon is equal to 482.84 yd².
Area and perimeter of an octagon – Practice problems
See also
Interested in learning more about perimeters and areas of geometric figures? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
