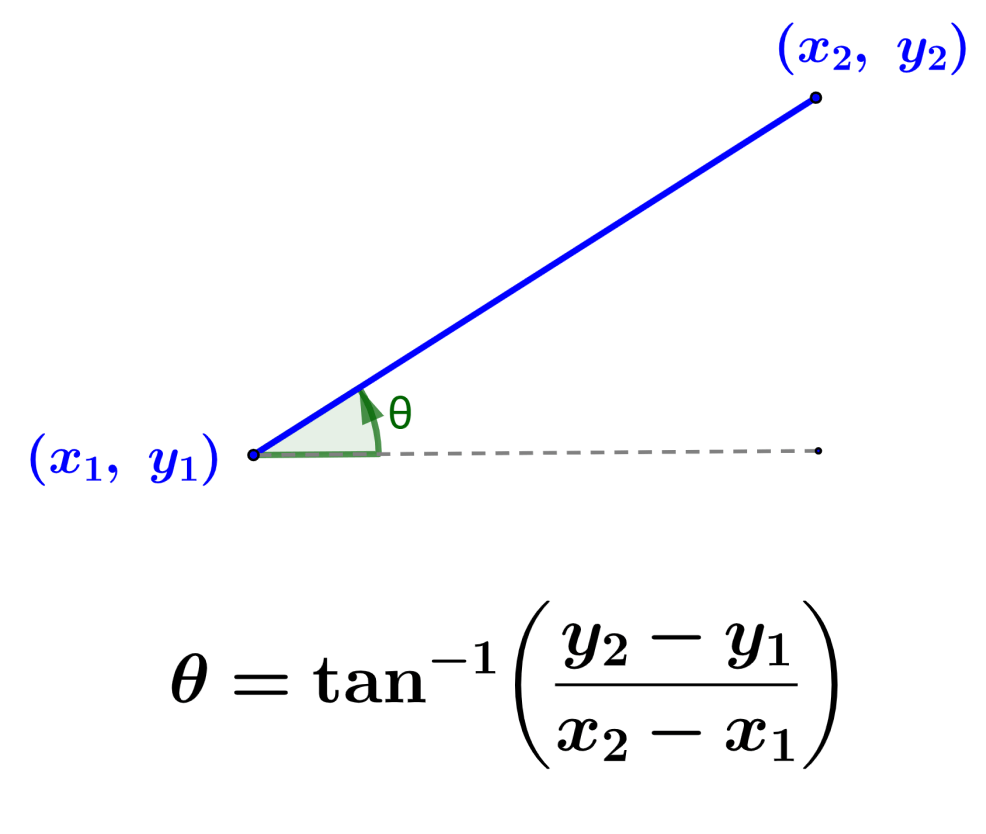The angle of inclination of a line or the angle of the slope of the line is the angle formed by the line and its horizontal component. To get the value of this angle, we have to use trigonometry, specifically the tangent function. The angle can be positive or negative depending on the direction in which it is measured.
Here, we will learn how to calculate the angle of slope of a line. We will look at its formula, some important considerations, and several examples with answers.
Formula for the angle of slope of a line
To find the formula for the angle of inclination or slope of a straight line, we are going to use the following diagram:
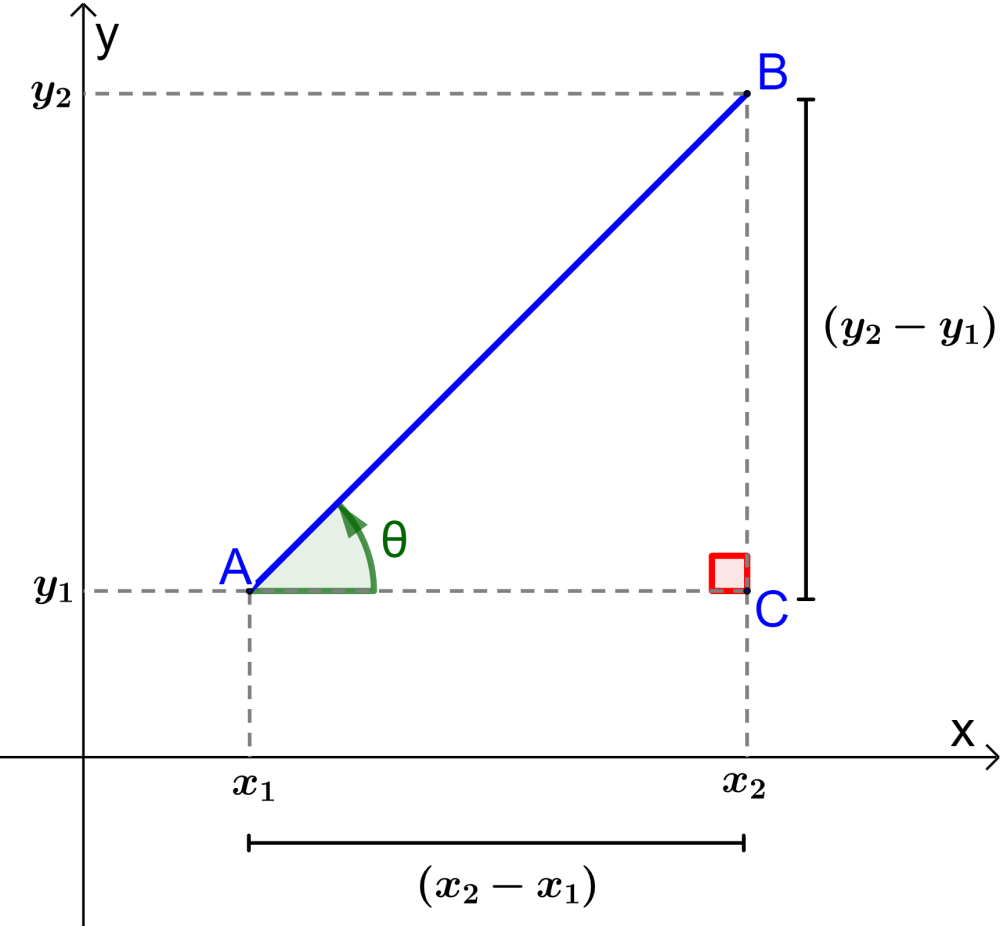
We can see that the diagram has a right triangle ABC formed by the horizontal and vertical components of the line. In the diagram, θ is the angle formed by line AB and its horizontal component.
Using trigonometry and recalling that the tangent of an angle is equal to the opposite side over the adjacent side, we have $latex \tan(\theta)=\frac{BC}{AC}$.
Now, using the diagram, we can see that $latex \frac{BC}{AC}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$, which is equal to the slope of line AB.
Therefore, we have the following:
$$\tan(\theta)=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$$
$$\theta=\tan^{-1}\left(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\right)$$
Important remarks:
- If $latex m$ is the slope of line AB, then the angle of the slope of the line is equal to $latex \tan^{-1}(m)$.
- When the result of $latex \tan^{-1}(m)$ is negative, the angle θ is measured from the horizontal line to the straight line in a clockwise direction.
Angle of slope of a line – Examples with answers
The formula for the angle of the slope of a straight line is used to solve the following examples. Try to solve the problems yourself before looking at the solution.
EXAMPLE 1
Find the angle formed by the line that has the points A=(-7, -5) and B=(5, -3) with respect to the horizontal.
Solution
Obtaining a simple graph, we have:
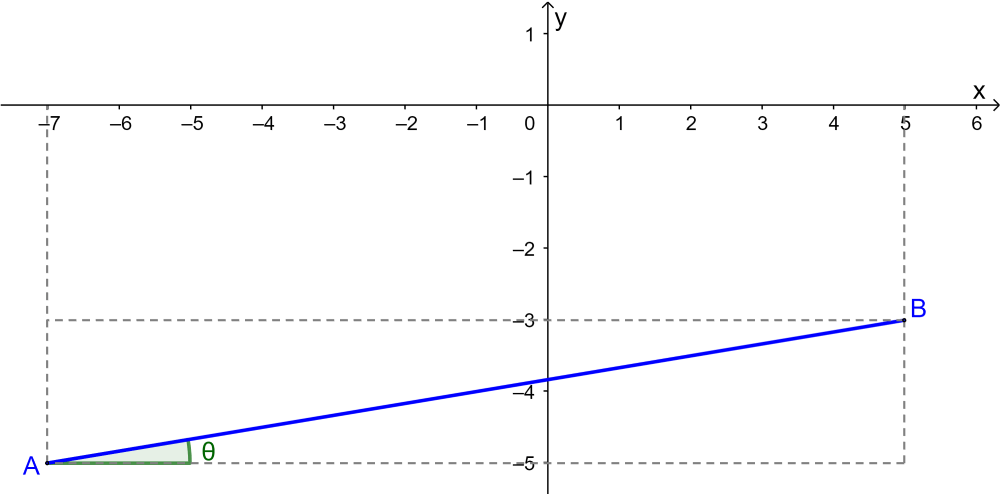
To find the angle θ, we are going to use the formula for the angle of the slope of a straight line:
$$\theta=\tan^{-1}\left(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\right)$$
$$=\tan^{-1}\left(\frac{-3-(-5)}{5-(-7)}\right)$$
$$=\tan^{-1}\left(\frac{-3+5}{5+7}\right)$$
$$=\tan^{-1}\left(\frac{2}{12}\right)$$
$$=\tan^{-1}\left(\frac{1}{6}\right)$$
$$\theta=9.46^{\circ}$$
EXAMPLE 2
Find the angle of slope of the line that has points A=(5, -4) and B=(-6, 7).
Solution
We can find the angle θ, by using the formula for the angle of inclination of a line with the coordinates of the two given points:
$$\theta=\tan^{-1}\left(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\right)$$
$$=\tan^{-1}\left(\frac{7-(-4)}{-6-5}\right)$$
$$=\tan^{-1}\left(\frac{7+4}{-6-5}\right)$$
$$=\tan^{-1}\left(\frac{11}{-11}\right)$$
$$=\tan^{-1}\left(-1\right)$$
$$\theta=-45^{\circ}$$
EXAMPLE 3
A line passes through the points A=(7, -2) and B=(3, -5). Find the angle of the slope of AB.
Solution
Let’s find the angle θ using the formula for the angle of slope of a line with the coordinates of the given points:
$$\theta=\tan^{-1}\left(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\right)$$
$$=\tan^{-1}\left(\frac{-5-(-2)}{3-7}\right)$$
$$=\tan^{-1}\left(\frac{-5+2}{3-7}\right)$$
$$=\tan^{-1}\left(\frac{-3}{-4}\right)$$
$$=\tan^{-1}\left(\frac{3}{4}\right)$$
$$\theta=36.9^{\circ}$$
EXAMPLE 4
Determine the angle of the slope of the line that passes through the points A=(6, 7) and B=(12, 7).
Solution
Using the coordinates of the points in the formula for the angle of slope, we have:
$$\theta=\tan^{-1}\left(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\right)$$
$$=\tan^{-1}\left(\frac{7-7}{12-6}\right)$$
$$=\tan^{-1}\left(\frac{0}{6}\right)$$
$$\theta=0^{\circ}$$
We got an angle equal to 0°. This means that the line is horizontal.
Looking at the y-coordinates of both points, we see that they are the same. This only happens when a line is horizontal.
EXAMPLE 5
Find the angle of the slope of the line that passes through the points A=(3, 7) and B=(-6, 11).
Solution
We can find the angle of the slope by using the formula with the coordinates of the given points:
$$\theta=\tan^{-1}\left(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\right)$$
$$=\tan^{-1}\left(\frac{11-7}{-6-3}\right)$$
$$=\tan^{-1}\left(-\frac{4}{9}\right)$$
$$\theta=-24^{\circ}$$
EXAMPLE 6
Find the angle formed by the line that passes through the points A=(5, -3) and B=(5, 2).
Solution
To find the angle θ, we use the coordinates of the given points in the formula for the angle of a slope:
$$\theta=\tan^{-1}\left(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\right)$$
$$=\tan^{-1}\left(\frac{2-(-3)}{5-5}\right)$$
$$=\tan^{-1}\left(\frac{-2-3}{5-5}\right)$$
$$=\tan^{-1}\left(\frac{-5}{0}\right)$$
$$=\tan^{-1}\left(\text{infinito}\right)$$
$$\theta=90^{\circ}$$
In this case, we got -5/0, which is equal to infinity. Looking at the x-coordinates of both points, we see that they are both equal to 5. This only happens when we have a vertical line.
A vertical line is perpendicular to the horizontal, so the angle is equal to 90°.
Angle of slope of a line – Practice problems
Use the formula for the angle of inclination or slope of a line to solve the following practice problems.
See also
Interested in learning more about lines? You can take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
